Matematyka

Częściowe właściwości pochodne, obliczenia, ćwiczenia

Częściowe właściwości pochodne, obliczenia, ćwiczenia

częściowe pochodne funkcji z kilkoma zmiennymi niezależnymi są te, które są osiągane przez przyjmowanie zwykłej pochodnej w jednej ze zmiennych, podczas gdy inne są utrzymywane lub traktowane jako stałe.

Pochodna częściowa w jednej ze zmiennych określa, w jaki sposób funkcja zmienia się w każdym punkcie, na jednostkę zmiany danej zmiennej. 

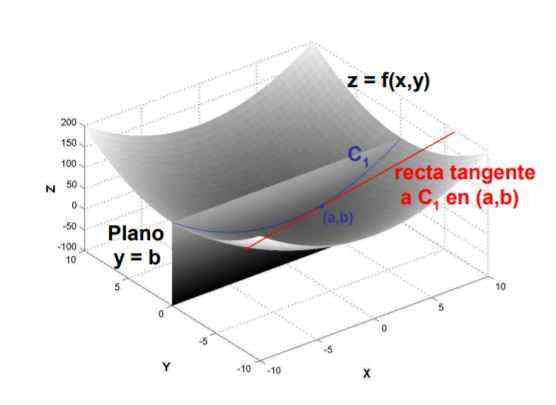Rysunek 1. Nachylenie linii stycznej do krzywej utworzonej przez przecięcie płaszczyzny y = b z powierzchnią f (x, y) w punkcie (a, b) jest częściową pochodną f w odniesieniu do x, oceniana w tym momencie. Źródło: UPM.Jest

Ze względu na jego definicję, częściowa pochodna jest obliczana przy użyciu matematycznej granicy ilorazu między zmiennością funkcji a zmiennością zmienną w odniesieniu do tego, co jest wyprowadzone, gdy zmiana tego ostatniego dąży do zera.

Załóżmy, że przypadek funkcji F To zależy od zmiennych X I I, to znaczy dla każdej pary (X, y) A jest przypisane z: 

f: (x, y) → z .

Częściowa pochodna funkcji Z = f (x, y), w szacunku dla X jest definiowany jako:

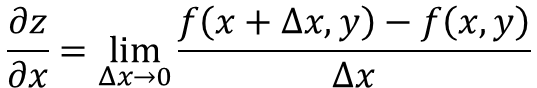
Teraz istnieje kilka sposobów oznaczenia częściowej pochodnej funkcji, na przykład:

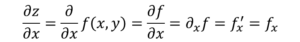
Różnica w stosunku do zwykłej pochodnej pod względem notacji polega na tym, że D wyprowadzenia jest zmieniane na symbol ∂, znany jako „Jacobi D”.

[TOC]

Właściwości częściowych pochodnych

Częściowa pochodna funkcji kilku zmiennych, w odniesieniu do jednej z nich, jest zwykłą pochodną we wspomnianej zmiennej i biorąc pod uwagę resztę jako ustalone lub stałe. Aby znaleźć częściową pochodną, ​​można zastosować zasady pochodzenia zwykłych pochodnych.

Poniżej głównych właściwości:

Może ci służyć: wspólny czynnik grupowania warunków: przykłady, ćwiczenia

Ciągłość

Jeśli funkcja f (x, y) ma częściowe pochodne w X I I o punkcie (Xo, ja) Następnie można powiedzieć, że funkcja jest w tym momencie ciągła.

Zasada łańcuchowa

Funkcja f (x, y) Z ciągłymi częściowymi pochodnymi w X I I, Co z kolei zależy od parametru T Poprzez x = x (t) I y = y (t), Ma zwykłą pochodną w odniesieniu do zmiennej T, który jest obliczany przez zasadę łańcucha:

DT Z = ∂XZ dTx + ∂IZ dTI

Zamknięcie lub blokada właściwości

Częściowa pochodna w odniesieniu do jednej ze zmiennych funkcji F dwóch lub więcej zmiennych (X, y, ...), To kolejna funkcja G Na przykład w tych samych zmiennych: 

G (x, y, ...) = ∂I f (x, y, ...)

Oznacza to, że częściowe wyprowadzenie jest operacją wynikającą z RN RN. W tym sensie mówi się, że jest to Operacja zamknięta.

Kolejne częściowe pochodne

Można zdefiniować kolejne częściowe pochodne funkcji kilku zmiennych, co daje nowe funkcje w tych samych zmiennych niezależnych.

Być funkcją f (x, y). Można zdefiniować następujące kolejne pochodne:

FXx = ∂XF ;  FTak = ∂TakF ; FXy = ∂XyF I FYx = ∂YxF

Dwa ostatnie są znane jako Mieszane pochodne ponieważ obejmują dwie różne zmienne niezależne.

Twierdzenie Schwarz

Być funkcją f (x, y), zdefiniowane w taki sposób, że jego częściowe pochodne są funkcjami ciągłymi w otwartym podzbiorze R2.

Tak więc dla każdej pary (X, y) Że należą do wspomnianego podzbioru, mieszane pochodne są identyczne:

∂XyF = ∂YxF

Poprzednie stwierdzenie jest znane jako Twierdzenie Schwarz.

Jak obliczane są częściowe pochodne?

Pochodne częściowe są obliczane podobnie do pierwotnych funkcji pochodnych w jednej zmiennej niezależnej. Gdy podejmowana jest częściowa pochodna funkcji kilku zmiennych w odniesieniu do jednej z nich, pozostałe zmienne są traktowane jako stałe.

Może ci służyć: połowa 15

Poniżej znajduje się kilka przykładów:

Przykład 1

Być funkcją:

f (x, y) = -3x2 + 2 (i - 3)2

Należy obliczyć pierwszą częściową pochodną w odniesieniu do X i pierwsza częściowa pochodna w odniesieniu do I.

Procedura

Aby obliczyć częściowe F w szacunku dla X, Jest zajęty I jako stałe:

∂XF = ∂X(-3x2 + 2 (i - 3)2 ) = ∂X(-3x2 )+ ∂X(2 (i - 3)2 ) = -3 ∂X(X2) + 0 = -6x.

I z kolei, aby obliczyć pochodną w odniesieniu do I Jest zajęty X jako stałe:

∂IF = ∂I(-3x2 + 2 (i - 3)2 ) = ∂I(-3x2 )+ ∂I(2 (i - 3)2 ) = 0 + 2 · 2 (y - 3) = 4Y - 12.

Przykład 2

Określ częściowe pochodne drugiego rzędu:  ∂Xxf, ∂Takf, ∂YxF I ∂XyF Dla tej samej funkcji F przykład 1.

Procedura

W tym przypadku, ponieważ pierwsza pochodna częściowa jest już obliczona X I I (Patrz przykład 1):

∂XxF = ∂X(∂Xf) = ∂X(-6x) = -6

∂TakF = ∂I(∂If) = ∂I(4Y - 12) = 4

∂YxF = ∂I(∂Xf) = ∂I(-6x) = 0

∂XyF = ∂X(∂If) = ∂X(4Y - 12) = 0

Obserwuje się, że ∂YxF = ∂XyF, w ten sposób spełniając twierdzenie Schwarza, ponieważ funkcja F a jego pierwsza częściowe pochodne są wszystkie funkcje ciągłe w R2.

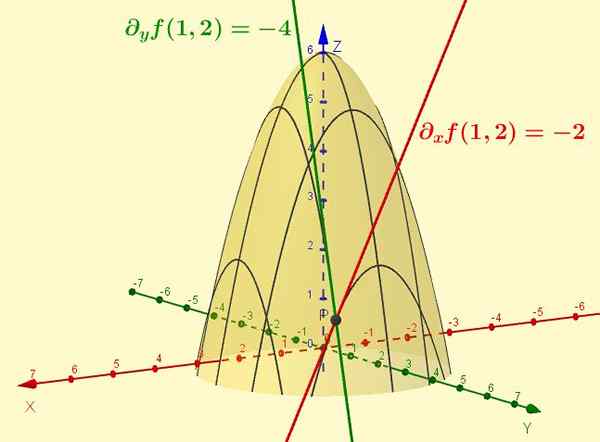
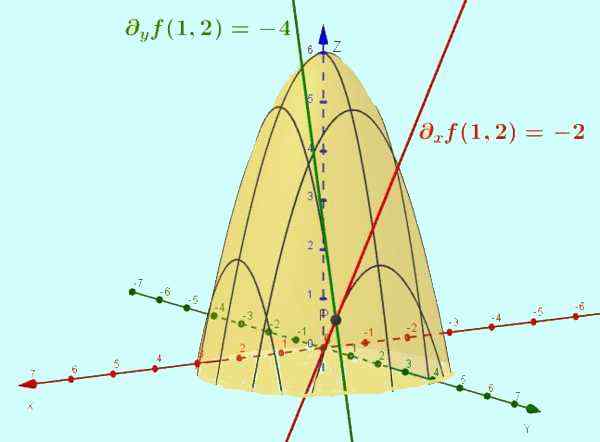Rysunek 2. Funkcja z = f (x, y) = -x2 - y2 + 6 jest powierzchnią pokazaną na rysunku. Częściowa pochodna w odniesieniu do x jest nachyleniem stycznej linii krzywej, która wynika z przecięcia wspomnianej powierzchni z płaszczyzną y = ctte (konkretny przypadek jest pokazany y = 2). Podobnie część F w odniesieniu do i jest nachyleniem stycznej do przecięcia z x = 1, w punkcie (1, 2, 1).

Rozwiązane ćwiczenia

Ćwiczenie 1

Być funkcją:

Może ci służyć: kwadratowe sukcesy: przykłady, reguły i ćwiczenia rozwiązane

f (x, y) = -x2 - I2 + 6

Znajdź funkcje G (x, y) = ∂XF  I H (x, y) = ∂IF.

Rozwiązanie

Częściowa pochodna F w szacunku dla X, dla którego zmienna I Staje się stały:

G (x, y) = - 2x

Podobnie częściowa pochodna G w szacunku dla I, czyn X stałe, w wyniku czego funkcja H:

H (x, y) = -2y

Ćwiczenie 2 

Oceń punkt (1, 2) funkcje f (x, y) I G (x, y) ćwiczenia 1. Interpretuj wyniki.

Rozwiązanie

Wartości są zastąpione x = 1 I y = 2 Uzyskanie:

f (1,2) = -(1)2 -(2)2 + 6 = -5 + 6 = 1

Jest to wartość, która przyjmuje funkcję F, gdy jest oceniana w tym momencie.

Funkcja f (x, y) Jest to dwukenowa powierzchnia i współrzędna Z = f (x, y) Jest to wysokość funkcji dla każdej pary (X, y). Kiedy para jest zajęta (1.2), Wysokość powierzchni f (x, y) Jest Z = 1.

Funkcja G (x, y) = - 2x reprezentuje płaszczyznę w trójwymiarowej przestrzeni, której równanie jest Z = -2x O Cóż -2x + 0 i -z = 0.

Wspomniany samolot jest prostopadły do ​​samolotu Xz I przejdź przez punkt (0, 0, 0). Oceniona w x = 1 I y = 2 Więc Z = -2. Zauważ, że wartość Z = g (x, y) Jest niezależny od wartości przypisanej do zmiennej I.

Z drugiej strony, jeśli powierzchnia przecina się f (x, y) Z samolotem y = c, z C stałe, masz krzywą w płaszczyźnie ZX: Z = -x2 - C2 + 6.

W tym przypadku pochodna z w szacunku dla X pokrywa się z częściową pochodną f (x, y) w szacunku dla X: DX Z = ∂XF .

Podczas oceny w pary (x = 1, y = 2) Częściowa pochodna w tym momencie ∂XF (1.2) Jest interpretowany jako nachylenie stycznej linii do krzywej Z = -x2 + 2 o punkcie (x = 1, y = 2) A wartość tego nachylenia jest -2.

Bibliografia

  1. Ayres, f. 2000. Obliczenie. 5Ed. MC Graw Hill.
  2. Częściowe pochodne funkcji w kilku zmiennych. Odzyskane z: Building.UPM.Jest.
  3. Leithold, L. 1992. Obliczanie za pomocą geometrii analitycznej. Harla, s.DO.
  4. Purcell, e. J., Varberg, d., & Rigdon, s. I. (2007). Obliczenie. Meksyk: Pearson Education.
  5. Gorostizaga J. C. Częściowe pochodne. Odzyskane z: ehu.EUS
  6. Wikipedia. Częściowa pochodna. Odzyskane z: jest.Wikipedia.com.