Instrumenty domyślne sposób ich rozwiązania i rozwiązania ćwiczeń

Instrumenty domyślne Są to narzędzia stosowane w technice różnicowania zastosowanej do funkcji. Obowiązują, gdy nie jest to możliwe, zgodnie z regularnymi metodami, wykonują prześwit zmiennej zależnej, która ma na celu wyprowadzenie. Ten prześwig odbywa się na podstawie zmiennej niezależnej.

Na przykład w wyrażeniu 3xy³ - 2Y + XY² = xy, nie możesz uzyskać wyrażenia, które określa „y” w zależności od „x”. Tak że gdy można uzyskać różnicową ekspresję/dx.

[TOC]

W jaki sposób rozstrzygane są niejawne pochodne?

Aby rozwiązać implikację, opiera się ono na wyrażeniu ukrytym. Na przykład: 3xy³ - 2Y + XY² - Xy = 0. Zostało to już jasno oczyszczone, jednak nie jest to warunek niezbędny do uzyskania pochodnej y w odniesieniu do x. Następnie każdy z elementów jest wyprowadzany z reguły łańcucha dla funkcji mieszanych:

3xy³ Składa się z 2 zmiennych, a zatem D (3xy³) Będzie traktowany jako pochodna produktu funkcji.

D (3xy³)/dx = 3y³ + 3y².(3x) i '= 3y³ + 9xy² I'

Gdzie element i „jest znany jako”i kuzyn”I reprezentuje DY/DX

-2y wywodzi się zgodnie z prawem k.U = k.LUB'

D (-2y) = -2 i '

Xy² przypuszcza, że ​​inny różnicowy złożony z produktu funkcji

D (xy²) = y² + 2xy i '

-Xy to homologiczny sposób

d (-xy) = -y -x i '

Są one zastąpione w równości, wiedząc, że zero pochodnej wynosi zero.

3y³ + 9xy² i „ - 2 i” + i² + 2xy i ' - y - x i' = 0

Elementy, które mają termin i „są zgrupowane razem po jednej stronie równości

Może ci służyć: wektory Colineal

3y³ + I² - y = -9xy² oraz „ + 2 i„ + x i ”

Wspólny czynnik i „we właściwym elemencie równości są wyodrębnione

3y³ + I² - y = y '(-9xy² + x + 2)

Wreszcie termin, który się mnoży i ”. Uzyskanie w ten sposób wyrażenia odpowiadające niejawnej pochodnej y w odniesieniu do x.

i '= dy/dx = (3y³ + I² - y)/(-9xy² + x + 2)

Zasada łańcuchowa

W niejawnym wyprowadzaniu reguła łańcucha jest zawsze szanowana. Wszystkie wyrażenia różnicowe zostaną podane w zależności od zmiennej niezależnej x. Tak, aby każda zmienna θ inna niż x musi zawierać termin dθ/dx po wyprowadzeniu.

Termin ten pojawi się tylko w pierwszym stopniu lub z wykładnikiem równym 1. Ta jakość wyjaśnia całkowicie w tradycyjnych metodach faktoralizacji. Tak, że możliwe jest uzyskanie wyrażenia, które definiuje różnicowy dθ/dx.

W zasadzie łańcucha pokazano postępowy charakter procesu różnicowania lub pochodnego. Gdzie dla dowolnej funkcji kompozytowej f [g (x)], różnicowa ekspresja f będzie musiała być

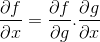
Zamówienie operacyjne

W każdej stosowanej formule lub prawa pochodnego należy wziąć pod uwagę kolejność zmiennych. Kryteria związane ze zmienną niezależną są szanowane, bez zmiany jej korelacji ze zmienną zależną.

Stosunek zmiennej zależnej w momencie wyprowadzenia jest przyjmowany bezpośrednio.; Z wyjątkiem, że zostanie to uznane za drugą funkcję, dlatego stosowane są kryteria reguły łańcuchowej dla funkcji mieszanych.

Można to opracować w wyrażeniach o więcej niż 2 zmiennych. Zgodnie z tymi samymi zasadami wszystkie różnice odnoszące się do zmiennych zależnych zostaną oznaczone.

Może ci służyć: jakie są wytyczne? (Geometria)

Zastosowane jest graficznie te same kryteria, które określają pochodną. Podczas gdy pochodna jest nachyleniem stycznej linii do krzywej w płaszczyźnie, reszta różnic należących do zmiennych zależnych (Dy/Dx, Dz/Dx) reprezentuje płaszczyzny styczne do ciał wektorowych opisanych przez funkcje wielu zmiennych.

Domniemany funkcji

Mówi się, że funkcja jest domyślnie zdefiniowana, jeśli wyrażenie y = f (x) może być reprezentowane jako funkcja wielokrotnej zmiennej f (x, y) = 0, podczas gdy f jest zdefiniowane w płaszczyźnie r².

3xy³ - 2Y + XY² = x i może być napisane w formie 3xy³ - 2Y + XY² - Xy = 0

Z uwagi na niemożność wyjaśnienia funkcji y = f (x).

Historia

Różnice różnicowe zaczęło być mianowane przez różnych badaczy matematycznych, około XVII wieku. Po raz pierwszy wspomniano o wkładach Newtona i Leibniza. Oba leczyły różniczkowy rachunek z różnych punktów widzenia, ale zbieżne w swoich wynikach.

Podczas gdy Newton skupił się na różnicowaniu jako szybkości prędkości lub zmian, podejście Leibniz było bardziej geometryczne. Można powiedzieć, że Newton zaatakował przypuszczenia pozostawione przez Apolloniusza z Perge i Leibniz geometryczne idee Fermata.

Domniemane wyprowadzenie pojawia się natychmiast, gdy rozważają równania różnicowe i kompleksowe. Rozszerzyli geometryczną koncepcję Leibniz na R³ a nawet wielowymiarowe przestrzenie.

Aplikacje

Domyślne pochodne są stosowane w różnych sytuacjach. Są one powszechne w problemach kursów walutowych między zmiennymi powiązanymi, gdzie, w zależności od poczucia badania, zmienne będą uważane za zależne lub niezależne.

Mają także interesujące zastosowania geometryczne, takie jak problemy odbicia lub cieni, na postaciach, których kształt można modelować matematycznie.

Może ci służyć: pobieranie próbek kwot: metoda, zalety, wady, przykłady

Są one często używane w obszarach gospodarki i inżynierii, a także w różnych badaniach zjawisk naturalnych i budynków eksperymentalnych.

Rozwiązane ćwiczenia

Ćwiczenie 1

Zdefiniuj niejawną ekspresję, która określa DY/DX

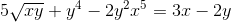
Każdy element różni się od wyrażenia

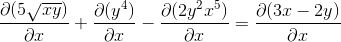
Ustanowienie zasady łańcucha w każdym kompetentnym przypadku

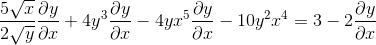
Grupowanie po jednej stronie równości elementy, które mają Dy/DX

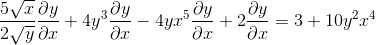
Uwzględnia wspólny czynnik

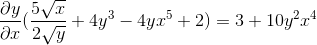
Jest usuwany przez uzyskanie poszukiwanego wyrażenia

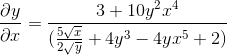
Ćwiczenie 2

Zdefiniuj niejawną ekspresję, która określa DY/DX

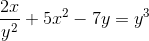
Wyrażanie pochodnych do przeprowadzenia

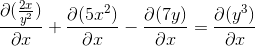
Domyślnie pochodzący zgodnie z zasadą łańcucha

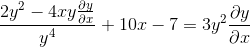
Faktoring wspólnych elementów

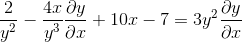
Grupowanie terminu dy/dx po jednej stronie równości

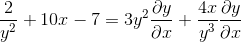
Wspólny czynnik dla elementu różnicowego

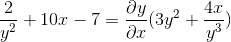
Oczyszczamy i uzyskujemy poszukiwany wyraz

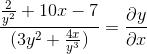
Bibliografia

1. Rachunek pojedynczej zmiennej. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 listopada. 2008
2. Twierdzenie o funkcji niejawnej: historia, teoria i aplikacje. Steven G. Krantz, Harold R. Parki. Springer Science & Business Media, 9 listopada. 2012
3. Analiza wielowymiarowa. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 grudnia. 2010
4. Dynamika systemu: modelowanie, symulacja i kontrola systemów mechatronicznych. Dean c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 marca. 2012
5. Rachunek: matematyka i modelowanie. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 stycznia. 1999