Pochodne algebraiczne

Co to są pochodne algebraiczne?

Pochodne algebraiczne Składają się one z badania pochodnej w konkretnym przypadku funkcji algebraicznych. Pochodzenie pojęcia pochodnych pochodzi z starożytnej Grecji. Rozwój tego pojęcia był motywowany potrzebą rozwiązania dwóch ważnych problemów, jednego z fizyki i jednego w matematyce.

W fizyce pochodna rozwiązuje problem określania chwilowej prędkości poruszającego się obiektu. W matematyce pozwala znaleźć linię styczną do krzywej w danym punkcie.

Chociaż naprawdę istnieje wiele innych problemów, które są rozwiązane przy użyciu pochodnej, a także jej uogólnienia, wyniki, które przyszły później do wprowadzenia ich koncepcji.

Pionierzy różnicowego rachunku to Newton i Leibniz. Przed podaniem formalnej definicji rozwiniemy ideę, z matematycznego i fizycznego punktu widzenia.

Pochodna w oczekiwaniu na linię styczną do krzywej

Załóżmy, że wykres funkcji y = f (x) jest wykresem ciągłym (bez skoków, wierzchołków lub separacji) i albo a = (a, f (a)) stały punkt nad nim. Chcemy znaleźć równanie linii stycznej z funkcją F w punkcie A.

Weźmy kolejny punkt p = (x, f (x)) wykres. Linia suszenia to linia, która przecina wykres krzywej w jeden lub więcej punktów.

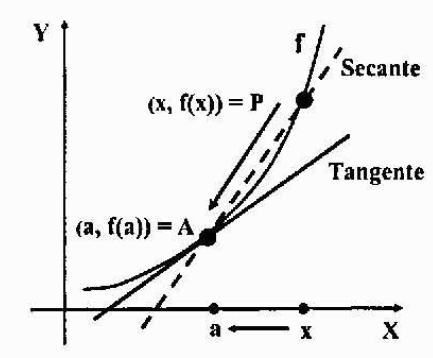
Aby uzyskać linię styczną, którą chcemy, konieczne jest obliczenie nachylenia, ponieważ mamy już punkt linii: punkt a.

Jeśli przeniesiemy punkt P przez wykres i coraz bardziej zbliżamy się do punktu A, wcześniej wspomniana sucha linia zbliży się do linii stycznej, którą chcesz znaleźć. Przyjmując limit, gdy „P zmierza do”, obie linie będą się pokrywać, dlatego ich stoki również.

Nachylenie linii segantów jest podane przez

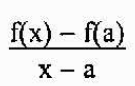
Stwierdzenie, że P jest bliski A, jest równoważne powiedzenie, że „X” zbliża się do „A”. Zatem nachylenie linii stycznej do wykresu F w punkcie A będzie równe:

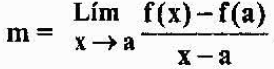
Poprzednie wyrażenie jest oznaczone przez F '(a) i jest definiowane jako pochodna funkcji f w punkcie „a”. Widzimy to analitycznie, pochodna funkcji w punkcie jest granicą, ale geometrycznie jest to nachylenie stycznej linii do wykresu funkcji w punkcie.

Może ci służyć: zmienna losowa: koncepcja, typy, przykłady

Teraz zobaczymy to pojęcie z punktu widzenia fizyki. Osiągniemy to samo wyrażenie poprzedniej granicy, chociaż inną ścieżką, uzyskując w ten sposób jednomyślność definicji.

Pochodna jako natychmiastowa prędkość poruszającego się obiektu

Spójrzmy na krótki przykład tego, co oznacza natychmiastowa prędkość. Kiedy powiedziano, na przykład, że samochód, który dotarł do miejsca docelowego, zrobił to z prędkością 100 km na godzinę, oznacza to, że za godzinę przejechał 100 km.

Niekoniecznie oznacza to, że przez całą godzinę samochód był zawsze 100 km, Vecimeter of the Car może w niektórych momentach oznaczać mniej lub więcej. Gdyby musiał stać na światłach, prędkość w tym momencie wynosiła 0 km. Jednak po godzinie trasa wynosiła 100 km.

Jest to znane jako średnia prędkość i jest podawana przez iloraz odległości przebywających między upływającym czasem, jak właśnie widzieliśmy. Tymczasem chwilowa prędkość jest tą, która w pewnej chwili (czas) wyznacza igłę Velocimetru samochodu (czas).

Zobaczmy to teraz bardziej ogólny sposób. Załóżmy, że obiekt porusza się wzdłuż linii i że to przemieszczenie jest reprezentowane za pomocą równania s = f (t), gdzie zmienna t mierzy czas i zmienną s przemieszczenie, biorąc pod uwagę jego początek w momencie t = 0, w którym to czasie jest również zero, to znaczy F (0) = 0.

Ta funkcja f (t) jest znana jako funkcja pozycji.

Wyrażenie chwilowej prędkości obiektu jest poszukiwane w ustalonej chwili. Przy tej prędkości oznaczamy to V (a).

Czy to w dowolnym momencie bliskim natychmiastowej „A”. W przedziale czasowym między „a” i „t” zmiana pozycji jest podana przez f (t) -f (a).

Średnia prędkość w tym przedziale czasowym wynosi:

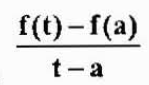
Który jest przybliżeniem szybkości chwilowej V (a). Takie podejście będzie lepsze, ponieważ zbliża się do „A”. Dlatego,

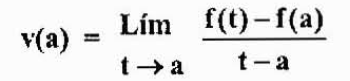
Zauważmy, że to wyrażenie jest równe w poprzednim przypadku, ale z innej perspektywy. Jest to znane jako pochodna funkcji f w punkcie „a” i jest oznaczona przez f '(a), jak stwierdzono powyżej.

Może ci służyć: prawa wykładników

Zauważ, że dokonanie zmiany H

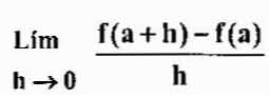
Oba wyrażenia są równoważne, ale czasami powinny być używane bardziej do jednego zamiast drugiego, w zależności od sprawy.

Następnie definiuje się bardziej ogólnie niż z funkcji F w dowolnym momencie „x” należącym do jej domeny jako

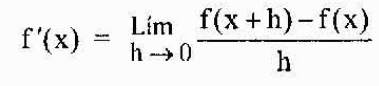
Najbardziej typową notacją reprezentującą pochodną funkcji y = f (x) jest ta, którą właśnie widzieliśmy (f 'o y'). Jednak kolejną szeroko stosowaną notacją jest notacja Leibniz, która jest reprezentowana jako którykolwiek z poniższych wyrażeń:

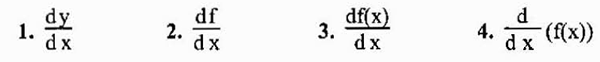
W związku z faktem, że pochodna jest w istocie granicą, może istnieć, ale nie zawsze istnieją granice. W przypadku, gdy istnieje, mówi się, że dana funkcja jest zróżnicowana w danym punkcie.

Funkcja algebraiczna

Funkcja algebraiczna jest połączeniem wielomianów poprzez sumy, odejmowanie, produkty, iloraz, moce i rodniki.

Wielomian jest wyrazem formy

P_N= a_NX^N+ Do_N-1X^N-1+ Do_N-2X^N-2+… + A₂X²+ Do₁x+a₀

Gdzie n jest naturalną liczbą i wszystkie_Siema, Z i = 0,1,… n to racjonalne liczby i_N≠ 0. W takim przypadku mówi się, że stopień tego wielomianu wynosi n.

Poniżej przedstawiono przykłady funkcji algebraicznych:

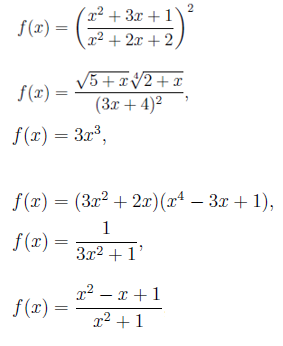
Tutaj funkcje wykładnicze, logarytmiczne i trygonometryczne nie są uwzględnione. Reguły wyprowadzania, które zobaczymy poniżej, są ogólnie ważne dla funkcji, ale ograniczymy je i zastosujemy w przypadku funkcji algebraicznych.

Zasady Derrying

Pochodzący ze stałego

Stwierdza, że ​​pochodna stałej wynosi zero. To znaczy, jeśli f (x) = c, to f '(x) = 0. Na przykład pochodna stałej funkcji 2 jest równa 0.

Pochodzący z mocy

Jeśli f (x) = x^N, Następnie f '(x) = nx^N-1. Na przykład X pochodna³ To jest 3x². W wyniku tego uzyskuje się, że wyprowadzona z funkcji tożsamości f (x) = x wynosi f '(x) = 1x^1-1= x⁰= 1.

Inny przykład jest następujący: Niech f (x) = 1/x², Następnie f (x) = x^-2 i f '(x) = -2x^-2-1= -2x^-3.

Ta właściwość jest również ważnymi korzeniami, ponieważ korzenie są racjonalnymi uprawnieniami, a powyższe można również zastosować w takim przypadku. Na przykład, pochodząca z korzenia kwadratowego jest podana przez

Może ci służyć: oszacowanie według interwałów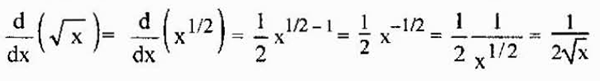

Pochodzący z suma i odejmowania

Jeśli f i g są funkcjami różnicowymi w x, wówczas suma f+g jest również i jest spełniona, że ​​(f+g) '(x) = f' (x)+g '(x) (x) (x).

Podobnie musisz (f -g) '(x) = f' (x) -G '(x). Innymi słowy, pochodna sumy (odejmowania) jest sumą (lub odejmowaniem) pochodnych.

Przykład

Jeśli h (x) = x²+X-1

H '(x) = (x²)+(x) '-(1)' = 2x+1-0 = 2x+1.

Produkt pochodzący z produktu

Jeśli f i g są funkcjami różnicowymi w x, wówczas produkt FG jest również różnicowany w x i jest to spełnione

(fg) '(x) = f' (x) g (x)+f (x) g '(x).

W konsekwencji ma, jeśli C jest stałą, a F jest funkcją różniczkową w x, wówczas CF jest również różnicząca w x y (cf) '(x) = cf' (x).

Przykład

Jeśli f (x) = 3x (x²+1), wtedy

f '(x) = (3x)' (x²+1)+(3x) (x²+1) '= 3 (x)' (x²+1)+3x [(x²) '+(1)]

= 3 (1) (x²+1)+3x [(2x^2-1) +0] = 3 (x²+1)+3x (2x) = 3x²+3+6x²

= 9x²+3.

Pochodzący z ilorazu

Jeśli f i g są różniczalne w x i g (x) ≠ 0, to f/g jest również różnicalne w x i jest to spełnione

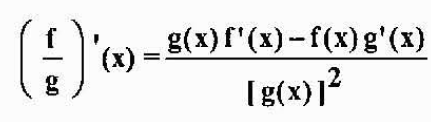
Przykład: Jeśli h (x) = x³/(X²-5x), zatem

H '(x) = [(x³) '(X⁵-5x)-(x³) (X⁵-5x) ']/ (x⁵-5x)²= [(3x²) (X⁵-5x)- (x³) (5x⁴-5)]/ (x⁵-5x)².

Zasada łańcuchowa

Ta reguła pozwala uzyskać skład funkcji. Ustanawia następujące czynności: jeśli y = f (u) jest różniczalny w u, a u = g (x) jest różniczalny w x, wówczas funkcja złożona f (g (x)) jest różniczna w x i jest to spełnione, że jest to spełnione [F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F G (X))] '= f' (g (x)) g '(x).

Oznacza to, że pochodna funkcji złożonej jest iloczynem pochodnej funkcji zewnętrznej (pochodnej zewnętrznej) przez uzyskaną funkcję wewnętrzną (pochodna wewnętrzna).

Przykład

Jeśli f (x) = (x⁴-2x)³, Więc

f '(x) = 3 (x⁴-2x)²(X⁴-2x) '= 3 (x⁴-2x)²(4x³-2).

Istnieją również wyniki obliczania przeciwwymiotnej pochodnej funkcji, a także uogólnienie na pochodne wyższego rzędu. Zastosowania są obszerne. Wśród nich wyróżniono ich zyski w optymalizacji i minimalnych funkcjach.

Bibliografia

1. Alarcon, s., González, m., & Quintana, H. (2008). Rachunek różny. Itm.
2. Cabrera, v. M. (1997). Obliczenia 4000. Progreso redakcyjne.
3. Castaño, godz. F. (2005). Matematyka przed obliczeniami. University of Medellin.
4. Eduardo, n. DO. (2003). Wprowadzenie do obliczeń. Umbral Editions.
5. Źródła, a. (2016). PODSTAWOWA MATEMATYKA. Wprowadzenie do obliczeń. Lulu.com.
6. Purcell, e. J., Rigdon, s. I., & Varberg, D. I. (2007). Obliczenie. Edukacja Pearsona.
7. Saenz, J. (2005). Rachunek różny (Drugi wyd.). Barquisimeto: hipotenusa.
8. Thomas, g. B., & Weir, m. D. (2006). Obliczenia: kilka zmiennych. Edukacja Pearsona.