Strona główna
Matematyka
Regularny, nieregularny decagon, właściwości, przykłady

Matematyka

Regularny, nieregularny decagon, właściwości, przykłady

On dekagon Jest to płaska postać z wielokątem w kształcie 10 stron i 10 wierzchołków lub końcówek. Dekagony mogą być regularne lub nieregularne, w pierwszym przypadku wszystkie strony i kąty wewnętrzne mają tę samą miarę, podczas gdy po drugiej stronie boki i/lub kąty są różne od siebie.

Rycina 1 pokazuje przykłady dekagonów każdego typu i jak widzimy, regularny decagon jest bardzo symetryczny.

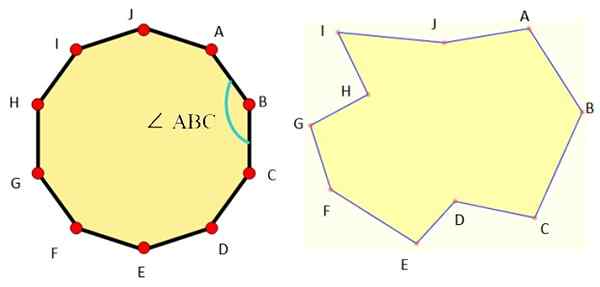Rysunek 1. Po lewej stronie regularny decagon i po prawej stronie nieregularny decagon. Źródło: Wikimedia Commons/F. Zapata/Mathpenref.

Podstawowe elementy wszystkich Decagon to:

-Boki, segmenty linii, które przy dołączeniu do decagonu.

-Wierzchołki lub punkty między każdą kolejną stroną.

-Kąty wewnętrzne i zewnętrzne między sąsiednimi stronami.

-Piagonals, segmenty, które łączą dwa nieobserwowe wierzchołki.

Wierzchołki są nazywane literami kapitałowymi, jak pokazano na rycinie 1, gdzie użyto pierwszych liter alfabetu, ale można użyć każdej litery.

Boki są symbolizowane dwiema literami wierzchołków, na przykład, strona AB jest ta między wierzchołkami a i b. W ten sam sposób, w jaki odbywa się to z przekątnymi, więc mamy przekątną AF, która dołącza do punktów A i F.

W przypadku kąty używamy tego symbolu: ∠, podobnie jak nachylony L. Na przykład kąt ∠ ABC to taki, którego wierzchołek to B i którego boki to segmenty AB i BC.

[TOC]

Zwykły decagon

W zwykłym dekagonie wszystkie strony mają tę samą miarę, a także kąty wewnętrzne. Dlatego mówi się, że tak jest równoboczny (równe strony) i równokątny (Równe kąty). Jest to bardzo symetryczna figura

Kąty wewnętrzne zwykłego decagonu

Aby znaleźć miarę wewnętrznych kątów zwykłego wielokąta, w tym zwykłego decagonu, stosuje się następującą formułę:

$I=\frac(n-2)\times 180^^on$

Gdzie:

-I jest miarą kąta w stopniach.

-n to liczba boków wielokąta. W przypadku decagon n = 10.

Może ci służyć: heptagon

Zastąpienie n = 10 w poprzednim wzorze Otrzymujemy następujące czynności:

$I=\frac(10-2)\times 180^^o10=144^^o$

Teraz mówi się, że jest wielokąt wypukły Jeśli jego miary kątowe są mniejsze niż 180º, w przeciwnym razie wielokąt jest wklęsły. Jak każdy wewnętrzny kąt regularnego decagonu mierzy 144º i jest mniejszy niż 180º, wówczas jest to wypukły wielokąt.

Suma kątów wewnętrznych

Suma miar wewnętrznych kątów dowolnego wielokąta wynosi w stopniach:

S = (n-2) x 180º; n jest zawsze większy niż 2

W tym formule musimy:

-S jest sumą miar kątów wewnętrznych.

-n to liczba stron. Dla decagon n = 10

Zastosowanie wzoru dla n = 10 wyników:

S = (10–2) x 180º = 1440º

Kąty zewnętrzne

Kąt zewnętrzny powstaje między jedną stroną a przedłużeniem sąsiedniej strony, zobaczmy:

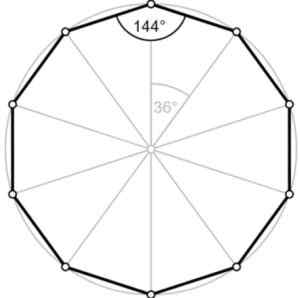
Rysunek 2.- Kąt zewnętrzny zwykłego decagonu mierzy 36º. Fontanna. Wikimedia Commons/F. Zapata.

Kąt ∠ ABC plus kąt zewnętrzny dodaje 180º, to znaczy są Uzupełniający. Dlatego kąt zewnętrzny jest równy 180º-144º = 36º, jak widzimy na rysunku.

Liczba przekątnych

Jak wspomniano wcześniej, przekątne są segmentami, które jednoczą wierzchołki nieobserwowe. Ile diagonalów możemy prześledzić w decegonie? Gdy liczba wierzchołków jest niewielka, można je łatwo zliczyć, ale gdy liczba ta wzrośnie, możesz stracić konto.

Na szczęście istnieje formuła, aby poznać liczbę przekątnych, które ma wielokąt N boki:

$D=\fracn(n-3)2$

Dla decagonu zastępujemy n = 10 i otrzymujemy:

D = 10 x (10–3) /2 = 35

W zwykłym dekagonie wszystkie przekątne są wycięte w jednym punkcie, co jest środkiem rysunku:

Rysunek 3. Kąty i przekątne zwykłego decagonu. Źródło: Wikimedia Commons.

Centrum

Środek wielokąta jest definiowany jako ten równoległe punkt dowolnego wierzchołka. Na poprzedniej figurze środek pokrywa się z punktem przecięcia wszystkich przekątnych.

Obwód

Jeśli zwykły decagon ma stronę A, jego obwód P jest sumą wszystkich stron:

Może ci służyć: 90 dzielników: co to jest i wyjaśnienie

P = 10.Do

Obszar

Znając długość Do Z boku zwykły obszar Decagon jest obliczany przez:

$A=\left (\frac52 \right )cot\left ( \frac\pi 10 \right )a^2$

Przybliżona formuła tego obszaru jest:

$A=\frac10a^24 \times tg\left ( \frac\pi 10 \right )\simeq 7.694a^2$

A trzecia opcja znalezienia obszaru jest długość apothem l_DO. To jest segment, który łączy się z punktu środkowego z jednej strony z środkiem wielokąta.

W takim przypadku obszar można obliczyć za pomocą wzoru:

$A=\fracP.L__A2=\frac10a\times L_A2$

Nieregularny decagon

Nieregularny decagon nie jest równoboczny ani równoznaczny, a ogólnie nie ma symetrii regularnej liczby, chociaż niektóre dekagony mogą mieć oś symetrii.

Mogą być również wypukłe lub wklęsłe, jeśli istnieją kąty wewnętrzne większe niż 180º.

Nieregularny decagon na rycinie 1 jest wklęsły, ponieważ niektóre z jego wewnętrznych kąty są większe niż 180º. Oczywiste jest, że istnieje wiele kombinacji kątów i stron, które powodują nieregularny decagon.

W każdym razie spełnia się, że:

-Wewnętrzne kąty nieregularnego decagonu również dodają 1440º.

-Ma również 35 przekątnych.

Obszar nieregularnego decagonu przez determinanty Gaussa

Zasadniczo nie ma unikalnej formuły do znalezienia obszaru nieregularnego wielokąta, ponieważ boki i kąty są różne. Możesz jednak znaleźć znajomość współrzędnych wierzchołków i obliczanie Determinanty Gaussa:

-Zadzwoń (x_N , I_N) do współrzędnych wierzchołków, z N od 1 do 10.

-Możesz zacząć od dowolnego wierzchołka, do którego zostaną przypisane współrzędne (x x₁, I₁). Teraz musisz zastąpić wartości każdej współrzędnej w tym wzorze:

$A=\left |\frac(x_1y_2-x_2y_1)+(x_2y_3-x_3y_2)+(x_3y_4-x_4y_3)+… (x_ny_1-x_1y_n)2 \right |$

Gdzie determinanty są dokładnie operacje między nawiasami.

-Ważne jest, aby pamiętać, że ostatni determinant obejmuje pierwszy wierzchołek wraz z ostatnim. Dla decagonu byłoby tak:

(X₁₀I₁ - X₁I₁₀)

Może ci służyć: interpolacja Lagrange

Ważny: Słupki mają wartość bezwzględną i oznaczają, że końcowy wynik jest zawsze z dodatnim znakiem.

Procedura może być pracochłonna, gdy liczba ma wiele wierzchołków, w przypadku decagonu odbywa się 10 operacji, więc wskazane jest stworzenie tabeli lub listy.

Ćwiczenie rozwiązane

Oblicz nieregularny obszar decagonowy pokazany na rysunku. Współrzędne wierzchołków to A, B, C ... J, których wartości są pokazane po lewej stronie.

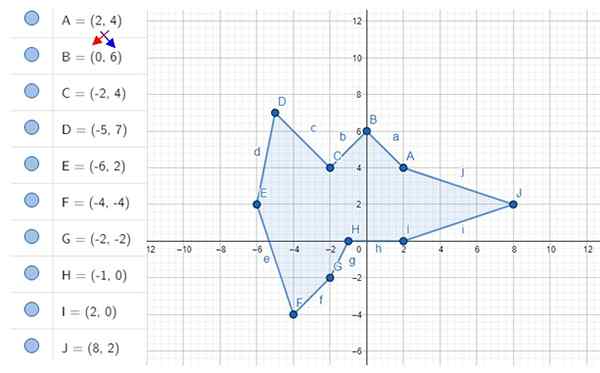Rysunek 4. Nieregularny decagon i jego wierzchołki. Źródło: f. Zapata z Geogebra.

Rozwiązanie

-Dokonujemy każdej z 10 operacji:

2 × 6 - 4 × 0 = 12 - 0 = 12
0 × 4 - 6 × (-2) = 0 + 12 = 12
(-2) × 7- 4 × (-5) = -14 + 20 = 6
(-5) × 2-7 × (-6) = -10 + 42 = 32
(-6) × (-4) -2 × (-4) = 24 + 8 = 32
(-4) × (-2)-(-4) × (-2) = 8-8 = 0
(-2) × 0-(-2) × (-1) = 0 -2
(-1) × 0 - 0 × (2) = 0 - 0 = 0
2 × 2 - 0 × 8 = 4 - 0 = 4
8 × 4-2 × 2 = 32 - 4 = 28

-Dodajemy wyniki:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Wynik dodatni jest uzyskiwany nawet bez prętów o wartości bezwzględnej, ale jeśli jest ujemny, to samo jest zmienione.

-Poprzedni wynik jest podzielony przez 2 i to jest obszar wielokąta:

A = 124/2 = 62

Właściwości Decangon

Poniżej znajduje się podsumowanie ogólnych właściwości decagonu, zarówno regularnego, jak i nieregularnego:

-Ma 10 stron i 10 wierzchołków.

-Suma kątów wewnętrznych wynosi 1440º.

-Istnieje 35 przekątnych.

-Obwód jest sumą wszystkich stron.

-Możesz tworzyć trójkąty w segmentach rysunku wielokąta od wierzchołka dla wszystkich innych. W dekagonie można w ten sposób narysować 8 trójkątów, jak pokazano poniżej:

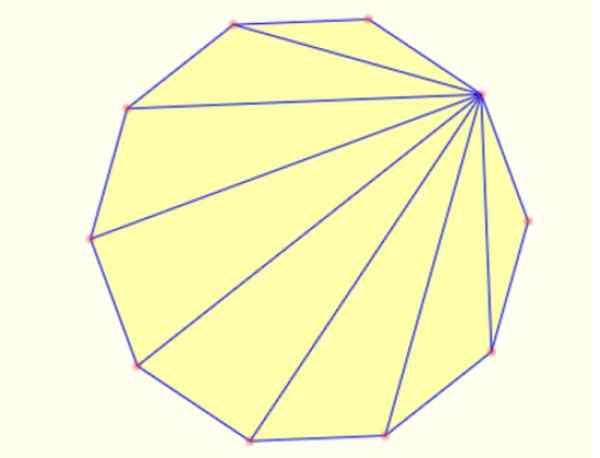Rysunek 5. Wewnętrzne trójkąty w zwykłym dekagonie. Źródło: Mathpenref.

Bibliografia

Alexander, zm. 2013. Geometria. 5. Wydanie. Cengage Learning.
Dekagon.com. Dekagon. Odzyskany z: decagon.com
Odniesienie do otwartego matematyki. Dekagon. Odzyskane z: Mathpenref.com.
Sangaku Maths. Elementy wielokąta i jego klasyfikacja. Odzyskany z: sangakoo.com.
Wikipedia. Dekagon. Odzyskane z: jest.Wikipedia.com.