Ile średnich ma obwód?

Obwód ma nieskończone średnice. Łatwo jest zauważyć, że tak jest, jeśli opiera się na definicji średnicy, która jest segmentem, który przechodzi jednocześnie przez środek obwodu i o dwa punkty tego samego.

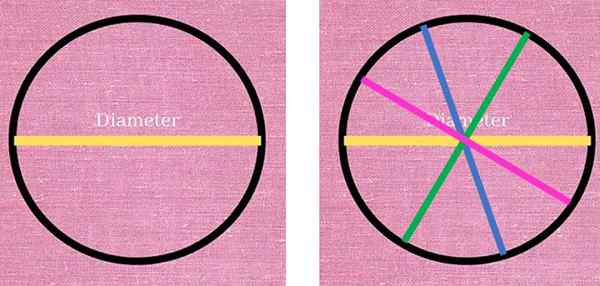
Na poniższym rysunku, po lewej stronie, żółta linia odpowiadająca średnicy obwodu jest obserwowana i podzielona na dwie części. Po prawej stronie narysowano trzy inne średnice w różnych kolorach: niebieski, zielony i różowy. Wszystkie mają taką samą długość i spełniają warunek łączenia dwóch punktów obwodu, przez środek tego samego.

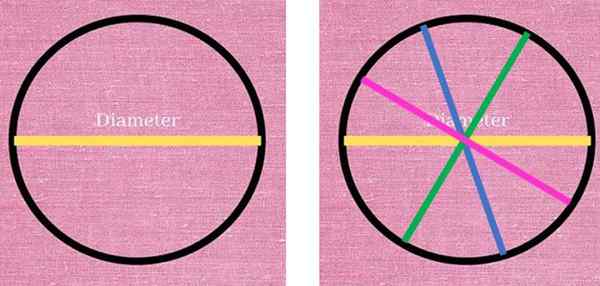Średnica jest charakterystycznym segmentem, który zawsze przechodzi przez środek obwodu i łączy dwa punkty tego. Po lewej stronie żółta średnica dzieli obwód na dwa. Po prawej stronie są inne średnice, które również dzielą obwód na dwie połówki. Źródło: f. Zapata.

Jak widać, możliwości rysowania średnic są nieograniczone, ponieważ nieskończone są punkty, które tworzą obwód. To samo można potwierdzić o promieniu, który jest segmentem, który łączy dowolny punkt obwodu z środkiem: można narysować nieskończoną liczbę radia.

A przy umieszczaniu od siebie dwóch przeciwnych radiotelefonów uzyskuje się średnicę, ponieważ promień mierzy połowę tego.

Średnica, długość radia i obwodu

Czy to średnica dowolnego obwodu i r, jego promień. Ponieważ średnica mierzy dwa razy więcej niż radio, można ją napisać:

D = 2 ∙ r

Oznacza to, że jeśli promień koła wynosi na przykład r = 5 cm, jego średnica wynosi d = 2 ∙ 5 cm = 10 cm.

Może ci służyć: Fibonacci Series: Właściwości, relacje naturalne, zastosowania

Średnica jest również znana jako Główna lina. Struny to linie lub segmenty, które są rysowane między dwoma punktami obwodu, ale niekoniecznie przechodzą przez centrum. Tylko średnica ma takie rozróżnienie.

Na poniższym rysunku widać różnicę i zobaczyć, dlaczego w efekcie średnica (czerwona) jest największym z ciągów, które można narysować na obwodzie:

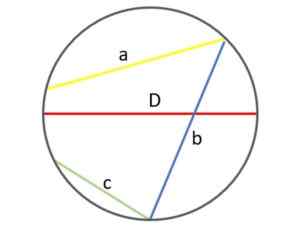Różne liny w obwodzie: średnica jest największa ze wszystkich. Źródło: f. Zapata.

Oczywiście miara średnicy (a zatem promień) jest taki sam w danym obwodzie. Według różnic, według mniejszego lub większego obwodu, zgodnie z.

Z drugiej strony, rozmiar ciągów tego samego obwodu jest różny, w zależności od tego, jak daleko lub w pobliżu punkty są punkty, które łączą się. W pokazanym przykładzie zielona lina „C” jest pozornie krótsza niż struny „A” i „B”.

A liczba ciągów, które można narysować, jest również nieskończona.

Obwód obwodu

Ze swojej strony długość obwodu jest równoważna jego obwodowi lub konturowi. Jest związany z jego średnicą, ponieważ im wyższy to obwód (jego obwód jest większy).

Stosunek lub iloraz między obwodem a średnicą jest stałą zwaną π (czyta „pi”). Wartość π wynosi 3.141592… punkty zawiesinowe wskazują, że ilość dziesiętnych i nieskończona, co jest powodem, ponieważ PI jest liczbą irracjonalną liczbą. Jednak w celach praktycznych PI może po prostu zaokrąglić 3.14

Może ci służyć: ile musisz dodać do 3/4, aby uzyskać 6/7?

Jeśli obwód jest oznaczony jako C i średnica jako D, powód ten jest podniesiony w następujący sposób:

C / d = π

Dlatego wzorem dla długości obwodu jest:

C = π ∙ d

Lub jeśli jest preferowany na podstawie promienia r:

C = 2π ∙ r

Obrazowy przykład

Obraz pokazuje trzy identyczne obwody, oznaczone literami A, B i C. W każdym z nich mrówek biegnie drogą na niebieskich segmentach kolorów, aby przejść od jednego punktu do drugiego obwodu.

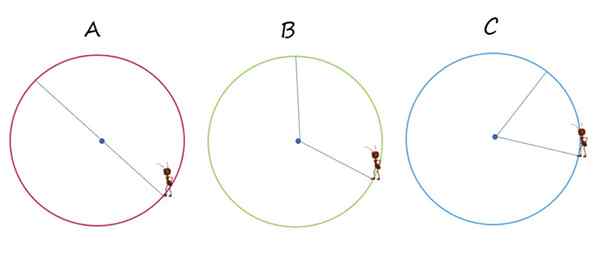Mrówka przesuwa się od jednego punktu do drugiego obwodu przez najcieńsze niebieskie linie. Źródło: f. Zapata.

1.- W którym przypadkach przemieszczenie występuje dokładnie na średnicy obwodu?

Odpowiedź

Tylko w przypadku a, ponieważ ta ścieżka przechodzi przez środek obwodu i przechodzi od jednego punktu do drugiego tego samego.

2.- Ile radia porusza się w każdym przypadku?

Odpowiedź

W każdym z trzech przypadków mrówka przemieszcza dwa radiotelefony obwodu.

3.- Która ze ścieżek odpowiada największej odległości?

Odpowiedź

Podróż jest równie długa w każdym przypadku, co odpowiada dwóm radiom obwodu.

4.- W takim przypadku mrówka jest dalej od punktu początkowego?

Odpowiedź

W przypadku A, ponieważ jest to właśnie przed nią, w pozostałych.

5.- I w takim przypadku mrówka kończy trasę bliżej punktu pochodzenia?

Może ci służyć: oznaki grupowania

Odpowiedź

W przypadku c.

6.- Jeśli promień obwodów wynosi 20 cm, ile centymetrów mierzy każdą trasę?

Odpowiedź

Ponieważ mrówek przenosi odległość równą dwóch radiotelefonów, całkowita przebyta odległość wynosi 40 cm.

Rozwiązane ćwiczenia

Ćwiczenie 1

Oblicz promień koła, którego średnica wynosi 4.5m.

Rozwiązanie

Radio ma połowę średnicy, jeśli mierzy to 4.5 cm, a następnie Radio R to 2.25 cm.

Ćwiczenie 2

Znajdź obwód obwodu ćwiczenia 1.

Rozwiązanie

Obwód jest obliczany przez średnicę lub przez promień, jak preferowane. W pierwszym przypadku:

C = π ∙ d

Zakładając, że π = 3.14 Do okrążenia wymiana wartości daje następujący wynik:

C = π ∙ d = 3.14 ∙ 4.5 cm = 14.13 cm

Ćwiczenie 3

Projektant jest proszony o narysowanie logo w kształcie serca, z wymiarami wskazanymi na rysunku. Zakrzywione części odpowiadają dokładnym półkole.

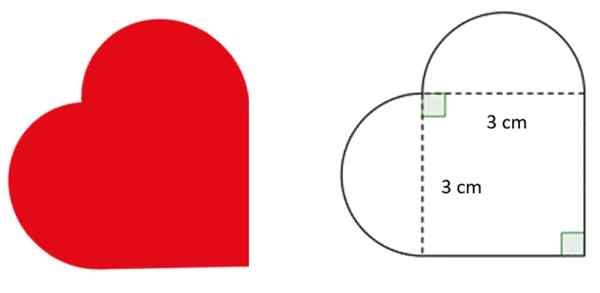
Z tymi informacjami odpowiedz:

1. Jaki jest promień półkolistów?
2. Ile kosztuje obwód serca?

Rozwiązanie

Średnica półokręgów jest równoważna z boku kwadratu, która wynosi 3 cm. Dlatego jego promień, który jest w połowie, mierzy 1.5 cm.

Rozwiązanie b

Obwód figury w kształcie serca jest sumą dwóch zewnętrznych stron kwadratu i obwodu półksiężyc. Podobnie jak identyczne, jego obwód jest równy pełnego okręgu o średnicy 3 cm:

C = π ∙ d = 3.14 ∙ 3 cm = 9.42 cm

Dlatego obwód P figury to:

P = 9.42 cm + 3 cm + 3 cm = 15.42 cm