Jakie są części płaszczyzny kartezjańskiej?

części płaszczyzny kartezjańskiej Składają się z dwóch prawdziwych, prostopadłych linii, które dzielą płaszczyznę kartezjańską na cztery regiony. Każdy z tych regionów nazywa się kwadrantami, a elementy płaszczyzny kartezjańskiej nazywane są punktami. Płaszczyzna wraz z osi współrzędnych jest wywoływana kartezjański samolot Na cześć francuskiego filozofa René Descartes, który wynalazł geometrię analityczną.

Dwie linie (lub osie współrzędnych) są prostopadłe, ponieważ tworzą kąt 90º między nimi i przekraczają wspólny punkt (pochodzenie). Jedna z linii jest pozioma, nazywa się pochodzeniem X (lub Abciisa), a druga linia jest pionowa, nazywa się pochodzeniem y (lub uporządkowanym).

Dodatnia połowa osi x jest po prawej stronie pochodzenia, a dodatnia połowa osi y jest początkiem. To pozwala na rozróżnienie czterech kwadrantów płaszczyzny kartezjańskiej, co jest bardzo przydatne podczas wykresu punktów w płaszczyźnie.

Punkty samolotu kartezjańskiego

W każdym punkcie P Samolotowi można przypisać kilka rzeczywistych liczb, które są jego współrzędnymi kartezjańskimi.

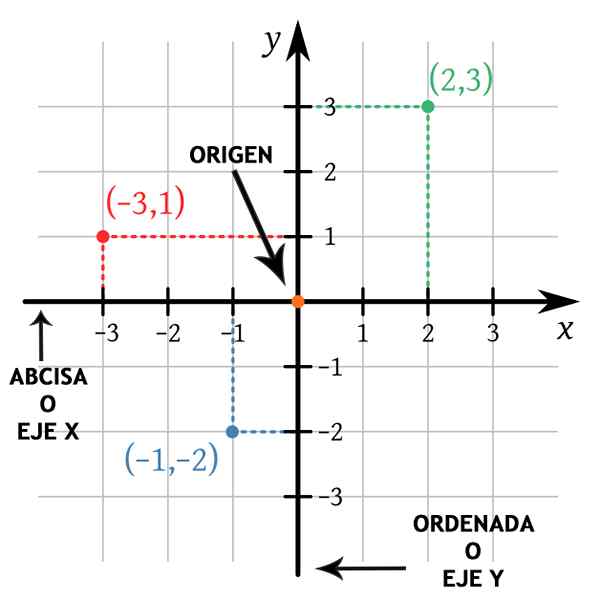
Jeśli przechodzą linia pozioma i linia pionowa P, I przecinasz się przy X i osi do osi y Do I B odpowiednio, wówczas współrzędne P Czy (Do,B). Jest to powołane (Do,B) Para uporządkowana i kolejność pisania liczb jest ważna.

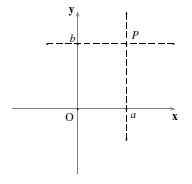
Pierwsza liczba, Do, Jest to współrzędna w „x” (lub odcięcie) i drugiej liczbie, B, Jest to współrzędna w „y” (lub uporządkowanym). Notacja jest używana P = (Do,B).

Jest oczywiste przez sposób, w jaki zbudowano płaszczyznę kartezjańską, że pochodzenie odpowiada osi „x” i 0 w osi „y”, to znaczy,, ALBO= (0,0).

Cuadies płaszczyzny kartezjańskiej

Jak widać na poprzednich liczbach, osie współrzędnych generują cztery różne regiony, które są kwadrantami płaszczyzny kartezjańskiej, które są oznaczone literami i, Ii, iii I Iv I różnią się od siebie w znaku, że punkty, które są w każdym z nich, mają.

Kwadrant Siema

Punkty kwadrantu Siema Są tymi, którzy mają oba współrzędne z pozytywnym znakiem, to znaczy ich współrzędna X i ich współrzędna i są pozytywne.

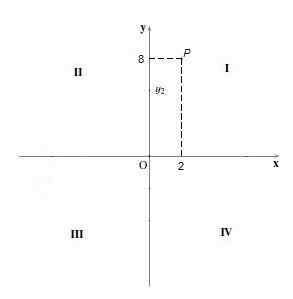
Na przykład punkt P = (2.8). Aby go wykazać, punkt 2 znajduje się na osi „x” i punkcie 8 na osi „y”, a następnie linie pionowe i poziome są rysowane odpowiednio, a tam, gdzie przecinają się, jest tam, gdzie jest punkt P.

Kwadrant Ii

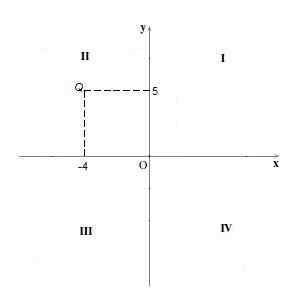
Punkty kwadrantu Ii Mają swoją negatywną współrzędną „X” i pozytywną współrzędną „Y”. Na przykład punkt Q = (-4,5). Jest to postępowanie graficzne, jak w poprzedniej sprawie.

Kwadrant Iii

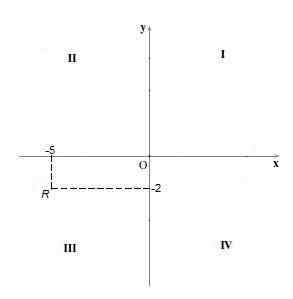
W tym kwadrancie znak obu współrzędnych jest ujemny, to znaczy współrzędna „x”, a współrzędna „y” są ujemne. Na przykład punkt r = (-5, -2).

Kwadrant Iv

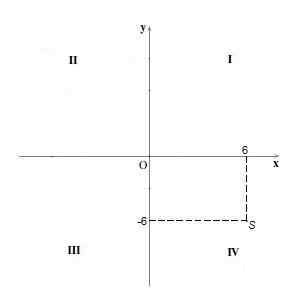
W kwadrancie Iv Punkty mają pozytywną i współrzędną współrzędną „y”. Na przykład punkt S = (6, -6).

Bibliografia

1. Fleming, w., & Varberg, D. (1991). Algebra i trygonometria z geometrią analityczną. Edukacja Pearsona.
2. Larson, r. (2010). Prealculus (8 wyd.). Cengage Learning.
3. Lojalny, j. M., & Viloria, n. G. (2005). Płaska geometria analityczna. Mérida - Wenezuela: Wenezuelan redakcja C. DO.
4. Oteyza, e. (2005). Geometria analityczna (Drugi wyd.). (G. T. Mendoza, wyd.) Edukacja Pearsona.
5. Oteyza, e. D., Osnaya, e. L., Garciadiego, c. H., Hoyo, a. M., & Flores, do. R. (2001). Geometria analityczna i trygonometria (Pierwszy wyd.). Edukacja Pearsona.
6. Purcell, e. J., Varberg, d., & Rigdon, s. I. (2007). Obliczenie (Dziewiąty ed.). Prentice Hall.
7. Scott, c. DO. (2009). Geometria płaszczyzny kartezjańskiej, część: analityczne stożki (1907) (Przedruk ed.). Źródło błyskawicy.