Sztywne ciało

Co to jest sztywne ciało?

Sztywne ciało to obiekt materialny, którego cząsteczki zawsze pozostają w tych samych pozycjach względnych. Dlatego jest to obiekt, który nie jest zdeformowany, jakość przypisana intensywnym siłom spójności, które utrzymują cząsteczki na miejscu.

W rzeczywistości cząsteczki dowolnego ciała podlegające sił zewnętrznych mają tendencję do wibracji lub poruszania się, więc obiekt jest zawsze deformowany do pewnego stopnia, ale efekty te są zwykle małe.

W takim przypadku można założyć, że ciało jest sztywne i ma bardzo dobre podejście do swojego zachowania, nawet jeśli jest to idealizacja.

Rodzaje ciał sztywnych

Możesz odróżnić dwa rodzaje sztywnego ciała:

• Ci, których cząsteczki są w dyskretnych ilościach, to znaczy mogą liczyć. Na przykład dwie metalowe kule połączone cienką i lekką prętą ​​można uznać za unikalny byt. Jeśli pręt jest wystarczająco sztywny, aby się nie zginać, system jest uważany za sztywny korpus.
• Te, które są ciągłe, co oznacza, że ​​cząstki, które je tworzą, są nie do odróżnienia. Codzienne i natury są dobrymi przykładami: kamienie, meble i inne, a także ziemia i inne niebiańskie skały skaliste.

Sztywny ruch ciała i dynamika

Podobnie jak obiekty uważane za cząstki, sztywne ciała można przenosić, obracać i mieć bardziej ogólny ruch, łącząc translację i obrót.

Aby zbadać tłumaczenie, nie jest to konieczne.

Te ruchy tłumaczenia i rotacji mogą być:

• Niezależny, jak w przypadku planet, które mają ruch obrotowy wokół ich osi (uważany za ustalony) i inny tłumaczenie wokół Słońca, ale prędkości każdego z nich nie są powiązane.
• Zepsuty kosz, jeśli powiązane są prędkość kątowa i prędkość tłumaczenia środka masy. W tym przypadku oś obrotu jest mobilna, jak w przypadku cylindra, który upada strzelanie bez poślizgnięcia się nachylonym nachyleniem.

Może ci służyć: pierwsze prawo termodynamiki: wzory, równania, przykłady

Dynamika sztywnego ciała stałego

Poniższe wielkości są istotne w dynamice sztywnej substancji stałej:

Mass Center

Środek masy jest punktem, w którym cała masa ciała jest uważana za skoncentrowaną. Jeśli jest to jednorodne i symetryczne ciało, jako kula, środek masy zbiega się z centrum geometrycznym.

Moment bezwładności

Ta skalarna wielkość jest wartością bezwładności obrotowej lub oporu, która sprzeciwia się obiektowi obracania się wokół pewnej osi. Zależy to całkowicie od geometrii obiektu i jego masy, a zatem w niektórych przypadkach łatwiej jest odwrócić pewne osie niż od innych.

W przypadku ciał o dobrze zdefiniowanych kształtach geometrycznych istnieją tabele z momentami bezwładności w odniesieniu do osi symetrii, na przykład ten, który przechodzi przez środek masy. Z tymi informacjami i twierdzeniami związanymi z momentem bezwładności, momenty w odniesieniu do innych osi można łatwo obliczyć.

Siły i moment obrotowy lub moment obrotowy

Siły są zobowiązane do poruszania ciała. Jeśli sztywne solidne centrum masy porusza się, równanie ruchu, zgodnie z drugim prawem Newtona, jest:

F_Internet = M ∙Do_cm

Gdzie:

-Siła netto jest F_Internet

-M to masa

-Przyspieszenie centrum masowego jest Do_cm

Jednak nie wszystkie siły stosowane przez obiek. Aby to zrobić, potrzebny jest moment obrotowy lub moment obrotowy, co mówi, jak skuteczne jest działanie obrotowe siły. Jest zdefiniowany jako produkt wektorowy między wektorem pozycji R Dotyczące pewnego punktu i siły F w pytaniu. Jest to oznaczone greckim listem τ (W odważnej liście jest to również wektor):

Może ci służyć: ruch eliptyczny

τ = R × F

W systemie międzynarodowym jednostką momentu obrotowego wynosi N⋅m (Newton na metr).

W wielu przypadkach ruch obrotowy wokół osi przechodzący przez środek masy jest opisany przez analogiczne równanie do drugiego prawa Newtona:

Gdzie indeks dolny „Z” odnosi się do osi obrotu, która przechodzi przez oś symetrii, ustaloną lub poruszającą się, ale bez zmiany kierunku, i_cm Jest to moment bezwładności w odniesieniu do centrum masy i α_z Jest to przyspieszenie kątowe ciała. Lato obejmuje wszystkie zewnętrzne momenty wokół osi Z.

Energia kinetyczna sztywnej substancji stałej

Ruch sztywnego ciała jest opisany przez tłumaczenia środka masy i obrotów wokół tego punktu, dlatego jego energia kinetyczna ma oba wkład.

Niech K energia kinetyczna ciała, v_cm Prędkość środka masy, m masa ciała i_cm jego moment bezwładności w odniesieniu do środka masy i ω prędkość kątowa. Można wykazać, że energia kinetyczna to:

K = ½ mV_cm² + ½ i_cm Ω²

Obserwuje się, że drugim terminem po prawej. Tam moment bezwładności odgrywa tę samą rolę co masa, podczas gdy prędkość kątowa odgrywa taką samą rolę jak prędkość liniowa.

Przykłady w życiu codziennym

Fizyczne wahadło

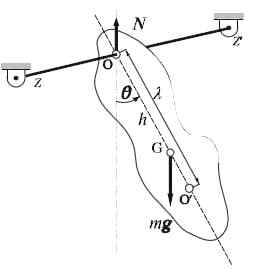Fizyczne wahadło

Fizyczne wahadło lub prawdziwe wahadło jest bardzo łatwe do zbudowania: składa się z sztywnej substancji stałej jak pręta lub pręt, swobodnie oscylującego wokół osi poziomej. Oś obrotu nie przekracza środka masy obiektu, co zasadniczo może mieć jakikolwiek kształt.

Może ci służyć: termometr oporności: charakterystyka, operacja, użycia

To wahadło różni się od prostego wahadła, ponieważ w tym ostatni.

Koło rowerowe

Koło rowerowe

Kolejnym znanym przykładem sztywnego korpusu jest koło rowerowe, którego oś przechodzi przez środek masy, który przecina środek koła. Tak długo, jak nie opierają się na boku lub obrotu, równania opisanej dynamiki mają zastosowanie do opisania twojego ruchu.

Kuchła do kręgli

Dobrym przykładem sztywnego ciała jest kulka do kręgli

Sztywny model stały bardzo dobrze dostosowuje się do opisania ruchu kulki do kręgli na torze lub gdy toczy się bez zsuwania się w dół rampy powrotnej.

Yoyo

Yoyo to popularna zabawka, którą można modelować jak sztywne ciało

Ta popularna zabawka jest wykonana z drewna lub plastikowego cylindra i liny przytłoczonej otaczającym miejscem.

Cylinder można modelować jako sztywny korpus, w którym napięcie w ciągu zapewnia moment obrotowy, podczas gdy waga (przyłożona do środka masy), a napięcie są odpowiedzialne za pionowe przyspieszenie środka masy.

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill. 
2. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
3.  Katz, d. 2013. Fizyka dla naukowców i inżynierów. Fundamenty i połączenia. Cengage Learning.
4. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1. osoba.
5. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wyd. Cengage Learning.