Elementy czworobokowe, właściwości, klasyfikacja, przykłady

A czworoboczny Jest to czterokątny wielokąt i cztery wierzchołki. Ich przeciwne strony Są tymi, którzy nie mają wspólnych wierzchołków, póki są kolejne strony Ci, którzy mają wspólny wierzchołek.

W czworoboku są sąsiednie kąty Ci, którzy dzielą stronę, a przeciwne kąty Nie mają wspólnych stron. Kolejną ważną cechą czworoboku jest to, że suma jego czterech Kąty wewnętrzne Jest dwa razy większy niż płaski kąt, czyli 360º lub 2π radian.

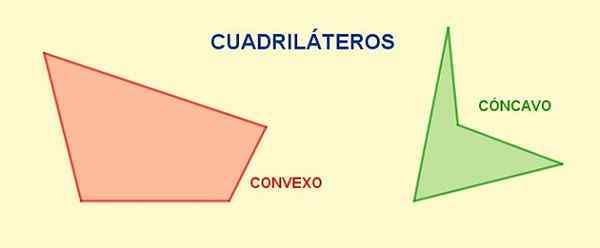
Rysunek 1. Różne czworobok. Źródło: f. Zapata.

Piagonals Są segmentami, które łączą wierzchołek z jego przeciwieństwem i na danym pierścieniu, z każdego wierzchołka. Całkowita liczba przekątnych czworoboku wynosi dwa.

Czworobok to postacie znane ludzkości od czasów starożytnych. Zapisy archeologiczne, a także konstrukcje, które przetrwają dzisiaj, potwierdzają.

Również dzisiaj czworobok nadal ma ważną obecność w codziennym życiu. Czytelnik może znaleźć ten formularz na ekranie, na którym tekst odczytuje w tym dokładnym momencie, w oknach, drzwiach, częściach samochodowych i niezliczonych miejscach.

[TOC]

Klasyfikacja czworoboku

Zgodnie z równoległością przeciwnych stron czworobokowe są klasyfikowane w następujący sposób:

1. Trapezoid, Gdy nie ma równoległości, a czworobok jest wypukły.
2. Trapez, Gdy między pojedynczą parą przeciwnych stron występuje równoległość.
3. Równoległobok, Kiedy ich przeciwne strony są równoległe od dwóch do dwóch.

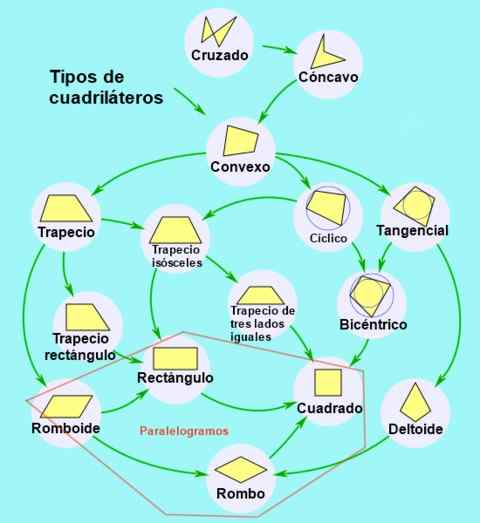Rysunek 2. Klasyfikacja i podklasyfikacja czworoboku. Źródło: Wikimedia Commons.

Rodzaje równoległoboku

Z kolei równoległoboki można klasyfikować zgodnie z ich kątami i stronami w następujący sposób:

1. Prostokąt, Jest to równoległobok, który ma cztery wewnętrzne kąty o równej miary. Wewnętrzne kąty prostokąta tworzą kąt prosty (90º).
2. Kwadrat, Jest to prostokąt z czterema stronami równej miary.
3. Diament, Jest to równoległobok z czterema stronami, ale jego różne sąsiednie kąty.
4. Romboid, równoległobok z różnymi sąsiednimi kątami.

Trapez

Trapez jest wypukłym czworobokiem z dwiema równoległymi stronami.

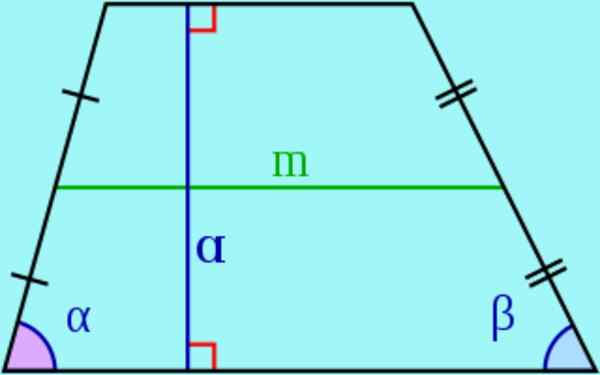Rysunek 3. Bazy, boczne, wysokość i mediana trapezu. Źródło: Wikimedia Commons.

- W trapezie nazywane są równoległe strony bazy I nazywane są paralle nie -paralle boczny.

- wysokość trapezu jest odległość między dwiema podstawami, to znaczy długość odcinka z końcami w podstawach i prostopadle do tego samego. Ten segment nazywany jest również wysokością trapezu.

- mediana To segment łączy punkty środkowe boków. Można wykazać, że mediana jest równoległa do podstaw trapezu, a jego długość jest równa półkomorom podstaw.

- Obszar trapezu to jego wysokość pomnożona przez półki podstawy:

Obszar trapezu = wysokość * (podstawa 1 + podstawa 2) / 2

Rodzaje trapezu

-Prostokąt trapezu: To ten, który ma stronę prostopadłą do podstaw. Ta strona jest również wysokością trapezu.

-Izosceli trapez: Ten z bokami równej długości. W trapezie Isosceles kąty przylegające do zasad są równe.

-Escaleno Trapezio: Ten, który ma swoje strony o różnej długości. Jego przeciwne kąty mogą być ostre, a drugie tępe, ale może się również zdarzyć, że oba są tępe lub oba ostre.

Może ci służyć: rozdzielone ćwiczenia czynnikowe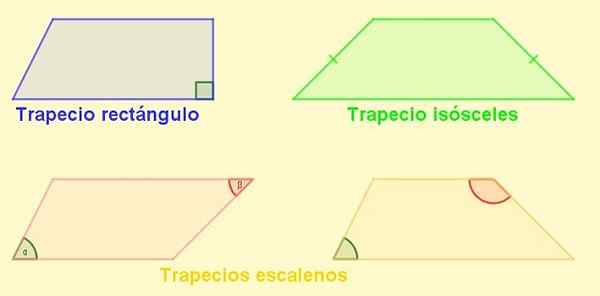 Rysunek 4. Rodzaje trapezu. Źródło: f. Zapata.

Równoległobok

Równoległobok jest czworobokiem, którego przeciwne strony są równoległe dwa do dwóch. W równoległoboku przeciwległe kąty są takie same, a sąsiednie kąty są uzupełniające, lub innymi słowy, sąsiednie kąty łącznie 180º.

Jeśli równoległobok ma kąt prosty, to wszystkie inne kąty będą również wywoływane prostokąt. Ale jeśli prostokąt ma również sąsiednie strony o tej samej długości, wszystkie jego boki są równe kwadrat.

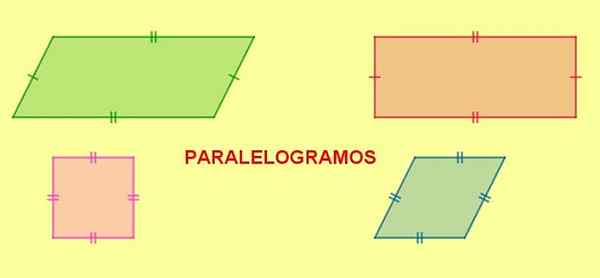Rysunek 5. Równoległoboki. Prostokąt, kwadrat i romb to równoległoboki. Źródło: f. Zapata.

Gdy równoległobok ma dwie sąsiednie strony o tej samej długości, wszystkie jego boki będą miały tę samą długość, a wynikową liczbą jest diament.

Wysokość równoległoboku jest segmentem z końcami po przeciwnych stronach i prostopadle do nich.

Obszar równoległoboku

Obszar równoległoboku jest iloczynem podstawy według jego wysokości, przy czym podstawa jest strona prostopadła do wysokości (ryc. 6).

Obszar równoległoboku = podstawa x wysokość = a . H

Przekątna równoległoboku

Kwadrat przekątnej, który zaczyna się od wierzchołka, jest równy sumę kwadratów dwóch stron przylegających do wspomnianego wierzchołka, bardziej podwójny produkt tych stron przez cosinus kąta tego wierzchołka:

F² = a² +  D² + 2 A D cos (α)

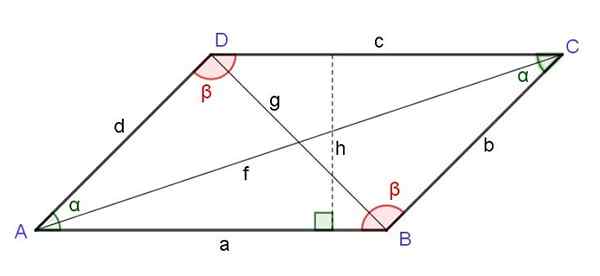Rysunek 6. Równoległobok. Przeciwne kąty, wysokość, przekątna. Źródło: f. Zapata.

Kwadrat przekątnej przeciwny wierzchołkowi równoległoboku jest równy sumę kwadratów dwóch boków przylegających do wspomnianego wierzchołka i odejmował podwójny produkt tych boków przez cosinus kąta tego wierzchołka:

G² = a² + D² - 2 A D cos (α)

Prawo równoległoboki

W każdym równoległobramie suma kwadratów ich boków jest równa sumie kwadratów przekątnych:

Do² + B² + C² + D² = f² + G²

Odnośniectangle

Prostokąt jest czworobokiem z przeciwnymi stronami równolegle od dwóch do dwóch, a także ma kąt prosty. To znaczy, że prostokąt jest rodzajem równoległoboku z kątem prostym. Do bycia równoległobramem, Prostokąt ma swoje przeciwne strony o równej długości a = c i b = d. 

Ale jak na każdym równoległobokowym kątach są uzupełniające, a równe przeciwległe kąty, w prostokącie poprzez kąt prosty, z konieczności tworzy proste kąty w pozostałych trzech kątach. To jest do powiedzenia W prostokącie wszystkie kąty wewnętrzne mierzą 90º lub π/2 Radian.

Przekątne prostokąta

W prostokącie przekątna są równa długość, Jak zostanie pokazane poniżej. Rozumowanie jest następujące; Prostokąt jest równoległobokiem ze wszystkimi jego prostymi kątami i dlatego dziedziczy wszystkie właściwości równoległoboku, w tym wzór, który daje długość przekątnej:

F² = a²+  D² + 2 A D cos (α)

G² = a² + D² - 2 A D cos (α)

z α = 90º

Jak Cos (90º) = 0, Zdarza się, że:

F² = g² = a² +  D²

To jest f = g, i dlatego długości F I G Z dwóch przekątnych prostokąta są równi, a ich długość jest podana przez:

Po przekątnej długości prostokąta = √ (a² + B²)

Ponadto, jeśli w prostokącie sąsiednich stron Do I B Jedna strona jest oparta na drugiej stronie, będzie wysokość, a zatem obszar prostokąta będzie:

Może ci służyć: Fibonacci Series: Właściwości, relacje naturalne, zastosowania

Obszar prostokąta = a x b.

Obwód jest sumą wszystkich stron prostokąta, ale ponieważ przeciwieństwa są takie same, jest to konieczne dla prostokąta boków Do I B Obwód jest podawany przez następujący wzór:

Obwód prostokąta = 2 (A + B)

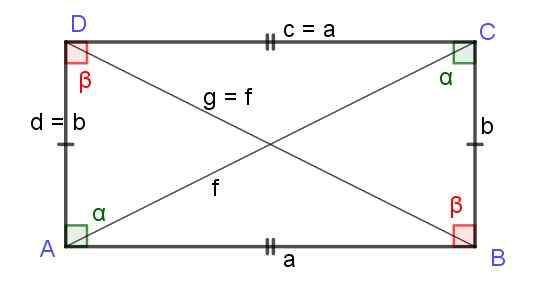Rysunek 7. Prostokąt boków a i b. Przekąski f i g mają równą długość. Źródło: f. Zapata.

Kwadrat

Kwadrat jest prostokątem z przylegającymi stronami o tej samej długości. Jeśli kwadrat ma stronę Do, Potem jego przekątne F I G Mają taką samą długość, jaka jest F = g = (√2) a.

Obszar kwadratu jest jego strona podwyższona do kwadratu:

Obszar kwadratu = a²

Obwód kwadratu jest dwa razy więcej:

Obwód kwadratu = 4 A

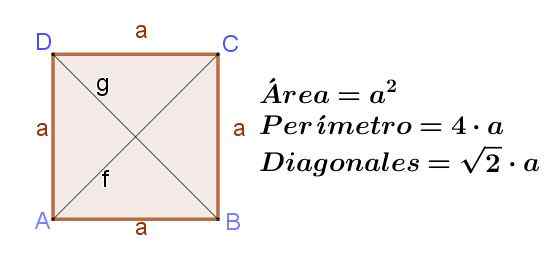Cyfra 8. Kwadrat na bok A, wskazujący jego obszar, obwód i długość przekątnych. Źródło: f. Zapata ..

Diament

Romb jest równoległobokiem z sąsiadującymi stronami o tej samej długości, ale jak na równoległoboku, przeciwne boki są takie same, Wszystkie strony romb są równa długość.

Przekątne romb są o różnej długości, ale są cięte pod kątem prostym.

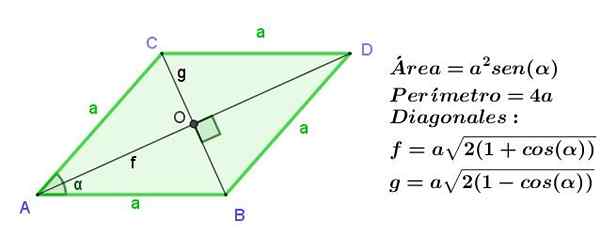Rysunek 9. Romb z boku A, wskazujący jego obszar, obwód i długość jego przekątnych. Źródło: f. Zapata.

Przykłady

Przykład 1

Wykazać, że w czworobocznym (nie skrzyżowanym) kątach wewnętrznych łącznie 360º.

Rycina 10: Wykazano to jako suma kąta czworobocznego Dodaj 360º. Źródło: f. Zapata.

ABCD jest uważany za ABCD (patrz ryc. 10) i rysowany jest przekątna BD. Powstają dwa trójkąty ABD i BCD. Suma wewnętrznych kątów trójkąta ABD wynosi:

α + β₁ + δ₁ = 180º

A suma wewnętrznych kątów trójkąta BCD to:

 β2 + γ + δ₂ = 180º

Dodanie dwóch równań jest uzyskiwane:

α + β₁ + δ₁ +  β₂ + γ + δ₂ = 180º + 180º

Grupowanie:

α + (β₁ +  β₂) + (δ₁ + δ₂) + γ = 2* 180º

Grupowanie i remont, w końcu wykazano, że:

α + β + δ + γ = 360º

Przykład 2

Wykazać, że mediana trapezu jest równoległa do jego podstaw, a jego długość jest półsizmem podstaw.

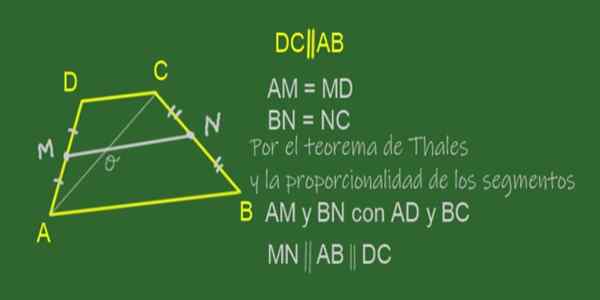Rysunek 11. Mediana Mn z trapezu ABCD. Źródło: f. Zapata.

Mediana trapezu jest segmentem, który łączy punkty środkowe jego boków, to znaczy niezrównoległe strony. W trapezie ABCD pokazanym na rycinie 11 mediana to Mn. 

Ponieważ jest to punkt środkowy AD i N Mid BC, spełnia się, że iloraz AM / AD i BN / BC są równe.

Oznacza to, że AM jest proporcjonalny do BN w tej samej proporcji co AD to BC, więc warunki zastosowania twierdzenia (wzajemnego) Thales, które potwierdzają następujące:

"Jeśli w trzech lub więcej prostych cięcie przez dwa segnt".

W naszym przypadku stwierdza się, że linie MN, AB i DC są równoległe do siebie, dlatego:

„LW medianie jednej z trapezu jest równolegle do jego podstaw".

Może ci służyć: połączone operacje

Teraz ma zastosowanie twierdzenie Thalesa:

"Zestaw podobieństw wyciętych przez dwa lub więcej suszenia określa proporcjonalne segmenty".

W naszym przypadku AD = 2 AM, AC = 2 AO, więc trójkąt DAC jest podobny do trójkąta MAO, a w konsekwencji DC = 2 miesiące.

Podobny argument pozwala potwierdzić, że Cu jest podobny do CON, gdzie Ca = 2 CO i CB = 2 CN. Wynika z tego, że AB = 2.

Krótko mówiąc, AB = 2 na y 2 miesiące. Więc kiedy wyszliśmy:

AB + DC = 2 ON + 2 M = 2 (MO + ON) = 2 mn

Wreszcie oczyszcza MN:

Mn = (AB + DC) /2

I stwierdza się, że mediana trapezu mierzy półki zasady lub innymi słowy: mediana mierzy sumę zasad, podzielona przez dwa.

Przykład 3

Pokazaj, że w rombce przekąski są przecięte pod kątem prostym.

Rysunek 12. Romb i demonstracja, że ​​ich przekątna są wycięte pod kątem prostym. Źródło: f. Zapata.

Tablica na rycinie 12 pokazuje niezbędną konstrukcję. Najpierw równoległobok ABCD jest rysowany z AB = BC, czyli romb. Przekątne AC i DB określają osiem kątów pokazanych na rysunku.

Za pomocą twierdzenia (a.Siema.P.) Stwierdza, że ​​wewnętrzne alternatywne kąty między podobieństwami przeciętymi przez siekant określają równe kąty, możemy ustalić, co następuje:

α₁ = γ₁, α2 = γ2, δ₁ = Β₁ i δ2 = β2. (*)

Z drugiej strony, ponieważ sąsiednie strony romb są o równej długości, określono cztery trójkąty izoscelesowe:

DAB, BCD, CDA i ABC

Teraz twierdzenie o trójkątach (izosceles) powołuje się na to, że kąty sąsiadujące z podstawą są równe miar, gdzie stwierdzono, że:

δ₁ = β2, δ2 = β₁, α2 = γ₁ i α₁ = γ2 (**)

Jeśli relacje (*) i (**) są łączone, osiągnięto kolejną równość kąta:

α₁ = α2 = γ₁ = γ₁ Z jednej strony i β₁ = Β2 = δ₁ = δ2 dla drugiego. 

Pamiętając o twierdzeniu równych trójkątów, które potwierdzają, że dwa trójkąty o równej stronie między dwoma równymi kątami są takie same:

Aod = aOB, a zatem także kąty ∡aod = ∡aOb.

Następnie ∡AOD + ∡AOB = 180º, ale ponieważ oba kąty mają równą miarę, 2 ∡AOD = 180º, co oznacza, że ​​∡aod = 90º.

Oznacza to, że geometrycznie wykazano, że przekątne romb są cięte pod kątem prostym.

Ćwiczenia rozwiązane

- Ćwiczenie 1

Wykazać, że w prostokątnym trapezie, kąty nie-EG są uzupełniające.

Rozwiązanie

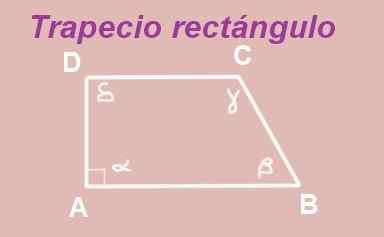Rysunek 13. Prostokąt trapezu. Źródło: f. Zapata.

Trapezoid ABCD jest zbudowany z równoległych baz AB i DC. Wewnętrzny kąt wierzchołka A jest prosty (mierzy 90º), więc masz prostokątny trapezoid.

Kąty α i δ są kątami wewnętrznymi między dwoma równoległymi paralelami AB i DC, dlatego są takie same, czyli δ = α = 90º. 

Z drugiej strony wykazano, że suma wewnętrznych kątów czworobocznego dodaje 360º, to znaczy:

α + β + γ + δ = 90º + β + 90º + δ = 360º.

Powyższe prowadzi do:

 β + δ = 180º

Potwierdzając to, co chciało zostać wykazane, że kąty β i δ są uzupełniające.

- Ćwiczenie 2

Równoległobok ABCD ma AB = 2 cm i AD = 1 cm, a ponadto kąt to 30º. Określ obszar wspomnianego równoległoboku i długość jego dwóch przekątnych.

Rozwiązanie

Obszar równoległoboku jest iloczynem długości jego podstawy według wysokości. W takim przypadku długość segmentu B = Ab = 2 cm zostanie przyjęta jako podstawa, druga strona ma długość a = ad = 1 cm, a wysokość h zostanie obliczona w następujący sposób:

H = ad * sin (30º) = 1 cm * (1/2) = ½ cm.

Następnie: obszar = b * h = 2 cm * ½ cm = 1 cm².

Bibliografia

1. C. I. DO. (2003). Elementy geometrii: z ćwiczeniami i geometrią kompasu. University of Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematyka 2. Grupa redakcyjna Patria.
3. Freed, k. (2007). Odkryj wielokąty. Benchmark Education Company.
4. Hendrik, v. (2013). Uogólnione wielokąty. Birkhäuser.
5. Iger. (S.F.). Matematyka pierwszy semestr Tacaná. Iger.
6. Jr. Geometria. (2014). Wielokąty. Lulu Press, Inc.
7. Miller, Heeren i Hornsby. (2006). Matematyka: rozumowanie i aplikacje (wydanie dziesiąta). Edukacja Pearsona.
8. Patiño, m. (2006). Matematyka 5. Progreso redakcyjne.
9. Wikipedia. Czworobok. Odzyskane z: jest.Wikipedia.com