Kryteria podobne trójkąty

Jakie są kryteria podobieństwa trójkątów?

Kryteria podobieństwa trójkątów to zasady, które pozwalają wiedzieć, czy dwa trójkąty są podobne. Podobieństwo liczb geometrycznych, w tym trójkąty, wymaga, aby liczby miały w ten sam sposób, chociaż niekoniecznie mają ten sam rozmiar lub taką samą orientację.

Aby dwa trójkąty były podobne, konieczne jest: i) ich homologiczne strony są proporcjonalne i ii) wewnętrzne kąty każdego z nich mają tę samą miarę.

Rysunek 1. Dwa podobne trójkąty: chociaż nie mają one tego samego rozmiaru, ich boki są proporcjonalne, a ich wewnętrzne kąty mają taką samą miarę. Źródło: f. Zapata.

Proporcjonalny stosunek lub proporcja między dwiema ilościami A i B jest reprezentowana przez stosunek A/B, z B ≠ 0. W przypadku podobnych trójkątów ważne są następujące proporcje między ich stronami:

a/a '= b/b' = c/c '= r

Wartość R jest nazywana Powód podobieństwa.

Ponadto odpowiednie kąty wewnętrzne muszą mieć tę samą miarę, zatem: ∠A = ∠A '; ∠B = ∠B 'i ∠C = ∠C'. Zgodnie z tymi warunkami kryteria podobieństwa trójkąty to:

Kryteria 1: Dwa trójkąty są podobne, jeśli mają dwa wewnętrzne kąty równej miary. Jeśli tak, trzeci kąt również mierzy to samo, ponieważ suma wewnętrznych kątów w dowolnym trójkącie wynosi 180º:

α = α '; β = β '

Kryteria 2: Trójkąty są podobne, jeśli dwie homologiczne strony są proporcjonalne, a kąt między nimi jest taki sam:

a/a '= b/b'; α = α '

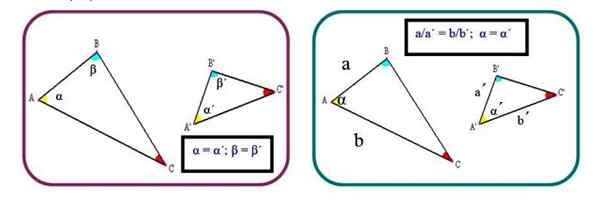Rysunek 2. Dwa kryteria ustalenia podobieństwa trójkątów. Źródło: f. Zapata.

Kryteria 3: Trzy homologiczne strony są proporcjonalne:

a/a '= b/b' = c/c '= r

Przykłady

Podobieństwo trójkątów jest bardzo przydatne do obliczania wysokości i odległości, które nie można bezpośrednio mierzyć bezpośrednio. Poprzez niektóre proste obliczenia można znaleźć te długości, porównując podobne trójkąty.

Może ci służyć: fundamentalne twierdzenie arytmetyki: demonstracja, zastosowania, ćwiczenia

Wysokość kolumn, budynków i drzew

Mówi się, że ojciec geometrii w starożytnej Grecji, taki jak Miletus (625-547 do.C.), obliczono wysokość kolumny świątyni bez potrzeby specjalnych instrumentów, po prostu porównywanie długości cienia jego trzciny z kolumną i zastosowanie podobieństwa trójkątów. Z tą samą metodą udało mu się zmierzyć wysokość wielkiej piramidy Egiptu, a tym samym zaimponować faraonowi.

Odległość do księżyca

Wykonany jest prosty eksperyment w celu obliczenia odległości między Ziemią a Księżycem. Wymaga waluty, odrobiny taśmy samoprzylepnej i nonszu lub reguły absolwenta. Kiedy księżyc jest pełny, waluta jest przymocowana do szklanki okna, a księżyc obserwuje się jednym okiem, położonym w taki sposób, że waluta obejmuje tylko księżyc w pełni.

Kiedy tak się dzieje, przyczyna między średnicą waluty a odległością między okiem a walutą jest taka sama, że ​​między średnicą księżyca a odległością między okiem a księżycem:

Średnica waluty/odległość Waluta = Średnica księżyca/odległość do księżyca

Przyczyną jest około 1/110. Co oznacza, że ​​odległość do księżyca wynosi 110 razy większa niż średnica tego.

Obecnie promień Księżyca szacuje się w 1737.1 km, więc jej średnica wynosi 3474.2 km. Zastępując tę ​​wartość w związku:

Odległość do księżyca = średnica księżyca ÷ (średnica waluty/odległość do waluty)

Otrzymuje:

Odległość do księżyca = 3474.2 km ÷ (1/110) = 382.162 km

Może ci służyć: pryzmat wątrobowy

Bardzo blisko wartości ustanowionej przez 384 astronomów.000 km.

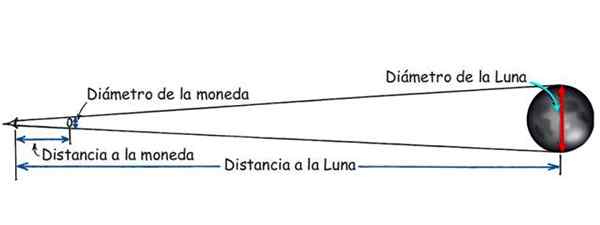Rysunek 3. Odległość do księżyca można znać dzięki podobieństwu trójkątów. Źródło: Zmodyfikowany Hewitt, str. Fizyka koncepcyjna.

Odległość między statkiem a brzegiem

Aby zmierzyć odległość między statkiem a brzegiem, stawki utknęły na plaży w punktach A, B, C i Q. Trójkąty ABC i PCQ są podobne według kryteriów 1, ponieważ mają dwa równe kąty: dwa kąty ∠C = α, które są przeciwne przez wierzchołek i dwa proste kąty równe 90º: ∠B = ∠Q.

Mówi się, że dwa trójkąty znajdują się w ten sposób Pozycja Thales I zawsze są podobne. Trójkąty są identyfikowane w pozycji Thales, aby mieć wspólny kąt, a przeciwne boki pod tym kątem są równoległe.

W następnej sekcji odbywa się ćwiczenie z wartościami numerycznymi.

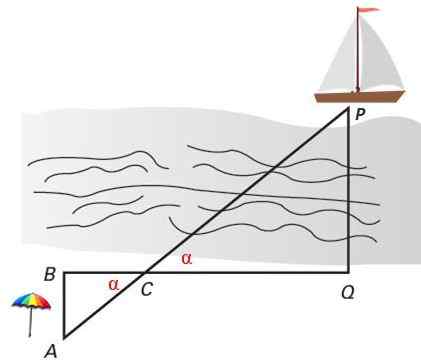Rysunek 4. Dwa podobne trójkąty w pozycji Thales służą do obliczenia prostopadłej odległości statku na brzeg. Źródło: f. Zapata.

Rozwiązane ćwiczenia

Ćwiczenie 1

Chcesz dowiedzieć się, jak daleko żaglówka jest zakotwiczona na poprzedniej figurze, z punktu, który znajduje się na brzegu plaży, dla którego stawki są przybite w punktach a, b, c i q, w ten sposób określając trójkąt ABC, który jest podobne do PCQ, ale których boki są łatwiejsze do pomiaru.

Oblicz prostopadłą odległość PQ między statkiem a brzegiem, podobieństwo trójkątów, jeśli dostępne są odległości:

AB = 12 m

BC = 16 m

QC = 60 m

Rozwiązanie

Proporcje między homologicznymi stronami to:

AB/QP = BC/CQ = 16 m/60 m = 0.267

Dlatego 0.267 jest przyczyną podobieństwa:

AB/QP = 0.267

QP = AB / 0.267 = 12 m / 0.267 = 44.9 m

Ćwiczenie 2

W poniższym trójkącie: ile mierzy segment reklam?

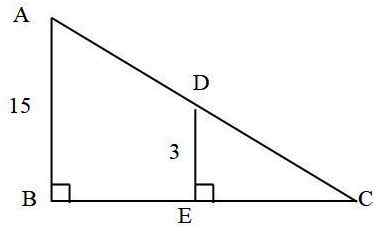
Wiadomo, że:

• AC = 25 cm
• AB = 15 cm
• De = 3 cm

Może ci służyć: wielokrotności 2: co to jest i wyjaśnienie

Rozwiązanie

Trójkąty są podobne, ponieważ mają kąt, który jest ∠C, a boki i AB są równoległe. Wskaźnik podobieństwa jest obliczany przez:

R = Ab / de = 15 cm / 3 cm = 5

A także przez:

R = AC / DC

Dlatego DC = AC / R = 25 cm / 5 = 5 cm

Od:

AC = AD + DC

Wynika z tego, że AD = AC - DC = 25 cm - 5 cm = 20 cm

Ćwiczenie 3

Trójkąt Isosceles ma obwód 49 cm i podstawę 21 cm. Oblicz obwód trójkąta podobnego do tego, ale którego podstawa mierzy 4 cm.

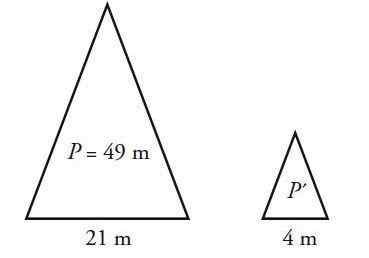
Rozwiązanie

Trójkąt Isosceles ma dwie równe strony, różni się od podstawy B. Niech ℓ miara boków i p obwód, który składa się z sumy trzech stron. Dla największego trójkąta:

P = 2 ℓ + B = 49 cm

2 ℓ + 21 cm = 49 cm → ℓ = (49-21) cm / 2 = 14 cm

Teraz odsetek między bokami trójkątów jest podniesiony, że z małego trójkąta są symbolizowane premiami:

B/ b '= ℓ/ ℓ'

21 cm / 4 cm = 14 cm / ℓ '→ → ℓ' = 14 cm / (21 cm / 4 cm) = 2.67 cm

Obwód małego trójkąta będzie:

P '= 2 ℓ' + b '= (2 x 2.67) cm + 4 cm = 9.33 cm.

Bibliografia

1. Alexander, zm. 2013. Geometria. 5. Wydanie. Cengage Learning.
2. Hewitt, Paul. 2012. Konceptualna nauka fizyczna. 5. Wyd. osoba.
3. Clemens, s. Geometria z aplikacjami. Addison Wesley.
4. Ibáñez, s. 1. 2010. Matematyka III. Cengage Learning.
5. Jiménez, r. Matematyka II: Geometria i trygonometria. 2. Wydanie. osoba.
6. Stewart, J. 2007. Przedłużanie. 5. Wydanie. Cengage Learning.
7. Vicmat. SAMOS Aristarco: Mierniki układu słonecznego. Odzyskany z: vicmat.com