Stała prędkości

Jaka jest stała prędkości?

stała prędkości Jest to stała proporcjonalności prawa prędkości kinetyki chemicznej, która ustanawia związek między stężeniem molowym odczynników a prędkością reakcji.

W miarę odczynników prędkości reakcji spożywają również zmniejszające się. Dlatego w obliczeniach stałej prędkości, reprezentowanej przez symbol „k”, początkowe prędkości są brane pod uwagę, aby mieć punkt porównawczy między kilkoma eksperymentami.

Kinetyka chemiczna wskazuje, że stała ta zależy od rzędów reakcji odczynników, których stężenia zmieniają prędkość reakcji.  Z drugiej strony, zgodnie z równaniem Arrheniusa, K zależy również od temperatury i energii aktywacji dla reakcji.

Dlatego mówi się, że stała prędkości nie jest prawdziwą stałą, ponieważ zmienia się w zależności od temperatury, a także w przypadku obecności katalizatorów, które modyfikują energię aktywacyjną. Dlatego nie ma wielu tabel, w których przychodzą one do określonych reakcji (i warunków).

Na przykład dla reakcji, w której reagują A i B, każdy z rzędem reakcji 1, stała zgłoszona k do 25 ° C, a przy dodaniu pewnej ilości katalizatora, nie będzie to samo, jeśli reakcja reakcja jest dokonywana do temperatury 26 lub 27 ° C. Najmniejsza zmienność wpłynie na wartość k, która jest tylko stała podczas warunków ustalonych dla eksperymentów.

Jak obliczyć stałą prędkości?

Eksperymentowanie

Określenie wartości stałej prędkości reakcji jest wykonywane eksperymentalnie. Jeśli na przykład chcesz określić wartość stałej prędkości dla reakcji formy:

A +B → C

W przypadku ustanowienia wartości k można dokonać trzech reakcji, z następującymi różnicami: W reakcji 2 początkowe stężenie odczynnika A jest stałe, [A], ale jest podwojone, na przykład stężenie odczynnika B, [[ B].

Tymczasem w reakcji 3 [a] jest podwojony w porównaniu z reakcją 1, utrzymując stałą [B].

Zatem zostanie zbudowana tabela stężeń, która będzie służyć do porównania początkowych prędkości między kilkoma eksperymentami. To w celu ustalenia zamówień reakcji i kolejnego obliczenia stałej prędkości.

Może ci służyć: wodorotlenek aluminiowy: struktura, właściwości, zastosowania, ryzyko

Zamówienia reakcji

Pierwsze obliczenia

Dla poprzedniej reakcji jego prędkość wyraża równanie:

Prędkość reakcji = K · [a]^X· [B]^I

Gdzie „x 'e” i' odpowiadają odpowiednio zleceniom reakcji odczynników A i B.

Aby określić wartości rzędów reakcji, należy dokonać porównania między reakcją 2 i 1, a także między reakcją 3 i 1.

Porównując reakcję 1 z 2, można było na przykład zaobserwować, że poprzez powielanie [B] istnieje powielanie prędkości reakcji.

Następnie: odsetek [B] między reakcjami 2 i 1 wynosi 2, a także proporcja między prędkościami reakcji. Następnie można uzyskać wartość rzędu reakcji w odniesieniu do B (wykładnik i), poprzez następujące podejście:

Obliczanie kolejności reakcji „i”. Źródło: Gabriel Bolívar.

Prędkość eksperymentu 2 jest dwa razy szybsza niż prędkość eksperymentu 1. W ten sposób podzielenie dwóch powyższych równań będziemy mieli:

2 = 2^I

Dlatego „i„ vale 1, możliwość stwierdzenia, że ​​porządek reakcji w odniesieniu do odczynnika B jest pierwszego rzędu.

Drugie obliczenia

W ten sam sposób kontynuujemy odczynnik A do obliczenia „x”:

Obliczanie rzędu reakcji „x”. Źródło: Gabriel Bolívar.

Szybkość eksperymentu lub reakcji 3 jest czterokrotnie wyższa niż eksperyment lub reakcja 1. Dlatego:

4 = 2^X

ALBO

2² = 2^X

A wartość x wynosi 2, więc reakcja jest drugim rzędem w stosunku do odczynnika do.

Ostateczne rozliczenie

Następnie można ustalić wartość stałej prędkości w oparciu o którąkolwiek z reakcji:

Prędkość reakcji = K · [a]²· [B]

Wystarczająco, aby wprowadzić wartości eksperymentalne i wyczyścić K:

K = prędkość reakcji / ([a]²· [B])

Przykłady

Poniższe przykłady służą jako wprowadzenie, zanim ćwiczenia zostały rozwiązane z następnego rozdziału.

Przykład 1

W reakcji chemicznej:

a) Jeśli początkowe stężenie odczynnika jest podwojone prędkość reakcji: jaki jest rzędu reakcji w odniesieniu do tego odczynnika?

b) Jeżeli wzrost stężenia odczynnika powoduje wzrost prędkości w współczynniku 8, jaki byłby kolejność reakcji?

c) Jeżeli stężenie odczynnika doświadczy zmiany, a prędkość pozostaje taka sama: jaki jest rzędu reakcji w odniesieniu do odczynnika?

Może ci służyć: cykopropan (C3H6)

W a) odsetek prędkości reakcji jest taki sam, a odsetek stężeń odczynników jest równy 2^X,

2 = 2^X

Dlatego x = 1, a kolejność reakcji w odniesieniu do odczynnika wynosi 1.

W b) odsetek prędkości reakcji jest taki sam 8 (2³), a odsetek stężeń odczynników jest równy 2^X,

2³ = 2^X

Dlatego x = 3, a kolejność reakcji w odniesieniu do odczynnika wynosi 3-

Podczas gdy w c) prędkość reakcji jest niezależna od stężenia odczynnika, więc rzędu reakcji w odniesieniu do odczynnika wynosi zero.

Przykład 2

Reakcja:

2 nie₂  +  ALBO₂ → 2 nie₂

Ma wyrażenie następującego prawa prędkości:

Prędkość reakcji = k · [nie₂]²·ALBO₂.

Jaki jest globalny porządek reakcji? Jakie jednostki miałyby K?

Kolejność reakcji dotyczącej lub₂ Jest to 1, a kolejność reakcji w odniesieniu do nie₂ Jest to 2, więc globalny porządek reakcji jest sumą tych wartości, to znaczy 2 + 1 = 3.

Szybkość reakcji ma jednostki M/S, a stężenia odczynników wyrażono w M. Przeprowadzając analizę jednostek, które będziemy mieli:

k = prędkość reakcji / ([nie₂]²·[ALBO₂]

= (M / s) / (m³)

= s^-1M^-2

Rozwiązane ćwiczenia

Ćwiczenie 1

Dane z następującej reakcji uzyskano w 25 ° C:

A +2 B → C +2 D

Jaki jest wyrażenie prawa prędkości tej reakcji? Jaka jest wartość stałej prędkości?

Obliczenia zamówień reakcji

Dane eksperymentalne to:

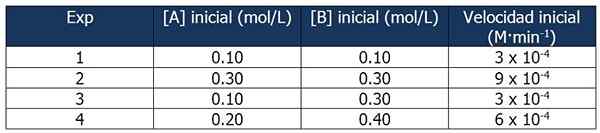Dane kinowe z ćwiczenia 1. Źródło: Gabriel Bolívar.

Porównanie eksperymentów 1 i 3 pozwala wyciągnąć następujące wnioski:

Proporcja między prędkościami reakcji 3 i 1:

3 x 10^-4 M · min^-1 / 3 x 10^-4 M · min^-1 = 1

Ale proporcja między stężeniami B wynosi:

(0.3 mol / l) / (0.1 mol/l) = 3

Szybkość reakcji jest niezależna od stężenia B, ponieważ jej wzrost nie wpływa. Dlatego kolejność reakcji w odniesieniu do odczynnika B wynosi zero.

Z drugiej strony porównanie reakcji 4 i 1 pozwala na następujące wnioski:

6 x 10^-4 M · min^-1 / 3 x 10^-4 M · min^-1 = 2

Tymczasem proporcja między [a] reakcji 4 i 1 jest równa:

Może ci służyć: 5 cech jednorodnych mieszanin

(0.20 mol / l) / (0.10 mol/l) = 2^X

Wówczas związek między proporcjami będzie:

2 = 2^X

x = 1

Dlatego wyrażenie prawa prędkości jest:

Prędkość reakcji = K · [a]

B nie jest przyjmowane, ponieważ jego kolejność reakcji wynosi zero.

Obliczanie k

Możemy obliczyć stałą prędkości na podstawie dowolnego danych kinetycznych. Użyjmy eksperymentu 1:

K = prędkość reakcji / [a]

= 3 x 10^-4 M · min^-1 / 0.10 m

= 3 x 10^-3 lub 0.003 min^-1

Ćwiczenie 2

Dane dotyczące prędkości reakcji uzyskano w określonej temperaturze.

2 Clo₂ (AC) +2 OH^- (AC) → CLO₃^- (AC) +CLO₂ (AC) +H₂Lub (l)

Obliczenia zamówień reakcji

Dane eksperymentalne to:

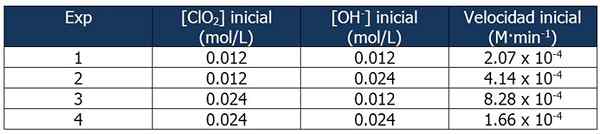Dane kinowe dotyczące ćwiczeń 2. Źródło: Gabriel Bolívar.

Proporcja między prędkościami reakcji 2 a reakcją 1 wynosi:

4.14 x 10^-4 M · min^-1 / 2.07 x 10^-4 M · min^-1 = 2

I odsetek stężeń OH^- Między reakcjami 2 i 1 jest równe:

(0,024 mol/l)/(0,012 mol/l) = 2^X

Wykładnik „x” reprezentuje kolejność reakcji w odniesieniu do odczynnika OH^-. Zależność między obliczonymi proporcjami można przedstawić w następujący sposób:

2 = 2^X

x = 1

Dlatego kolejność reakcji w odniesieniu do odczynnika OH^- jest równe 1.

W reakcji 3 stężenie CLO jest podwojone₂ reakcji 1, podczas gdy stężenie OH^- Pozostaje stała.

Proporcja między prędkościami reakcji 3 i 1:

(8.28 x 10^-4 M · min^-1) / (2.07 x 10^-4 M · min^-1) = 4 (2²)

I odsetek [Clo₂] między reakcjami 3 i 1 jest równe:

(0,024 mol/l)/(0,012 mol/l) = 2^I

Wykładnik „i” reprezentuje kolejność reakcji dotyczącej odczynnika CLO₂.

Porównanie proporcji:

2² = 2^I

4 = 2^I

y = 2

Dlatego reakcja jest druga w odniesieniu do odczynnika CLO₂.

Wyrażenie prawa prędkości będzie wtedy:

Prędkość reakcji = k · [CLO₂]²· [Oh^-]

Obliczanie k

Ponownie możemy obliczyć k na podstawie poprzedniego wyrażenia przy użyciu dowolnego z danych kinetycznych dla eksperymentów. Użyjemy eksperymentu 3:

K = (8.28 x 10^-4 M · min^-1) / (0.024 m)² (0.012 m)

= 119.79 min^-1· M^-2

Bibliografia

1. Whitten, Davis, Peck i Stanley. (2008). Chemia. (8 wyd.). Cengage Learning.
2. Wikipedia. (2020). Stała szybkości reakcji. Źródło: w:.Wikipedia.org
3. Chemistry Texas A&M University. (S.F.). Kinetyka: obliczenia stawki próbkowania. Odzyskane z: chem.Tamu.Edu
4. Keith J. Laidler. (2020). Szybkość reakcji. Britannica Encyclopaedia. Odzyskane z: Britannica.com
5. Helmestine, Anne Marie, pH.D. (25 sierpnia 2020). Jaka jest stała prędkości w chemii? Odzyskane z: Thoughtco.com
6. Clark Jim. (2013). Stałe i równanie Arrheniusa. Odzyskane z: chemguide.współ.Wielka Brytania