Stała proporcjonalności Czym jest, obliczanie, ćwiczenia

stała proporcjonalności Jest to relacyjny element numeryczny, używany do zdefiniowania wzorca podobieństwa między 2 wielkościami, które są jednocześnie zmieniane. Bardzo często reprezentuje go jako ogólną funkcję liniową poprzez wyrażenie f (x) = k.X. Nie jest to jednak jedyna reprezentacja możliwej proporcjonalności.

Na przykład związek między x i y w funkcji y = 3x ma stałą proporcjonalności równej 3. Pokazuje, że gdy zmienna niezależna X rośnie, podobnie jak zmienna zależna i w potrójnej jej poprzedniej wartości.

Zmiany stosowane w jednej zmiennej mają natychmiastowe reperkusje, tak że istnieje wartość znana jako stała proporcjonalności. Służy to do powiązania różnych wielkości, które nabywają obie zmienne.

[TOC]

Jaka jest stała proporcjonalności i typów

Zgodnie z trendem zmiany zmiennych proporcjonalność można podzielić na 2 typy.

Bezpośrednia proporcjonalność

Sugeruje jednokierunkowy związek między dwoma wielkościami. W nim, jeśli zmienna niezależna stanowi pewien wzrost, zmienna zależna również wzrośnie. Podobnie wszelkie zmniejszenie zmiennej niezależnej spowoduje spadek wielkości i.

Na przykład funkcja liniowa zastosowana we wstępie; Y = 3x, odpowiada bezpośrednio proporcjonalności. Wynika to z faktu, że wzrost zmiennej niezależnej x spowoduje wzrost potrójnej w poprzedniej wartości przyjętych przez zmienną zależną i.

Podobnie zmienna zależna zmniejszy swoją wartość potrójną, gdy X opada wielkość.

Wartość stałej proporcjonalności „K” w bezpośrednim związku jest zdefiniowana jako k = y/x.

Odwrotna lub pośrednia proporcjonalność

W tego typu funkcjach związek między zmiennymi jest przedstawiany w sposób antonimiczny, w którym wzrost lub spadek zmiennej niezależnej odpowiada odpowiednio spadku lub wzrostowi zmiennej zależnej.

Może ci służyć: rozkład liczb naturalnych (przykłady i ćwiczenia)

Na przykład funkcja f (x) = k/x jest relacją odwrotną lub pośrednią. Ponieważ wartość zmiennej niezależnej zaczyna rosnąć, wartość k zostanie podzielona przez liczbę rosnącą, co spowoduje zmniejszenie wartości zależnej według proporcji.

Zgodnie z wartością przyjętą przez k, tendencję proporcjonalnej funkcji odwrotnej można zdefiniować. Jeśli k> 0, funkcja będzie zmniejszała się we wszystkich liczbach rzeczywistych. A jego wykres będzie zlokalizowany w 1. i 3. kwadrancie.

Przeciwnie, jeśli wartość k jest ujemna lub mniejsza niż zero, funkcja będzie rosła, a jej wykres zostanie znaleziony w 2. i 4 kwadrancie.

Jak to jest obliczane?

Istnieją różne konteksty, w których może być wymagana definicja stałej proporcjonalności. W różnych przypadkach zostaną pokazane różne dane dotyczące problemu, gdzie ich badanie w końcu pokaże wartość k.

W ogólny sposób wspomniane można podsumować. Wartości K odpowiadają dwóm wyrażeniom według rodzaju obecnej proporcjonalności:

- Direct: k = y/x

- Odwrotne lub pośrednie: k = y.X

Według twojego wykresu

Czasami tylko wykres funkcji będzie znany częściowo lub całkowicie. W takich przypadkach będzie to konieczne, według analizy graficznej, określić rodzaj proporcjonalności. Następnie będziemy musieli zdefiniować współrzędną, która pozwala zweryfikować wartości x i y w celu zastosowania do odpowiedniej formuły k.

Wykresy odnoszące się do bezpośredniej proporcjonalności są typu liniowego. Z drugiej strony wykresy odwrotnych funkcji proporcjonalnych zwykle nabierają kształtu hiperboli.

Zgodnie z tabelą wartości

W niektórych przypadkach istnieje tabela wartości z wartościami odpowiadającymi każdej iteracji zmiennej niezależnej. Zwykle implikuje to realizację wykresu oprócz zdefiniowania wartości k.

Może ci służyć: Rozkład częstotliwości: jak zrobić tabelę, przykład, ćwiczenie

Zgodnie z wyrażeniem analitycznym

Pokazuje wyrażenie, które określa analitycznie. Bezpośrednio wartość k może być jasna lub może być również wywnioskowana z samego wyrażenia.

Z reguły trzech bezpośrednich lub złożonych

W innych modelach ćwiczeń znajdują się pewne dane, które odnoszą się do związku między wartościami. To sprawia, że ​​konieczne zastosowanie trzech bezpośrednich lub złożonych w celu zdefiniowania innych niezbędnych danych w ciągu roku.

Historia

Koncepcja proporcjonalności zawsze była obecna. Nie tylko w umyśle i pracy wielkich matematyków, ale w codziennym życiu populacji, ze względu na ich praktyczność i możliwość zastosowania.

Bardzo często spotyka się sytuacje wymagające proporcjonalności. Są one przedstawione w każdym przypadku, w którym porównywane są zmienne i zjawiska, które utrzymują pewne relacje.

Dzięki osi czasu możemy scharakteryzować momenty historyczne, w których zastosowano postępy matematyczne dotyczące proporcjonalności.

- Drugi wiek a.C. Przyjęto system przechowywania frakcji i proporcji w Grecji.

- Piąty wiek a.C. Proporcja, która odnosi stronę i przekątna kwadratu, jest również odkryta w Grecji.

- 600 a.C. Tales de Mileto przedstawia swoje twierdzenie dotyczące proporcjonalności.

- Rok 900. System dziesiętny wcześniej stosowany przez Indie z powodów i proporcji jest rozszerzony. Wkład wniesiony przez Arabów.

- XVII Century. Wkłady odnoszą się do proporcji w obliczeniach przybycia Eulera.

- XIX wiek. Gauss zapewnia koncepcję liczby złożonej i proporcji.

- Dwudziesty wiek. Proporcjonalność jako model funkcyjny jest definiowany przez cukier i deulofeo.

Rozwiązane ćwiczenia

Ćwiczenie 1

Wymagane jest obliczenie wartości zmiennych x, y, z i g. Znajomość następujących relacji proporcjonalnych:

3x + 2y - 6z + 8g = 1925

Może ci służyć: ciągła losowa zmienna

x/3 = y/8 = z/3 = g/5

Zdefiniowano względne wartości stałej proporcjonalności. Można je uzyskać z drugiej relacji, w której wartość dzielona każdej zmiennej wskazuje związek lub powód dotyczący k.

X = 3k y = 2k z = 3k g = 5k

Wartości są zastąpione w pierwszym wyrażeniu, w którym nowy system zostanie oceniony w jednej zmiennej K.

3 (3k) + 2 (2k) - 6 (3k) + 8 (5k) = 1925

9K + 4K -18k + 40k = 1925

35K = 1925

K = 1925/35 = 55

Korzystając z tej wartości stałej proporcjonalności, możemy znaleźć figurę, która określa każdą ze zmiennych.

x = 3 (55) = 165 y = 2 (55) = 110

Z = 3 (55) = 165 g = 5 (55) = 275

Ćwiczenie 2

Obliczyć stałą proporcjonalności i wyrażenie, które definiuje funkcję, biorąc pod uwagę jej grafikę.

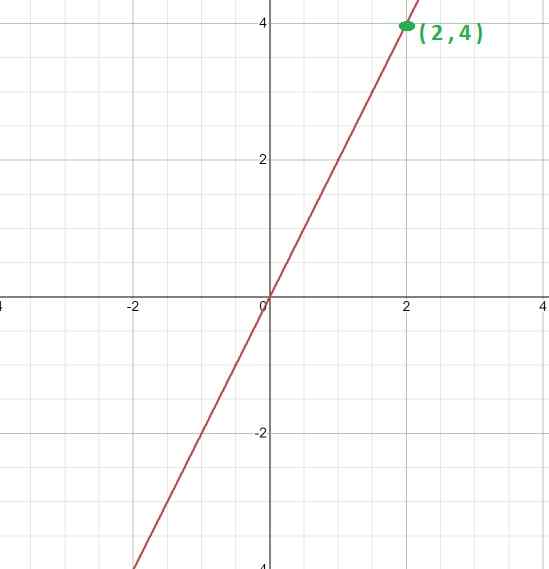
Po pierwsze, wykres jest analizowany, a jego liniowy charakter jest widoczny. Wskazuje to, że jest to funkcja o bezpośredniej proporcjonalności i że wartość k zostanie uzyskana poprzez wyrażenie k = y/x

Następnie wybrany jest określony punkt wykres.

W tej sprawie punkt jest przyjmowany (2, 4). Gdzie możemy ustanowić następujący związek.

K = 4/2 = 2

Tak, że wyrażenie jest zdefiniowane przez funkcję y = kx, która w tej sprawie będzie

F (x) = 2x

Bibliografia

1. Matematyka na energię elektryczną i elektronikę. Dr. Arthur Kramer. Cengage Learning, 27 lipca. 2012
2. Wizja 2020: strategiczna rola badań operacyjnych. N. Ravichandran. Wydawcy Allied, 11 września. 2005
3. Gramatyczna i arytmetyczna wiedza na temat państwa asystenta administracyjnego.e-book. Mad-Eduform
4. Wzmocnienie matematyki pod względem wsparcia i dywersyfikacji programowej: Wspieranie i dywersyfikacja programów nauczania. Mª Lourdes Lázaro Soto. Narcea ediciones, 29 sierpnia. 2003
5. Logistyka i zarządzanie komercyjnymi. Maria José Escudero Serrano. Paraninfo Editions, S.DO., 1 września. 2013