Skończone właściwości, przykłady, ćwiczenia rozwiązane

Jest to rozumiane przez Zestaw skończony Wszystkie ustawione z ograniczoną lub rachunkową liczbą elementów. Przykładami zestawów skończonych są kulki zawarte w torbie, zbiorze domów w sąsiedztwie lub zestawie P utworzone przez dwadzieścia (20) liczb naturalnych:

P = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,13, 14, 16, 17, 18, 19, 20 

Zestaw gwiazd wszechświata jest z pewnością ogromny, ale nie jest to pewne, czy jest skończony czy nieskończony. Jednak zestaw planet układów słonecznych jest skończony.

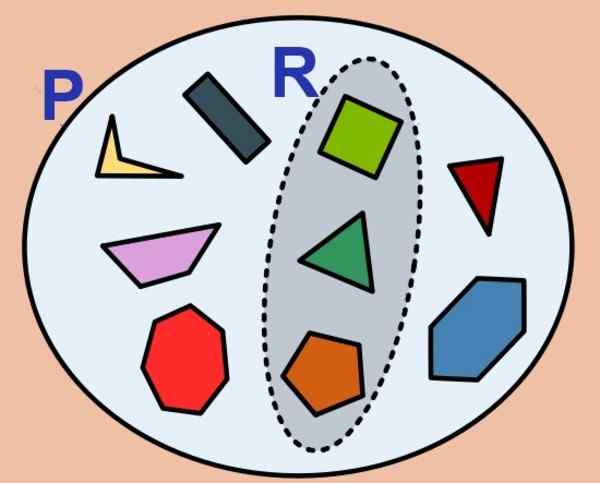
Rysunek 1. Zestaw wielokątów jest skończony, a podzbiór zwykłych. (Wikimedia Commons)

Liczba elementów skończonego zestawu nazywa się jego kardynałem i dla zestawu P Jest to oznaczone tak: karta (P) albo #P. Pusty zestaw ma zerową kartynowość i jest uważany za skończony zestaw.

[TOC]

Nieruchomości

Wśród właściwości skończonych zestawów są następujące:

1- Związek zestawów skończonych powoduje nowy zestaw skończony.

2- Jeśli przechwycono dwa skończone zestaw, jest to nowy zestaw skończony.

3- Podzbiór zestawu skończonego jest skończony, a jego litość jest mniejsza lub równa podzieleniu oryginalnego zestawu.

4- Pusty zestaw to skończony zestaw.

Przykłady

Istnieje wiele przykładów skończonych zestawów. Wśród niektórych przykładów są następujące:

Ustawić M miesięcy roku, które można rozszerzyć w następujący sposób:

M = Styczeń, luty, marzec, kwietnia, maj, czerwca, lipiec, sierpień, wrzesień, październik, listopad, grudzień.

Ustawić S dni tygodnia: S = Poniedziałek, wtorek, środa, czwartek, piątek, sobota, niedziela. Kardynał S to 7.

Może ci służyć: Relacje proporcjonalne: koncepcja, przykłady i ćwiczenia

Ustawić N Z liter hiszpańskiego alfabetu jest to zestaw skończony, ten zestaw jest napisany w ten sposób:

N = A, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, x, y, z i to Kardinalność wynosi 27.

Ustawić V Z samogłosek w języku hiszpańskim jest to podzbiór zestawu:

V ⊂ N Dlatego jest to skończony zestaw.

Zestaw skończony V Rozszerzony sposób, w jaki jest napisane w ten sposób: V = a, e, i, o, u, a jej kardynał wynosi 5.

Zestawy można wyrazić poprzez zrozumienie. Ustawić F Przykładem jest litery słowa „skończony”:

F = x / x to litera słowa „skończony”

Ten zestaw wyrażony szeroko będzie:

F = f, i, n, t, o, którego litość wynosi 5, a zatem jest to zestaw skończony.

Więcej przykładów

Kolory tęczy to kolejny skończony przykład, zestaw C tych kolorów to:

C = czerwony, pomarańczowy, żółty, zielony, cyjan, niebieski, fioletowy, a jego kardynał wynosi 7.

Zestaw faz F Z księżyca jest kolejny skończony przykład:

F = Księżyc w nowiu, pokój uprawny, pełnia księżyca, sala zanika Ten zestaw ma kardynał 4.

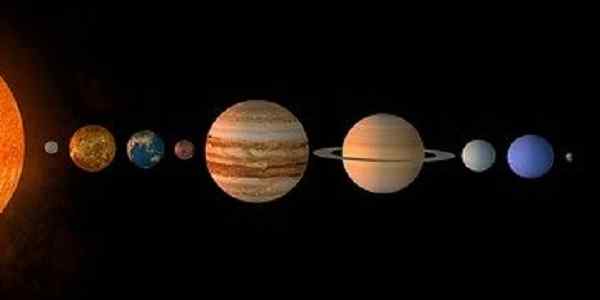Rysunek 2. Planety Układu Słonecznego tworzą skończony zestaw. (Pixabay)

Kolejnym skończonym zestawem jest ten utworzony przez planety układu słonecznego:

P = Mercury, Wenus, Ziemia, Mars, Jowisz, Saturn, Uran, Neptune, Pluton Cardinality 9.

Rozwiązane ćwiczenia

Ćwiczenie 1

Poniższy zestaw jest podany a = x∊ r / x^3 = 27. Wyrażaj to słowami i napisz przez rozszerzenie, wskaż jego kartynowość i powiedz, czy jest skończony.

Może ci służyć: elipsa

Rozwiązanie: Zestaw A jest zbiorem liczb rzeczywistych X, tak że X podniesiony do kostki w rezultacie 27.

Równanie x^3 = 27 ma trzy roztwory: które są x1 = 3, x2 = (-3/2 + 3√3/2 i) i x3 = (-3/2-3√3/2 i). Z trzech rozwiązań tylko x1 jest prawdziwe, a pozostałe dwa są liczbami złożonymi.

Jak mówi definicja zestawu A, że x należy do liczb rzeczywistych, więc rozwiązania w liczbach złożonych nie są częścią zestawu.

Rozszerzony zestaw to:

A = 3, który jest skończonym zestawem kardynałów 1.

Ćwiczenie 2

Napisz symbolicznie (przez zrozumienie) i szeroko zestaw B liczb rzeczywistych, które są większe niż 0 (zero) i mniej lub równe niż 0 (zero). Wskaż swoją kardynał i to, czy jest to skończone.

Rozwiązanie: B = X∊ R / 0 < x <= 0

Ustaw B jest pusty, ponieważ liczba rzeczywista X nie może być jednocześnie większa i mniejsza niż zero, a także 0, a także mniejsza niż 0.

B = , a jego kardynał wynosi 0. Pusty zestaw to zestaw skończony.

Ćwiczenie 3

Podano zestaw rozwiązań określonego równania. Zestaw według zrozumienia jest napisany w ten sposób:

S = x∊ r / (x -3) (x^2 - 9x + 20) = 0

Napisz ten zestaw intensywnie, wskazuj swoją kartynalność i wskaż, czy jest to zestaw skończony.

Rozwiązanie: Po pierwsze, analizując wyrażenie opisujące zestawy, uzyskuje się, że jest to zestaw rzeczywistych wartości x, które są rozwiązaniami równania:

(x -3) (x^2 - 9x + 20) = 0 (*)

Rozwiązaniem tego równania jest x = 3, co jest liczbą rzeczywistą i dlatego należy do S. Ale istnieje więcej rozwiązań, które można uzyskać, poszukując rozwiązań równania kwadratowego:

Może Ci służyć: Dystrybucja F: Charakterystyka i ćwiczenia rozwiązane

(x^2 - 9x + 20) = 0

Poprzednie wyrażenie może uwzględniać następujące:

(x - 4) (x - 5) = 0

Co prowadzi nas do dwóch kolejnych rozwiązań oryginalnego (*) równania, które są x = 4 i x = 5. Krótko mówiąc, równanie (*) ma rozwiązania 3, 4 i 5.

Zestaw S wyrażony szeroko jest taki:

S = 3, 4, 5, który ma kardynał 3, a zatem jest zestawem skończonym.

Ćwiczenie 4

Istnieją dwa zestawy a = 1, 5, 7, 9, 11 i b = x ∊ n / x jest par ^ x x < 10 .

Jawnie napisz zestaw b i znajdź związek z zestawem a. Znajdź także przechwytywanie tych dwóch zestawów i zakończ.

Rozwiązanie: Zestaw B składa się z naturalnych liczb, tak że są one równe, a także są niższe niż wartość 10, dlatego razem B szeroko napisane jest w następujący sposób:

B = 2, 4, 6, 8

Związek zestawu A z zestawem B to:

A U B = 1, 2, 4, 5, 6, 7, 8, 9, 11

A przechwycenie zestawu A z zestawem B jest napisane w ten sposób:

A ⋂ b = = Ø to pusty zestaw. 

Należy zauważyć, że związek i przechwycenie tych dwóch skończonych zestawów prowadzą do nowych zestawów, co z kolei są również skończone.

Bibliografia

1. Źródła, a. (2016). PODSTAWOWA MATEMATYKA. Wprowadzenie do obliczeń. Lulu.com.
2. Garo, m. (2014). Matematyka: równania kwadratowe: jak rozwiązać równanie kwadratowe. Marilù Garo.
3. Haeussler, e. F., I Paul, r. S. (2003). Matematyka administracji i ekonomii. Edukacja Pearsona.
4. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matematyka 1 września. Próg.
5. Precious, c. T. (2005). Kurs matematyki 3o. Progreso redakcyjne.
6. Mathematics 10 (2018). „Przykłady skończonych zestawów”. Źródło: Mathematics10.internet
7. Rock, n. M. (2006). Algebra I jest łatwa! Tak łatwo. Team Rock Press.
8. Sullivan, J. (2006). Algebra i trygonometria. Edukacja Pearsona.
9. Wikipedia. Zestaw skończony. Odzyskane z: jest.Wikipedia.com