Jak uzyskać procent? Przykłady i ćwiczenia

Móc Uzyskaj procent Z kilkoma metodami. Możesz szybko obliczyć 10% dowolnej liczby tylko podczas przenoszenia przecinka dziesiętnego pozycji w lewo. Na przykład 10% ze 100 to 10; 10% z 1000 to 100.

Jeśli chcesz obliczyć bardziej złożone odsetki, takie jak 36% z 25 lub 250% z 20, potrzebne są inne metody. W przypadkach, w których system 10% nie ma zastosowania, można wziąć pod uwagę następujące metodologie.

Rysunek 1. Rabaty z różnymi wartościami procentowymi. Ile się ratujemy?. Źródło: Pixabay.

Termin procent oznacza określoną część każdej setki i odnosi się do operacji arytmetycznej przeprowadzanej w celu znalezienia wspomnianej części. Na przykład 20% („dwadzieścia procent”) jest odczytywane w pesos, oznacza to, że 20 pesos jest dyskontowanych na każde 100 pesos.

Procent służy do obliczenia, która część ogółem reprezentuje kwotę. W takim przypadku suma jest przeniesiona do skali 100, a odsetek informuje o tym, ile, na podstawie tych 100, jest częścią, którą należy obliczyć.

Zobaczmy, jak to się dzieje z tymi przykładami. Po pierwsze, robimy to w postaci ułamka:

• 20% = 20/100
• 5% = 5 /100
• 0,7% = 0,7 / 100
• 100% = 100 /100

Zauważ, że 100% jest równe 1. Ale odsetki można również napisać dziesiętne:

• 20% = 0,20
• 5% = 0,05
• 0,7% = 0,007
• 100% = 1,0

Po wyrażeniu odsetka określonej liczby po prostu Przecinek porusza się Z tych dwóch miejsc po lewej stronie. W procentach, Reguła proporcjonalności:

20% to 20 na 100, dlatego:

20% ze 100 to 20, 20% z 200 to 40, 20% z 300 to 60, 20% z 50 to 10.

Ogólna zasada dla 20 % dowolnej kwoty

20% x to x *(20/100) = x *0,2 = 0,2 *x

Ta zasada może z łatwością rozszerzyć, aby znaleźć inny procent, który jest pożądany. Zobaczmy, jak w poniższej sekcji.

Ćwiczenie rozwiązane w przypadku wzoru w celu obliczenia n% 

Formuła podsumowania jak najszybciej i szybko obliczyć każdy procent N Jest:

N % =(A * n)/100

Na przykład chcesz obliczyć 25% z 400

Następnie n = 25 i a = 400, co daje (400*25)/100 = 100

Przykład

Jaki procent 60 to 24?

Rozwiązanie

To, co jest wymagane, jest równoważne pytanie, jaki jest N% z 60, co daje 24?

Proponujemy ogólną formułę:

60 * N / 100 = 24

Oczyszczamy N Z tą procedurą:

-100, który dzieli na członek iZiédo Równości, idź do członka Prawidłowy mnożenie. 

-I 60, które mnoży się w członku lewy Idź do członka Prawidłowy działowy.

N = 24 *100 /60 = 2400 /60 = 240/6 = 6 *40/6 = 40

Stwierdzono, że 40% z 60 to 24.

Rozwiązane Ćwiczenia obliczania procentowe 

Poniżej znajdują się proste ćwiczenia, aby rozpocząć ćwiczenie wyżej wymienionych.

Może ci służyć: 15 najpopularniejszych legend i mitów

Ćwiczenie 1

Znajdź 50% z 90.

Rozwiązanie

Tutaj x = 90, n = 50 % i wymień:

90 * 50% = 90 * (50 /100) = 4500 /100 = 45 

Jest to dość proste, ponieważ 50 % dowolnej kwoty to połowa tej kwoty, a połowa 90 to 45.

Ćwiczenie 2

Znajdź 30% z 90.

Rozwiązanie

90 * 30% = 90 * (30 /100) = 2700 /100 = 27

Wzrost procentowy

Często w życiu codziennym słuchanie wzrostu czegoś, na przykład wzrostu produkcji, wzrostu wynagrodzenia lub wzrostu produktu. Prawie zawsze jest wyrażany w postaci procentowej.

Na przykład określony produkt kosztował 300 €, ale wzrosła o 30%. Zadajemy sobie pytanie: jaka jest nowa cena produktu?

Pierwszym jest obliczenie części, która odpowiada wzrostowi. Ponieważ wzrost wynosi 30 części 100, więc wzrost wzrostu, w oparciu o pierwotną cenę 300, wynosi trzykrotnie 30 części, czyli 3*30 = 90.

Produkt wzrósł o 90 EUR, więc nowa cena końcowa będzie kosztować wzrost wcześniej:

Nowa cena = stara cena + 90 € = 390 €

Możemy zbudować wzór do obliczenia wzrostu procentowego. Używamy liter, aby symbolizować ceny, takie jak to:

-F to ostateczna wartość

-Siema jest wartością początkową i

-N to wzrost wzrostu.

Przy tych nazwach wartość końcowa zostanie obliczona w ten sposób:

f = i + (i* n / 100)

Ale jak Siema Jest powtarzany w obu kategoriach, można go traktować jako wspólny czynnikAby uzyskać to inne wyrażenie, równie ważne:

F = i * (1 + N / 100)

Sprawdźmy, czy sprawa już została rozwiązana, produkt, który kosztował 300 € i wzrósł o 30%. Dlatego upewniamy się, że formuła działa dobrze:

Cena końcowa = f = 300 € * (1 + 30/100) = 300 € * (1 + 0,3) = 300 * 1,3 = 390 EUR

Ćwiczenie 3

Pracownik zarobił 1500 €, ale został awansowany, a jego pensja wzrosła o 20%. Jaka jest Twoja nowa pensja?

Rozwiązanie

Zastosujmy formułę:

F = 1500 € * (1 + 20/100) = 1500 € * (1 + 0,2) = 1500 € * 1,2 = 1800 EUR

Nowa pensja pracownika wynosi 1800 €.

Procent maleje

W przypadku spadku wzór do obliczenia wartości końcowej F określonej kwoty początkowej Siema które doznało spadku N% Jest:

F = i * (1 - N / 100)

Należy zauważyć, że znak dodatni (+) wzoru w poprzednim rozdziale został zastąpiony znakiem ujemnym (-).

Rysunek 2. Procent rabat. Źródło: Pixabay

Ćwiczenie 4

Produkt oznaczony 800 €, ale otrzymał 15% zniżki. Jaka jest nowa cena produktu?

Rozwiązanie 4

Ostateczna cena według formuły to:

F = 800 € * (1 - 15 /100) = 800 € * (1 - 0,15) = 800 € * (0,85) = 680 EUR

Ostateczna cena z 15% zniżką wynosi 680 €, co stanowi oszczędność 120 €.

Kolejne wartości procentowe

Pojawia się, gdy pewna ilość cierpi na procentową zmienność, a następnie nałożona jest kolejna, również procent. Na przykład produkt, który z rzędu miał dwa procentowe rabaty. Innym przykładem jest pracownik, który miał dwa kolejne podwyżki wynagrodzeń.

Może ci służyć: ważniejsza działalność gospodarcza w Jukatanie

- Kolejny wzrost procentowy

Podstawa rozwiązań tych przypadków jest taka sama jak unikalne wzrosty, ale należy wziąć pod uwagę, że drugi wzrost procentowy jest przeprowadzany na końcowej wartości pierwszego wzrostu.

Załóżmy, że produkt, który wzrósł najpierw o 10%, a następnie 5%. Niepoprawne jest stwierdzenie, że podniósł wzrost o 15%, w rzeczywistości było to więcej niż ten procent.

Obowiązują formuły dla wartości końcowej:

-Najpierw oblicza się końcową wartość pierwszego wzrostu N1%

f1 = i + i * n1 / 100

-A następnie, aby znaleźć ostateczną wartość drugiego wzrostu N2%, ostateczna wartość F1 jest traktowana jako wartość początkowa. Dlatego:

F2 = f1 + f1 * n2 /100 

Ćwiczenie 5

Książka pierwotnie kosztowała 55 EUR, ale ze względu na jej sukces i wysoki popyt, doznała dwóch kolejnych wzrostów w pierwotnej cenie. Pierwszy wzrost wynosił 10%, a drugi z 20%. Jaka jest ostateczna cena książki?

Rozwiązanie

-Pierwszy wzrost:

F1 = 55 € * (1 + 10 /100) = 55 * 1,1 = 60,5 €

-Drugi wzrost

F2 = 60,5 € * (1 + 20/100) = 60,5 € * 1,2 = 72,6 EUR

Ostateczna cena wynosi 72,6 €.

Ćwiczenie 6

W odniesieniu do poprzedniego ćwiczenia. Dwa kolejne wzrosty: do jakiego odsetka unikalnego wzrostu w porównaniu z oryginalną ceną książki odpowiadają?

Rozwiązanie

Jeśli nazwiemy N% do odsetka unikalnego wzrostu, formuła, która odnosi ten unikalny wzrost procentowy do pierwotnej wartości, a ostateczną wartość to:

F2 = i *(1 + n / 100) 

To jest do powiedzenia:

72,6 € = 55 € + 55 € * (N / 100)

Oczyszczając wzrost wzrostu n% = (n /100), mamy:

(N / 100) = (72,6 € - 55 €) / 55 € = 17.6 € / 55 € = 0,32

Dlatego:

N = 0,32 * 100 = 32

W cenie książki zastosowano całkowity wzrost o 32%. Należy zauważyć, że wzrost ten jest większy niż suma dwóch kolejnych wzrostów procentowych.

- Kolejne zniżki procentowe

Pomysł jest podobny do pomysłu kolejnego wzrostu procentowego. Drugi procent rabatu należy zawsze stosować do ostatecznej wartości pierwszej rabatu, spójrzmy na przykład:

Ćwiczenie 7

10% zniżki, a następnie drugi rabat w wysokości 20% na obiekcie, do którego unikalny procentowy rabat jest równoważny?

Rozwiązanie

-Pierwsza zniżka:

F1 = i - i * n1 / 100  

-Druga zniżka

F2 = f1 - f1 * n2 / 100

Zastąpienie pierwszego równania w drugim pozostaje:

f2 = (i - i * n1 / 100) - (i - i * n1 / 100) * n2 / 100

Rozwijając to wyrażenie, otrzymujemy:

f2 = i - i* n1 / 100 - i* n2 / 100 + i* (n1 / 100) (n2 / 100) 

Rysowanie wspólnego czynnika Siema:

f2 = i * (1- n1% - n2% + n1% * n2%)

Wreszcie wartości procentowe wskazane w pytaniu zostaną zastąpione:

F2 = i * (1 - 10% - 20% + 10% * 20%) = i * (1 - 0,1 - 0,2 + 0,1 * 0,2)

f2 = i * (1 - 0,3 + 0,02) = i * (0,72) = i * (1 - 0.28) = i * (1 - 100 /100) = i * (1 - 28%)

Innymi słowy, kolejne rabaty w wysokości 10% i 20% odpowiadają unikalnej 28% zniżki.

Ćwiczenia zaawansowane

Wypróbujmy te ćwiczenia tylko wtedy, gdy pomysły poprzednich były wystarczająco jasne.

Może ci służyć: łatwe i piękne pokrowce geograficzne, okładki, obrazy

Ćwiczenie 8

Podstawa trójkąta mierzy 10 cm i wysokość 6 cm. Jeśli długość podstawy spadnie o 10%. W jakim odsetku należy zwiększyć wysokość, aby obszar trójkąta się nie zmienił?

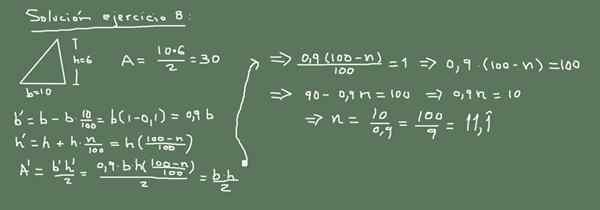Rysunek 3. Alternatywne rozwiązanie ćwiczeń 8. Przygotowane przez f. Zapata.

Rozwiązanie 8

Oryginalny obszar trójkąta to:

A = (10 cm * 6 cm) / 2 = 30 cm²

Teraz, jeśli podstawa maleje o 10%, jego nowa wartość wynosi:

Nowa baza = 10 - (10/100) x 10 = 9 cm.

Nowa wartość wysokości wynosi x, a oryginalny obszar musi być utrzymywany niezmieniony, aby:

(9 cm * x) /2 = 30 cm²

Następnie wartość x jest wyczyszczana jako:

X = 60 cm² / 9 cm = (20/3) cm = 6666 cm

Co oznacza wzrost o 0,666 w porównaniu z pierwotną wartością. Zobaczmy teraz, jaki procent tego reprezentuje:

6 666 = 6 + (6 * N/100) 

6 666 -6 = 6 * N/100

0.666 = 6 * n/100

N/100 = 0,111

N = 11,1

Odpowiedź brzmi: wysokość należy zwiększyć o 11,1%, aby obszar trójkąta pozostał taki sam.

Ćwiczenie 9

Jeśli pensja wzrośnie o 20%, ale zniżki podatkowe o 5%, jaki jest prawdziwy wzrost, który otrzymuje pracownik?

Rozwiązanie 

Najpierw obliczamy wzrost N1%:

f1 = i + i * n1 / 100

Następnie stosujemy rabat N2%:

F2 = f1 - f1 * n2 / 100

Pierwsze równanie zostało zastąpione w drugim:

f2 = i + i * n1 / 100 - (i + i * n1 / 100) * n2 / 100

Poprzednie wyrażenie rozwija się:

f2 = i + i * n1 / 100 - i * n2 / 100 - i * (n1 / 100) * (n2 / 100)

Wreszcie jest usuwany Siema Wspólny czynnik i wartości N1 = 20 i N2 = 5, które pojawiają się w instrukcji, zostały zastąpione:

F2 = i (1 + 0,2 - 0,05 - 0,2* 0,05) = i* (1 + 7/50) = i* (1 + 14/100) = i* (1 + 14%)

Pracownik otrzymał wzrost netto o 14%.

Ćwiczenie 10

Zdecyduj, co jest najwygodniejsze między tymi dwiema opcjami:

i) nabywaj t -shirts z 32 % zniżką.

Ii) Kup 3 wysypki za cenę 2.

Rozwiązanie 

Analizujemy każdą opcję osobno, a następnie wybieramy najbardziej ekonomiczne:

i) Niech X będzie obecną ceną koszuli, 32 % rabat stanowi ostateczną cenę XF:

Xf = x - (32/100) x = x - 0.32x = 0.68x

Na przykład zakup 3 koszul oznacza wydawanie 3 x 0.68 x = 2.04X

ii) Jeśli x jest ceną koszuli, za 3 koszule po prostu zapłacisz 2x.

Załóżmy, że koszula jest warta 6 euro, z 32 % zniżką byłaby warta 4.08 euro. Kup 1 -shirt nie jest ważną opcją w ofercie 3 × 2. Więc jeśli chcesz kupić tylko 1 koszulę, zniżka jest preferowana.

Ale jeśli chcesz kupić za dziesiątki, oferta 3 × 2 jest tylko trochę tańsza. Na przykład 6 wyszyt t ze zniżką wychodzi na 24.48 euro, podczas gdy z ofertą 3 × 2 kosztowałoby 24 euro

Bibliografia

1. Łatwa klasa. Procent. Źródło: Classroom.com
2. Baldor a. 2006. Praktyczna arytmetyka teoretyczna. Edycje kulturalne.
3. Educów dzieci. Jak nauczyć się obliczać wartości procentowe. Odzyskane z: Educapeques.com
4. Gutiérrez, g. Notatki z matematyki finansowej. Odzyskane z: csh.Izt.Uam.MX
5. Inteligentne kleszcze. Procent: co jest i jak obliczane. Odzyskany z: Smartick.Jest