Proces cyklu Brayton, wydajność, zastosowania, ćwiczenia

On Cykl Brayton Jest to cykl termodynamiczny składający się z czterech procesów i dotyczy ściśliwego płynu termodynamicznego jak gaz. Jego pierwsze wzmianki pochodzi z końca XVIII wieku, chociaż spędził trochę czasu, zanim wychował go James Joule. Dlatego jest również znany jako cykl dżur.

Składa się z następujących etapów, które są dogodnie zilustrowane na schemacie ciśnienia - objętość Ryc. 1: Kompresja adiabatyczna (nie wymieniane jest ciepło), rozszerzanie izobaryczne (występuje pod stałe ciśnienie), rozszerzanie adiabatyczne (nie wymieniane jest ciepło) i kompresja izobaryczna) i kompresja izobaryczna) (występuje pod stałym ciśnieniem).

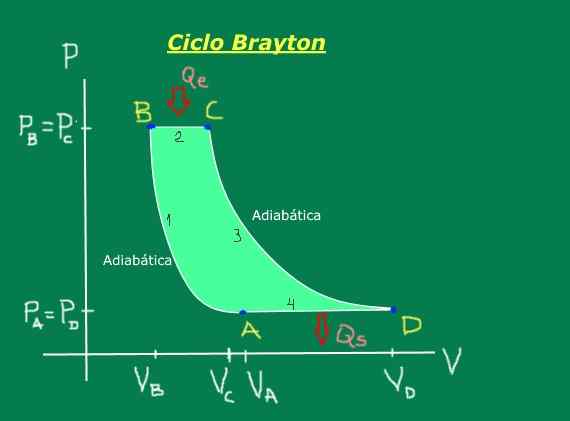Rysunek 1. Cykl Brayton. Źródło: Self Made.

[TOC]

Proces i opis

Cykl Brayton jest idealnym cyklem termodynamicznym, który najlepiej zastosować do wyjaśnienia termodynamicznego funkcjonowania turbin gazowych i miesza paliwo powietrzne, stosowane do wytwarzania energii elektrycznej i w silnikach lotniczych.

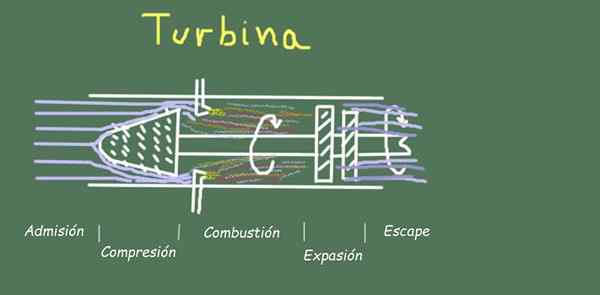Rysunek 2. Schemat turbiny i etapy przepływu. Źródło: Self Made.

Na przykład w obsłudze turbiny istnieje kilka etapów przepływu gazu operacyjnego, które zobaczymy poniżej.

Wstęp

Składa się z wlotu powietrza w temperaturze i ciśnieniu środowiskowym z powodu otwarcia turbiny.

Kompresja

Powietrze jest sprężane przez wirujące palety przeciwko innym ustalonym w odcinku sprężarki turbiny. Ta kompresja jest tak szybka, że ​​praktycznie nie ma wymiany ciepła, więc jest modelowana w procesie AB Cycle Brayton. Powietrze po wyjściu sprężarki podniosło jej ciśnienie i temperaturę.

Spalanie

Powietrze jest mieszane z gazem propanowym lub paliwem sproszkowanym, które jest wprowadzane przez wtryskiwacze komory spalania. Mieszanina powoduje chemiczną reakcję spalania.

Ta reakcja jest tą, która zapewnia ciepło, które zwiększa temperaturę i energię kinetyczną cząstek gazu, które rozszerzają się w komorze spalania przy stałym ciśnieniu. W cyklu Brayton ten etap jest modelowany z procesem BC, który występuje pod stałym ciśnieniem.

Ekspansja

W odcinku samej turbiny powietrze nadal rozwija się wbrew paletom turbin. Na tym etapie powietrze obniża jego temperaturę, ale bez wymiany ciepła praktycznie w środowisku.

W cyklu Braytona ten krok jest symulowany jako CD procesu ekspansji adiabatycznej. Część pracy turbiny jest przenoszona do sprężarki, a druga służy do przenoszenia generatora lub śmigła.

Wydechowy

Wychodzące powietrze jest pod stałym ciśnieniem równym środowisku i daje ciepło na ogromną masę powietrza zewnętrznego, więc w krótkim czasie wymaga tej samej temperatury powietrza wlotowego. W cyklu Brayton ten etap jest symulowany z procesem stałego ciśnienia, zamykając cykl termodynamiczny.

Wydajność oparta na temperaturze, ciepła i ciśnienia

Proponujemy obliczenie wydajności cyklu Braytona, od którego zaczynamy od definicji tego samego.

W maszynie termicznej wydajność jest zdefiniowana jako praca netto wykonana przez maszynę podzieloną przez dostarczoną energię cieplną.

Może ci służyć: odbicie światła

Pierwsza zasada termodynamiki stwierdza, że ​​ciepło netto przyczyniło się do gazu w procesie termodynamicznym, jest równe zmiany energii wewnętrznej gazu plus prace wykonane przez to samo.

Ale w pełnym cyklu zmienność energii wewnętrznej jest nieważna, więc ma to, że ciepło netto przyczyniane do cyklu jest równe wykonanej pracy netto.

Nadchodzące ciepło, ustępujące ciepło i wydajność

Poprzednie wyrażenie pozwala nam pisać wydajność na podstawie pochłanianego lub przychodzącego ciepła (Positvo) i przypisanego lub wychodzącego QS (ujemne).

Ciepło i ciśnienie w cyklu Brayton

W cyklu Braytona ciepło wchodzi w proces izobaryczny BC i pojawia się w procesie izobarycznym.

Zakładając, że bez stałego ciśnienia dostarczanego z wrażliwym ciepłem, które w procesie BC, jego temperatura wzrasta z TB do TC zgodnie z następującą relacją:

Gdzie CP Jest to pojemność cieplna przy stałym ciśnieniu.

Wychodzące ciepło QS Można go obliczyć podobnie przez następującą zależność, która dotyczy procesu pod stałym ciśnieniem:

Zastępowanie tych wyrażeń w wyrażeniu, które daje nam wydajność oparte na nadchodzącym ciepło i wychodzącym ciepło, dzięki czemu uzyskuje się istotne uproszczenia, uzyskuje się następujący związek wydajności:

W rezultacie wydajność jest niezależna od masy powietrza, która przechodzi przez turbinę.

Uproszczony wynik

Możliwe jest uproszczenie poprzedniego wyniku, jeśli weźmiemy pod uwagę PA = PD I? PB = PC Ponieważ procesy AD i BC są isobárica, to znaczy pod tym samym ciśnieniem.

Ponadto, ponieważ procesy AB i CD są adiabatyczne, relacja Poissona dla obu procesów jest spełniona:

Gdzie Gamma reprezentuje iloraz adiabatyczny, to znaczy iloraz między pojemnością cieplną przy stałym ciśnieniu a pojemnością cieplną przy stałej objętości.

Korzystając z tych relacji i związku równania stanu idealnego gazu, możemy uzyskać alternatywne wyrażenie relacji Poissona:

Jak wiemy PA = PD I? PB = PC Zastępując i dzieląc członka na członka, uzyskuje się następujący związek między temperaturami:

Jeśli każdy element poprzedniego równania jest odjęta od urządzenia, różnica jest rozwiązana, a warunki ustalone, można wykazać, że:

Tak aby wydajność można było zapisać jako funkcję temperatury powietrza w temperaturze wlotu i powietrza na końcu procesu kompresji AB.

Wydajność w zależności od współczynnika ciśnienia

Wyrażenie uzyskane dla wydajności cyklu Braytona w oparciu o temperatury można przepisać do sformułowania na podstawie współczynnika ciśnienia przy wyjściu i wejściu do sprężarki.

Osiąga się to, jeśli związek Poissona między punktami A i B jest znany w zależności od ciśnienia i temperatury, uzyskując, że wydajność cyklu jest wyrażona w następujący sposób:

Może ci służyć: presja względna: wzór, sposób, w jaki jest obliczane, przykłady, ćwiczenia

Będąc ilorazem między PB i PA.

Typowy współczynnik ciśnienia wynosi 8. W tym przypadku cykl Brayton ma teoretyczną wydajność 45%.

Aplikacje

Cykl Brayton jako model dotyczy turbin gazowych stosowanych w roślinach termoelektrycznych w celu przesuwania generatorów wytwarzających energię elektryczną.

Jest to również model teoretyczny, który dobrze pasuje do działania silników turboherowych, które są używane w samolotach, ale wcale nie ma zastosowania w turboreaktorach samolotów.

Kiedy jest zainteresowany.

Rysunek 3. Silnik turbofanu bardziej wydajny niż turboreaktor. Źródło: Pixabay

Z drugiej strony w turboreaktorach samolotów nie jest zainteresowane.

Przeciwnie, jest zainteresowane.

Rozwiązane ćwiczenia

-Ćwiczenie 1

Turbina gazowa stosowana w roślinach termoelektrycznych ma ciśnienie w gniazdku sprężarki 800 kPa. Temperatura przychodzącego gazu jest środowisko i wynosi 25 Celsjusza, a ciśnienie wynosi 100 kPa.

W komorze spalania temperatura wzrasta do 1027 Celsjusza, aby wejść do turbiny.

Określ wydajność cyklu, temperaturę gazu ze sprężarki i temperatura gazu w wylotu turbiny.

Rozwiązanie

Ponieważ mamy ciśnienie gazowe na wyjściu sprężarki i wiemy, że ciśnienie wejściowe jest ciśnieniem atmosferycznym, więc możliwe jest uzyskanie współczynnika ciśnienia:

R = Pb / PA = 800 kPa / 100 kPa = 8

Ponieważ gaz, z którym działa turbina, jest mieszaniną powietrza i gazu propanu, stosuje się następnie współczynnik adiabatyczny dla idealnego gazu dwuatomicznego, to znaczy gamma 1,4.

Wydajność zostanie następnie obliczona w ten sposób:

Gdzie zastosowaliśmy związek, który zapewnia wydajność cyklu Braytona w zależności od współczynnika ciśnienia w sprężarce.

Obliczanie temperatury

Aby określić temperaturę przy wyjściu sprężarki lub co jest taka sama, z jaką gaz wchodzi do komory spalania, stosujemy stosunek związku z wejściem sprężarki i temperaturami wyjścia.

Jeśli usuniemy temperaturę TB z tego wyrażenia, uzyskujemy:

Innymi słowy, temperatura przed podstępem wynosi 804,12 Celsjusza.

W miarę ćwiczeń musimy po spalaniu temperatura wzrasta do 1027 Celsjusza, aby wejść do turbiny. Część energii cieplnej gazu służy do przemieszczania turbiny, więc temperatura przy jej wyjściu musi być niższa.

Może ci służyć: zastosowania energii, mocy, siły, koncepcji pracy

Aby obliczyć temperaturę przy wyjściu turbiny, wykorzystamy wcześniej stosunek między temperaturą:

Stamtąd usuwamy TD, aby uzyskać temperaturę w wylotu turbiny. Po wykonaniu obliczeń uzyskana temperatura wynosi:

TD = 143,05 Celsjusza.

-Ćwiczenie 2

Turbina gazowa podąża za cyklem Brayton. Presja między wyjazdem a wejściem do sprężarki wynosi 12.

Zakładaj temperaturę otoczenia 300 K. Jako dodatkowe dane wiadomo, że temperatura gazu po spalaniu (przed wejściem do turbiny) wynosi 1000k.

Określić temperaturę przy wyjściu sprężarki i temperaturę w gniazdku turbiny. Określ także, ile kilogramów gazu krążą przez turbinę w ciągu każdej sekundy, wiedząc, że jego moc wynosi 30 kW.

Zakładaj ciepło właściwe gazu jako stałe i weź jego wartość w temperaturze pokojowej: CP = 1 0035 J / (kg K).

Załóżmy również, że wydajność kompresji w sprężarce i dekompresji w turbinie wynosi 100%, co jest idealizacją, ponieważ w praktyce zawsze występują straty.

Rozwiązanie

Aby określić temperaturę przy wyjściu sprężarki, znaną temperaturę przy wejściu, musimy pamiętać, że jest to kompresja adiabatyczna, więc można zastosować związek Poissona dla procesu AB.

W ten sposób uzyskujemy, że temperatura TB przy wyjściu sprężarki jest podana przez:

W ten sam sposób dekompresja gazów przecinających turbinę jest procesem adiabatycznym, który odpowiadałby procesie cyklu Brayton. Dlatego możemy zastosować stosunek Poissona, aby uzyskać temperaturę wylotu turbiny.

W przypadku każdego cyklu termodynamicznego praca netto zawsze będzie równa ciepło netto wymieniane w cyklu.

W poprzedniej relacji, jakim jest nadchodzące (dodatnie) ciepło i QS wychodzące (ujemne) ciepło. W cyklu Braytona wymiany te występują procesy BC i DA, oba izobáricas.

Prace netto na cykl operacji można następnie wyrazić w zależności od masy gazu, która krążyła w tym cyklu i temperaturach.

W tym wyrażeniu M Jest to masa gazu krążyła przez turbinę w cyklu operacyjnym i CP Ciepło właściwe.

Jeśli weźmiemy pochodną w odniesieniu do czasu poprzedniego wyrażenia, uzyskujemy średnią moc netto na podstawie przepływu masy.

Clearing M PUNKT, i zastępując temperatury, moc i pojemność cieplną gazu uzyskujemy przepływ masowy 1578,4 kg/s.

Bibliografia

1. Alfaro, J. Cykle termodynamiczne. Odzyskane z: fis.Puc.Cl.
2. Fernández J.F. Cykl Brayton. Turbina gazowa. LUB.T.N. (Mendoza). Odzyskane z: edutecne.Utn.Edu.ar.
3. Uniwersytet Sevilla. Dział fizyki. Cykl Brayton. Odzyskany z: Laplace.nas.Jest.
4. National Experimental University of the Táchira. Zjawiska transportowe. Cykle energii gazowej. Odzyskane z: uet.Edu.Iść.
5. Wikipedia. Cykl Brayton. Odzyskane z: Wikiwand.com
6. Wikipedia. Turbina gazowa. Odzyskane z: Wikiwand.com.