Sprzężony dwumianowy sposób, w jaki jest rozwiązany, przykłady, ćwiczenia

A Sprzężony dwumian Z innej dwumianowej to taki, w którym różnią się jedynie znakiem operacji. Dwumian, jak sama nazwa wskazuje, jest strukturą algebraiczną, która składa się z dwóch terminów.

Niektóre przykłady dwumianowe to: (A + B), (3M - N) I (5x - y). A ich odpowiednie sprzężone dwumianowe są: (a - b), (-3 m - n) i (5x + y). Jak można zobaczyć natychmiast, różnica dotyczy znaku.

Rysunek 1. Dwumianowy i jego sprzężony dwumian. Mają te same warunki, ale różnią się znakiem. Źródło: f. Zapata.

Dwumianek pomnożony przez jego koniugat powoduje niezwykły produkt, który jest często używany w algebrze i nauce. Wynikiem mnożenia jest odjęcie kwadratów warunków oryginalnego dwumianowego.

Na przykład, (X - y) Jest dwumianowy, a jego koniugat jest (x + y). Następnie produktem dwóch dwumianów jest różnica kwadratów terminów:

(X - y).(x + y) = x² - I²

[TOC]

Jak rozwiązany jest sprzężony dwumianowy?

Reguła wypowiedziana z sprzężonymi dwumianami jest następująca: 

Produkt dwóch dwumianów sprzężonych jest równy kwadratowi pierwszego okresu minus kwadrat drugiego terminu. Ten wynik nazywa się różnicą kwadratową.

Jako przykład zastosowania zaczniemy od zademonstrowania poprzedniego wyniku, który można wykonać przy użyciu właściwości dystrybucyjnej produktu w odniesieniu do sumy algebraicznej.

(x - y) (x + y) = x.x + x.i i.X - y.I

Poprzednie mnożenie uzyskano po tych krokach:

- Pierwszy okres pierwszej dwumianowej jest mnożony przez pierwszy okres drugiego

- Potem pierwszy z pierwszego, po drugie

- Następnie drugi z pierwszego po raz pierwszy 

- Wreszcie drugi z pierwszego drugiego drugiego.

Może ci służyć: algebra wektorowa

Teraz dokonajmy niewielkiej zmiany za pomocą własności przemiennej: I.x = x.I. Pozostaje tak:

(x - y) (x + y) = x.x + x.y - x.i i.I

Ponieważ istnieją dwa równe warunki, ale poza tym (podświetlone w kolorze i podkreślone), są one anulowane i uproszczone:

(x - y) (x + y) = x.X - y.I

Wreszcie stosuje się, że mnożenie liczby samodzielnie jest równoważne podnoszeniu jej kwadratowego, więc X.x = x² i również I.y = y².

W ten sposób, co wskazano w poprzednim rozdziale, że produktem sumy dla jej różnicy jest różnica kwadratów:

(X - y).(x + y) = x² - I²

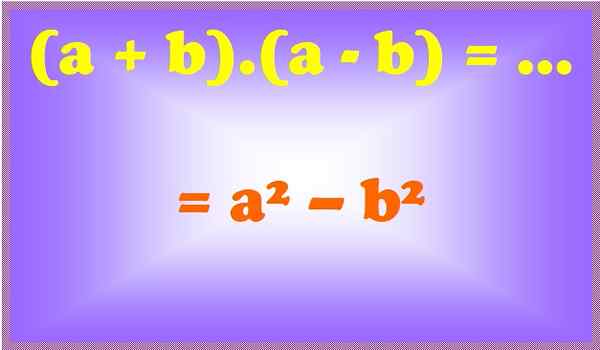Rysunek 2. Suma jego różnicy to różnica kwadratów. Źródło: f. Zapata.

Przykłady

- Sprzężone dwumianki różnych wyrażeń

Przykład 1

Znajdź koniugat (i² - 3y).

Odpowiedź: (I² + 3y)

Przykład 2

Zdobądź produkt (i² - 3y) dla jego koniugatu.

Odpowiedź: (I² - 3y) (i² + 3y) = (i²)² - (3y)² = y⁴ - 3² I² = y⁴ - 9Y²

Przykład 3

Opracuj produkt (1 + 2a).(2a -1).

Odpowiedź: Poprzednie wyrażenie jest równoważne (2a + 1).(2a -1), to znaczy odpowiada iloczynowi dwumianowej dla jego koniugatu.

Wiadomo, że iloczyn dwumianowy dla jego sprzężonego dwumianu jest równy różnicy kwadratów terminów dwumianowych:

(2a + 1) (2a -1) = (2a)² - 1² = 4 a² - 1

Przykład 4

Napisz produkt (x + y + z) (x - y - z) jako różnica kwadratów.

Odpowiedź: Możemy asymilować trynomile przed formą sprzężonych dwumianów, staranne wykorzystanie nawiasów i nawiasów kwadratowych:

(x + y + z) (x - y - z) = [x + (y + z)] [x - (y + z)]

W ten sposób można zastosować różnicę kwadratów:

(x + y + z) (x - y - z) = [x + (y + z)].[x - (y+z)] = x² - (Y+z)²

Przykład 5

Wyrażaj produkt (m² - M -1).(M² + m -1) jako różnica w kwadratach.

Może ci służyć: 120 dzielników

Odpowiedź: Poprzednie wyrażenie jest iloczynem dwóch trynomialnych. Po pierwsze, należy go przepisać jako iloczyn dwóch sprzężonych dwumilek:

(M² - M -1) (m² + m -1) = (m² - 1 - m) (m² -1 + m) = [(m² -1) - m].[(M² -1) +m)]

Stosujemy fakt, że iloczyn dwumianowego przez jego koniugat jest kwadratową różnicą jego terminów, jak wyjaśniono:

[(M² -1) - m].[(M² -1) +m)] = (m² -1)² - M²

Ćwiczenia

Jak zawsze, zaczyna się od najprostszych ćwiczeń, a następnie poziom złożoności.

- Ćwiczenie 1

Escrida (9 - a²) Jako produkt.

Rozwiązanie

Najpierw przepisujemy wyrażenie jako różnica kwadratów, aby zastosować to, co wyjaśniono wcześniej. Dlatego:

(9 - a²) = (3² - Do²)

Natychmiast uwzględniamy, co jest równoważne pisanie tej różnicy kwadratów jako produktu, zgodnie z żądaniem w oświadczeniu:

(9 - a²) = (3² - Do²) = (3 + a) (3 -a)

- Ćwiczenie 2

Forestize 16x² - 9Y⁴.

Rozwiązanie

Czynnik wyrażenie oznacza napisanie go jako produktu. W takim przypadku konieczne jest wcześniej przepisanie wyrażenia, aby uzyskać różnicę kwadratów.

Nie jest to trudne, ponieważ starannie obserwując, wszystkie czynniki są idealnymi kwadrami. Na przykład 16 jest kwadratem 4, 9 jest kwadratem 3, I⁴ jest kwadratem I² I X² jest kwadratem X:

16x² - 9Y⁴  = 4²X² - 3²I⁴ = 4²X²  - 3²(I²)²

Zatem to, co już wiemy, jest stosowane: różnica w kwadratach jest produktem sprzężonych dwumianów:

(4x)² - (3 i²)² = (4x - 3 i²) . (4x + 3 i²)

- Ćwiczenie 3

Napisz (a - b) jako produkt dwumianowy

Rozwiązanie

Poprzednia różnica powinna być napisana jako różnice kwadratowe

(√A)² -(√b)²

Następnie stosuje się, że różnica w kwadratach jest iloczynem sprzężonych dwumianów

Może ci służyć: redukcja podobnych terminów

(√A - √b) (√A + √b)

- Ćwiczenie 4

Jednym z zastosowań sprzężonego dwumianowego jest racjonalizacja wyrażeń algebraicznych. Procedura polega na wyeliminowaniu korzeni mianownika wyrażenia ułamkowego, co przy wielu okazjach ułatwia operacje. Poproszono o użycie sprzężonego dwumianowego do zracjonalizacji następującego wyrażenia:

√ (2 -x) / [√3 - √ (2+x)]]]

Rozwiązanie

Pierwszym z nich jest identyfikacja sprzężonego dwumianowego mianownika: [√3 + √ (2 + x)]]].

Teraz mnożymy licznik i mianownik oryginalnego wyrażenia przez sprzężone dwumianowe:

√ (2 -x) [√3+√ (2+x)] /[√3 - √ (2+x)].[√3 + √ (2 + x)]

W mianowniku poprzedniego wyrażenia rozpoznajemy iloczyn różnicy przez sumę, o której już wiemy, że odpowiada różnicy kwadratów dwumianowych:

√ (2-x) .[√3 + √ (2 + x)] /(√3)² - [√ (2+x)]² 

Uproszczenie mianownika to:

√ (2-x).[√3+√ (2+x)] / [3 - (2+x)] = √ (2 -x). [√3 + √ (2 + x)] / (1 - x)

Teraz dbamy o licznik, do którego zastosujemy własność dystrybucyjną produktu w odniesieniu do sumy:

√ (2-x) .[√3 + √ (2 + x)] / (1 - x) = √ (6-3x) + √ [(2 -x) (2 + x)] / (1 - x)

W poprzednim wyrażeniu rozpoznajemy iloczyn dwumianowego (2-x) dla jego koniugatu, który jest niezwykłym produktem równym różnicy kwadratów. W ten sposób ostatecznie uzyskuje się racjonalizowane i uproszczone wyrażenie:

[√ (6-3x) + √ (4-x²)] / (1 - x)

- Ćwiczenie 5

Opracuj następujący produkt, wykorzystując właściwości sprzężonego dwumianowego:

[2^{(x + 3y)} - 3^{(x - 3y)}].[2^{(x + 3y)} + 3^{(x - 3y)}]

Rozwiązanie

4^{(2x + 6y)} - 9^{(2x - 6y)} = 4a^(2x) .Do^(6y) - 9^(2x) .Do^(-6Y)= [4a^(6y) - 9^(-6Y)] .Do^(2x)

Uważny czytelnik zauważy wspólny czynnik, który został wyróżniony w kolorze.

Bibliografia

1. Baldor, a. 1991. Algebra. Wenezuelskie redakcje kulturalne.DO.
2. González J. Koniugowane ćwiczenia dwumianowe. Odzyskane z: Akademia.Edu.
3. Matematyka Alex. Niezwykłe produkty. Odzyskany z YouTube.com.
4. Math2me. Sprzężone dwumianki/ godne uwagi produkty. Odzyskany z YouTube.com.
5. Sprzężone produkty dwumianowe. Odzyskane z: LMS.Colbachenlinea.MX.
6. Wita. Sprzężone dwumianki. Odzyskane z: YouTube.com.