Definicja platformy czynnikowej, formuły i ćwiczenia

On Platforma czynnikowa Jest to prosta maszyna, która składa się z układu koła pasowego z mnożnikiem siły. W ten sposób możesz podnieść obciążenie, stosując tylko odpowiednik ułamka wagi na wolnym końcu liny.

Składa się z dwóch zestawów kół pasowych: jednego, który jest ustalony na podporę, a drugi, który wywiera wynikową siłę na obciążenie. Koła pasowe są zamontowane na ogólnie metalicznej ramie, która je trzyma. 

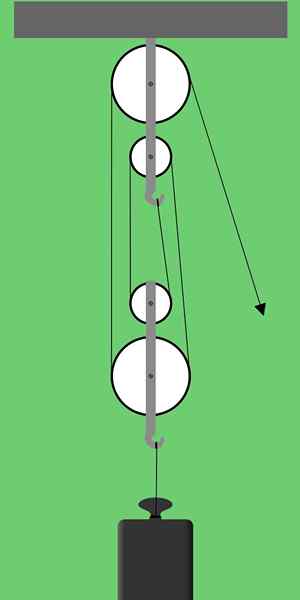
Rysunek 1. Schemat platformy czynnikowej. Źródło: Pixabay

Rycina 1 pokazuje platformę czynnikową, która składa się z dwóch grup dwóch kół pasowych każdy. Nazywane są również tego rodzaju układy koła pasowe REG albo Polipasty.

[TOC]

Właściwe formuły czynnikowe

Przypadek 1: Mobilny koło pasowe i ustalone

Aby zrozumieć, dlaczego ten układ mnoży wywierany przez siłę, zaczniemy od najprostszego przypadku, składającego się z stałego i mobilnego koła pasowego.

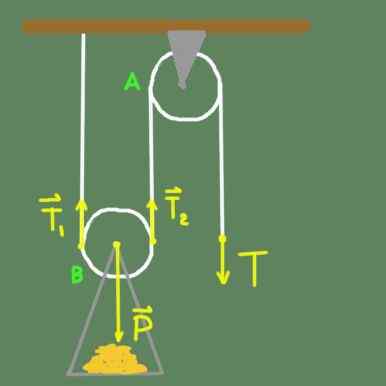Rysunek 2. Dwa platforma koła pasowa.

Na rycinie 2 mamy stały koło pasowe na dachu przez podporę. Koło pasowe A może swobodnie obracać się wokół jego osi. Mamy również ko pasmowe B, który ma stałe podpórkę do osi koła pasowego, w którym obciążenie jest umieszczane. Koło pasowe B, oprócz możliwości swobodnego obracania się wokół jej osi, ma możliwość poruszania się pionowo.

Załóżmy, że jesteśmy w sytuacji równowagi. Rozważ siły działające na koło pasowe B. Oś B -Pulley obsługuje całkowitą wagę P, która jest skierowana w dół. Gdyby to była jedyna siła na koła pasowego B, ale wiemy, że lina, która przechodzi przez ten koło pasowe, również wywiera dwie siły, które są T1 i T2, które są skierowane w górę.

W celu równowagi translacyjnej dwie siły w górę muszą być takie same z wagą, która podtrzymuje oś koła pasowego B.

T1 + T2 = P

Ale ponieważ koło pasowe B znajduje się również w równowadze obrotowej, a następnie T1 = T2. Siły T1 i T2 pochodzą z napięcia zastosowanego do liny, zwanej t.

Może ci służyć: model atomowy Bohr

Dlatego t1 = t2 = t. Zastąpienie w poprzednim równaniu pozostaje:

T + t = p

2t = p

Wskazując, że napięcie stosowane do liny wynosi zaledwie połowę wagi:

T = p/2

Na przykład, gdyby obciążenie wynosiło 100 kg, wystarczyłoby zastosowanie siły 50 kg na wolnym końcu liny, aby podnieść obciążenie ze stałą prędkością.

Przypadek 2: Dwa mobilne i dwa stałe koła pasowe

Rozważmy napięcia i siły, które działają na zbiorze, który składa się z dwóch wsparcia wsparcia A i B z dwoma kół pasowymi.

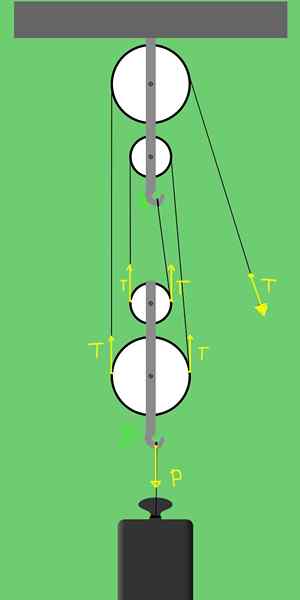Rysunek 3. Siły na platformie 2 stałych kół pasowych i 2 mobilnych koła pasowych.

Wsparcie B ma możliwość poruszania się pionowo, a siły działające na syna:

- Waga P obciążenia, który wskazuje pionowo.

- Dwa napięcia na dużym koładzie koła pasowego i dwa napięcia na małym koło pasowym. W sumie cztery napięcia, wszystkie wskazują.

Aby istniała równowaga translacyjna, konieczne jest, aby siły, które wskazują pionowo w górę równe obciążeniu, które wskazuje. Oznacza to, że należy to spełnić:

T + t + t + t = p

To znaczy, 4 t = p

Z miejsca, w którym wynika z tego, że przyłożona siła t na wolnym końcu liny to zaledwie jedna czwarta wagi z powodu obciążenia, które chce wznieść się., T = p / 4.

Z tą wartością dla napięcia t obciążenie można utrzymywać statyczne lub rosnące ze stałą prędkością. Jeśli zastosowano większe napięcie niż ta wartość, obciążenie przyspieszyłoby, warunek niezbędny do usunięcia go z pozostałej.

Przypadek ogólny: N Mobilne koła pasowe i n stałe koła pasowe

Jak widać w poprzednich przypadkach, dla każdego koła pasowego zestawu mobilnego jest kilka sił w górę przez linę, która przechodzi przez koło pasowe. Ale ta siła nie może być niczym innym niż napięcie nakładane na linę na wolnym końcu.

Tak więc dla każdego koła pasowego mobilnego będzie siła w górę, która jest warta 2T. Ale ponieważ w zestawie mobilnym są n koła pasowe, konieczne jest wówczas wskazanie pionowo w górę:

Może ci służyć: silnik klatki wiewiórki

2 n t

W przypadku równowagi pionowej konieczne jest:

2 n t = p

Dlatego siła nałożona na wolnym końcu to:

T = p / (2 n)

W takim przypadku można powiedzieć, że siła wywierana t mnoży 2 razy na obciążeniu.

Na przykład, gdybyśmy mieli platformę czynnikową 3 stałych koła pasowych i 3 telefony komórkowe, liczba n byłaby równa 3. Z drugiej strony, gdyby obciążenie p = 120 kg, wówczas siła przyłożona na wolnym końcu wynosiłaby t = 120 kg / (2*3) = 20 kg.

Rozwiązane ćwiczenia

Ćwiczenie 1

Rozważ platformę czynnikową złożoną z dwóch stałych kół pasowych i dwóch mobilnych koła pasowych. Maksymalne napięcie, które może obsługiwać linę, wynosi 60 kg. Określ, jakie jest maksymalne obciążenie, które można umieścić.

Rozwiązanie

Gdy obciążenie jest w spoczynku lub ciągle porusza się po jego ciężar P, jest ono związane z napięciem t zastosowanym w linie za pomocą następującej relacji:

P = 2 n t

Ponieważ jest to platforma o dwóch mobilnych i dwóch stałych koła pasowych, a następnie n = 2.

Maksymalne obciążenie, które można umieścić, jest uzyskiwane, gdy t ma maksymalną możliwą wartość, która w tym przypadku wynosi 60 kg.

Maksymalne obciążenie = 2*2*60 kg = 240 kg

Ćwiczenie 2

Znajdź związek między napięciem liny a ciężarem obciążenia, w platformie czynnikowej dwóch kół pasowych, w którym obciążenie przyspiesza przyspieszenie.

Rozwiązanie

Różnica w tym przykładzie w odniesieniu do tego, co widziano do tej pory, należy wziąć pod uwagę dynamikę systemu. Proponujemy więc drugie prawo Newtona w celu znalezienia żądanego związku.

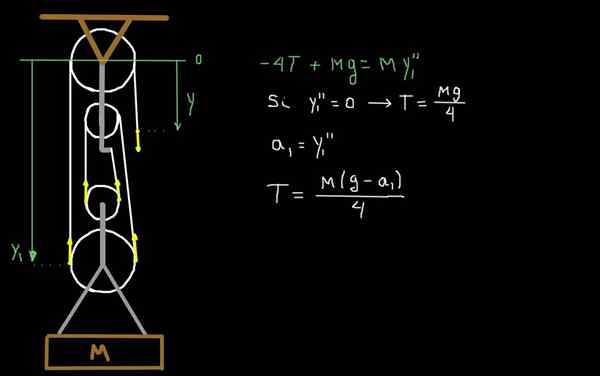Rysunek 4. Dynamika platformy czynnikowej.

Na rycinie 4 rysujemy siły z powodu napięcia T liny. Mobilna część platformy ma całkowitą masę m. Używamy jako system odniesienia na poziomie pierwszego stałego i dodatniego koła pasowego w dół.

Y1 jest najniższą pozycją osi koła pasowego.

Stosujemy drugie prawo Newtona, aby określić przyspieszenie A1 mobilnej części platformy:

Może ci służyć: Twierdzenie Varignon

-4 t + mg = m a1

Ponieważ ciężar obciążenia wynosi p = mg, gdzie g jest przyspieszeniem grawitacji, poprzedni związek można zapisać:

-4T + P = P (A1 / G)

Gdybyśmy chcieli ustalić napięcie stosowane w linie, gdy pewne obciążenie masy jest przyspieszane za pomocą przyspieszenia A1, poprzednia relacja byłaby taka:

T = p (1 - a1 / g) / 4

Zauważ, że jeśli system był w spoczynku lub ciągle poruszał się, to A1 = 0, i odzyskaliśmy to samo wyrażenie, które otrzymaliśmy w przypadku 2.

Ćwiczenie 3

W tym przykładzie stosuje się ten sam zestaw ćwiczeń 1, z tą samą liną, która obsługuje maksymalnie 60 kg napięcia. Pewne obciążenie wzrasta, przyspieszając je od odpoczynku do 1 m/s o 0,5 s, przy użyciu maksymalnego napięcia liny. Znajdź maksymalną masę obciążenia.

Rozwiązanie

Użyjemy wyrażeń uzyskanych w ćwiczeniu 2 i systemie odniesienia na rycinie 4, na którym dodatni adres jest pionowy.

Przyspieszenie obciążenia wynosi a1 = (-1 m/s -0 m/s)/0,5 s = -2 m/s^2.

Waga obciążenia w sile kilogramu jest podana przez

P = 4 t / (1 - a1 / g)

P = 4*60 kg / (1 + 2/9.8) = 199,3 kg

Jest to maksymalna możliwa waga obciążenia bez złamania liny. Należy zauważyć, że uzyskana wartość jest mniejsza niż wartość uzyskana w przykładzie 1, w którym obciążenie przypuszczano z zerowym przyspieszeniem, to znaczy przy spoczynku lub stałej prędkości.

Bibliografia

1. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1. 101-120.
2. Resnick, r. (1999). Fizyczny. Tom. 1. 3 ra ed. po hiszpańsku. Continental Editorial Company S.DO. c.V. 87-103.
3. Giancoli, zm. 2006. Fizyka: zasady z aplikacjami. 6th. Wyd. Prentice Hall. 72 - 96.
4. Hewitt, Paul. 2012. Konceptualna nauka fizyczna. 5. Wyd. osoba.38-61.
5. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wyd. Cengage Learning. 100 - 119.