Charakterystyka amplitudy falowej, wzory i ćwiczenia

Amplituda fal Jest to maksymalne przemieszczenie doświadczane przez punkt w fali w odniesieniu do pozycji równowagi. Fale objawiają wszędzie i na wiele sposobów na otaczającym nas świecie: w oceanie, w dźwięku i w linie instrumentu, który go wytwarza, w świetle, na powierzchni Ziemi i wiele więcej.

Jednym ze sposobów wytwarzania fal i badania ich zachowania jest obserwowanie wibracji liny, która ma ustalony koniec. Wykonując zakłócenie na drugim końcu, każda cząstka linii oscyluje, a wraz z nią energia zakłóceń jest przenoszona w postaci sukcesji pulsów w całym.

Fale objawiają na wiele sposobów w naturze. Źródło: Pixabay.

Gdy energia się rozprzestrzenia, lina, która ma być doskonale elastyczna, przyjmuje typową formę sinusoidalną z grzbietami i dolinami pokazanymi na rysunku, która pojawia się poniżej w poniższej sekcji.

[TOC]

Charakterystyka i znaczenie amplitudy falowej

Amplituda A jest odległością między szczytem a osą odniesienia lub poziomem 0. Jeśli jest preferowany, między doliną a osą odniesienia. Jeśli zakłócenia w linie jest łagodne, amplituda A jest niewielka. Jeśli wręcz przeciwnie, zakłócenia jest intensywne, amplituda będzie większa.

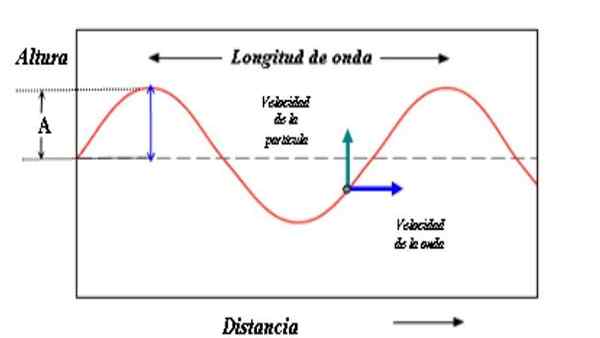Model opisujący falę składa się z krzywej sinusoidalnej. Amplituda fali to odległość między grzebieniem lub doliną a osą odniesienia. Źródło: PACO [CC BY-SA 3.0 (http: // creativeCommons.Org/licencje/by-sa/3.0/]]

Wartość amplitudy jest również miarą energii, która zużywa falę. Intuicyjne jest to, że wielka amplituda jest związana z większą energią.

W rzeczywistości energia jest proporcjonalna do kwadratu amplitudy, która wyrażała matematycznie, jest:

I ∝a²

Może ci służyć: wzajemna indukcyjność: wzór/współczynnik, zastosowania, ćwiczenia

Gdzie ja jest intensywnością fali, z kolei związaną z energią.

Rodzaj fali wytwarzanej w przykładowej linie należy do kategorii fal mechanicznych. Ważną cechą jest to, że każda cząstka na linie zawsze pozostaje bardzo blisko jej pozycji równowagi.

Cząstki nie poruszają się ani nie poruszają przez linę. Zakładają się w górę i w dół. Jest to wskazane w górnym schemacie z zieloną strzałą, jednak fala wraz z energią, podróżuje od lewej do prawej (niebieska strzałka).

Fale rozprzestrzeniające się w wodzie dostarczają niezbędnych dowodów, aby się o tym przekonać. Obserwowanie ruchu arkusza, który wpadł w staw, widać, że po prostu oscyluje ruch wody. Nie idzie bardzo daleko, przynajmniej jasne, że istnieją inne siły, które zapewniają inne ruchy.

Model fali pokazany na rysunku składa się z powtarzającego się wzoru, w którym odległość między dwoma grzbietami jest długość fali λ. Jeśli chcesz, długość fali oddziela również dwa identyczne punkty od fali, nawet jeśli nie są one na szczycie.

Matematyczny opis fali

Oczywiście falę można opisać funkcją matematyczną. Funkcje okresowe, takie jak zatokę i cosinus, są idealne do zadania, niezależnie od tego, czy chcesz reprezentować falę zarówno w przestrzeni, jak i w czasie.

Jeśli nazywamy oś pionową na rysunku i osi poziomej, nazywamy to „t”, wówczas zachowanie fali w czasie wyraża się przez:

y = a cos (ωt + δ)

W przypadku tego idealnego ruchu każda cząstka liny oscyluje prostym ruchem harmonicznym, który powstaje dzięki sile bezpośrednio proporcjonalnej do przemieszczenia wykonanego przez cząstkę.

Może ci służyć: Model atomowy Dirac Jordan: Charakterystyka i postulaty

W proponowanym równaniu A, ω i δ są parametrami opisującymi ruch, będąc do amplituda Wcześniej zdefiniowane jako maksymalne przesunięcie doświadczone przez cząstkę w odniesieniu do osi odniesienia.

Argument cosinus jest nazywany Faza ruchu I δ jest stała fazowa, Jaka jest faza, gdy t = 0. Zarówno funkcja cosinus, jak i funkcja sinusoidalna są odpowiednie do opisania fali, ponieważ różnią się tylko od siebie π/2.

Zwykle możliwe jest wybór t = 0 z δ = 0, aby uprościć wyrażenie, uzyskując:

y = a cos (ωt)

Kiedy ruch jest powtarzalny zarówno w przestrzeni, jak i czasie, istnieje charakterystyczny czas koniec dyskusji, zdefiniowane jako czas potrzebny na wykonanie cząstki do pełnej oscylacji.

Opis fali w czasie: parametry charakterystyczne

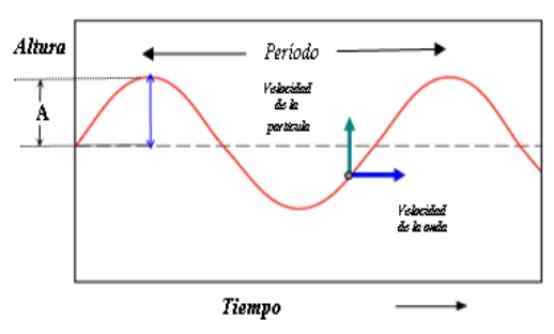Ten rysunek pokazuje opis fali w czasie. Odległość między grzbietami (lub dolinami) odpowiada teraz okresowi fali. Źródło: PACO [CC BY-SA 3.0 (http: // creativeCommons.Org/licencje/by-sa/3.0/]]

Teraz zarówno piersi, jak i cosinus powtarzają swoją wartość, gdy faza wzrasta w wartości 2π, tak:

ωt = 2π → ω = 2π /t

Ω jest nazywane Kątowa częstotliwość ruchu I ma wymiary odwrotności czasu, będąc jego jednostkami w systemie międzynarodowym Radio / drugim lub drugim^-1.

Wreszcie możesz zdefiniować Częstotliwość ruchu F, jako odwrotnie lub wzajemne okres. Reprezentuje liczbę grzbietów na jednostkę czasu, w którym to przypadku:

F = 1/t

Ω = 2πf

Zarówno F, jak i ω mają te same wymiary i jednostki. Oprócz drugiego^-1, który nazywa się Hertz lub Hertzio, powszechne jest o tym Rewolucje na sekundę albo obroty na minutę.

Prędkość fali v, które należy podkreślić, że nie jest to takie samo jak ten doświadczony przez cząstki, można go łatwo obliczyć, jeśli znane są długość fali λ i częstotliwość F:

Może ci służyć: ciała świetliste: cechy i sposób, w jaki generują własne światło

V = λf

Jeśli oscylacja doświadczana przez cząstki ma prosty typ harmoniczny, częstotliwość kątowa i częstotliwość zależą tylko od natury cząstek oscylacyjnych i charakterystyk układu. Amplituda fali nie wpływa na te parametry.

Na przykład, grając nutę muzyczną na gitarze, nuta zawsze będzie miała ten sam ton, chociaż jest dotykana większą lub mniejszą intensywnością, w ten sposób zawsze będzie brzmiało jak a, chociaż jest słychać silniejszy lub bardziej miękki w kompozycja, na fortepianie lub na gitarze.

W naturze fale transportowane w środowisku materialnym we wszystkich kierunkach są osłabione, ponieważ energia rozprasza. Z tego powodu amplituda maleje wraz z odwrotnością odległości R do źródła, możliwe potwierdzenie tego:

A∝1/r

Ćwiczenie rozwiązane

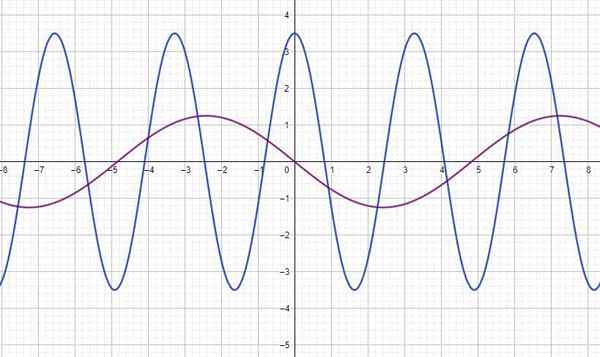
Rysunek pokazuje funkcję y (t) dla dwóch fal, gdzie I jest w metrach i T w sekundy. Dla każdego znajduje się:

a) amplituda

b) Okres

c) Częstotliwość

d) Równanie każdej fali pod względem piersi lub konsenos.

Odpowiedzi

a) Jest mierzony bezpośrednio z wykresu, z pomocą siatki: fala niebieska: a = 3.5m; Fuchsia fala: a = 1.25 m

b) Odczytuje również wykres, określając oddzielenie dwóch pików lub dolin, kolejnych: fala niebieska: t = 3.3 sekundy; Fuchsia fala t = 9.7 sekund

c) Oblicza się, pamiętając, że częstotliwość jest wzajemną okresu: fala niebieska: f = 0.302 Hz; Fuchsia Wave: F = 0.103 Hz.

d) Niebieska fala: y (t) = 3.5 cos (ωt) = 3.5 cos (2πf.t) = 3.5 cos (1.9t) m; Fuchsia fala: y (t) = 1.25 grzech (0.65t) = 1.25 cos (0.65t+1.57)

Należy zauważyć, że fala Fuchsia jest przestarzała π/2 w odniesieniu do niebieskiego, możliwe przedstawienie jej z funkcją sinusoidalną. Lub przesunięte cosinus π/2.