Fizyczny

Definicja przyspieszenia dośrodkowego, formuły, obliczenia, ćwiczenia

Definicja przyspieszenia dośrodkowego, formuły, obliczenia, ćwiczenia

przyspieszenie dośrodkowe DoC, Nazywany również promieniowaniem lub normalnym, to przyspieszenie przenosi obiekt mobilny podczas opisywania okrągłej trajektorii. Jego wielkość jest v2/R, Gdzie R Jest to promień koła, jest on skierowany w kierunku jego środka i jest odpowiedzialny za telefon komórkowy, aby pozostać na swojej trasie.

Wymiary przyspieszenia dośrodkowego wynoszą długość na jednostkę. W systemie międzynarodowym są M/s2. Jeśli z jakiegoś powodu przyspieszenie dośrodkowe znika, również siła, która zmusza telefon komórkowy do utrzymania okrągłej trajektorii.

Obiekty obrotowe mają przyspieszenie dośrodkowe, które jest skierowane w kierunku centrum trajektorii. Źródło: Pixabay

Tak dzieje się z samochodem, który próbuje podać krzywą na płaskim i mrozowym torze, w którym tarcie między podłogą a kółkami jest niewystarczające, aby samochód przejął krzywą. Dlatego jedyną możliwością, którą pozostawiłeś, jest poruszanie się w linii prostej i dlatego wychodzisz z krzywej.

[TOC]

Ruchy okrągłe

Gdy obiekt porusza się w okręgu, przez cały czas przyspieszenie dośrodkowe jest promieniowo skierowane w kierunku środka obwodu, kierunek prostopadły do ​​trajektorii następuje.

Ponieważ prędkość jest zawsze styczna do trajektorii, więc prędkość i przyspieszenie dośrodkowe okazują się prostopadłe. Dlatego prędkość i przyspieszenie nie zawsze mają ten sam kierunek.

W tych okolicznościach telefon komórkowy ma możliwość opisania obwodu ze stałą lub zmienną prędkością. Pierwszy przypadek jest znany jako ruch okrągły jednolity lub MCU przez akronim, drugim przypadkiem będzie zmienny ruch okrągły.

Może ci służyć: co to jest wycieranie emisji? (Z przykładami)

W obu przypadkach przyspieszenie dośrodkowe jest odpowiedzialne za utrzymanie krążenia mobilnego, zajmując, że prędkość zmienia się tylko w kierunku i kierunku.

Jednak, aby mieć zmienny ruch kołowy, konieczne byłby inny element przyspieszenia w tym samym kierunku prędkości, który jest odpowiedzialny za zwiększenie lub zmniejszenie prędkości. Ten komponent przyspieszenia jest znany jako Styczne przyspieszenie.

Zmienny ruch okrągły i ruch krzywiniowy mają oba elementy przyspieszenia, ponieważ ruch krzywiakowy może sobie wyobrazić jako trasa przez niezliczone łuki o obwodzie, które tworzą zakrzywioną trajektorię.

Siła dośrodkowa

Teraz siła jest odpowiedzialna za zapewnienie przyspieszenia. Dla satelity, który krąży po ziemi, to siła grawitacji. A ponieważ grawitacja zawsze działa prostopadle do trajektorii, nie zmienia prędkości satelity.

W tym przypadku grawitacja działa jak siła dośrodkowa, że nie jest to klasa specjalna ani oprócz siły, ale taka, która w przypadku satelity jest promieniowo skierowana w kierunku środka ziemi.

W innych rodzajach ruchu okrągłego, na przykład samochodu, który wymaga krzywej, rola siły dośrodkowej jest interpretowana przez siłę statyczną, która zmusza telefon komórkowy do obracania.

Wzory dla przyspieszenia dośrodkowego

Przyspieszenie dośrodkowe jest obliczane na podstawie wyrażenia:

AC = v2/R

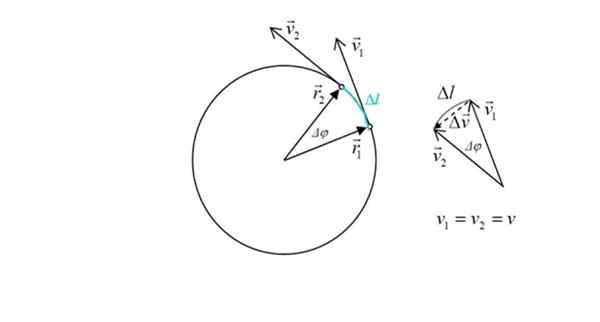Schemat obliczania przyspieszenia dośrodkowego w telefonie komórkowym z MCU. Źródło: Źródło: Ilevanat [CC BY-SA 3.0 (https: // creativeCommons.Org/licencje/by-sa/3.0)]

To wyrażenie zostanie wydedukowane poniżej. Z definicji przyspieszenie to zmienność prędkości w czasie:

Może ci służyć: źródła światła: typy i urządzenia, które emitują światło

Górny schemat pokazuje na lewej figurze, dwa punkty, przez które przechodzi mobil R w sensie przeciwhorarium. Zauważ, że wielkość prędkości jest taka sama w obu przypadkach, ale nie kierunek lub znaczenie.

Telefon komórkowy używa czasu δT Na trasie, która jest niewielka, ponieważ punkty są bardzo blisko.

Rysunek pokazuje również dwa wektory pozycji R1 I R2, którego moduł jest taki sam: radio R obwodu. Kąt między obiema punktami wynosi φφ. W kolorze zielonym ukłon Wycieczka po telefonie komórkowym, oznaczonym jako ΔL.

Na rysunku po prawej stronie widać, że wielkość δv, Zmiana prędkości jest w przybliżeniu proporcjonalna na ΔL, ponieważ kąt φφ jest mały. Ale zmiana prędkości jest powiązana dokładnie z przyspieszeniem. Trójkąt jest ostrzeżony przez sumę wektorów, że:

v1 + Δv = v2 → δv = v2 - v1

Δv To interesujące, ponieważ jest proporcjonalne do przyspieszenia dośrodkowego. Na podstawie figury ostrzega, że ​​będąc małym kątem φφ, wektor δv Jest w prostopadłej esencji oba v1 tak jak v2 i wskazuje na środek obwodu.

Chociaż wektory wyróżniają się odważne, pod względem skutków natury geometrycznej, pracujemy z modułami lub wielkościami tych wektorów, niezależnie od zapisu wektora.

Coś innego: musisz użyć definicji kąta centralnego, czyli:

Δφ= ΔL/r

Teraz obie liczby są porównywane, które są proporcjonalne od kąt δφ To jest powszechne:

Może ci służyć: co to jest spolaryzowane światło?

 

Dzielenie między δT:

 Ponieważ z definicji prędkości wynosi v = δL/ δt. Ale δV/ ΔT Właśnie to wielkość przyspieszenia dośrodkowego, o co chodzi. W ten sposób osiągnięto wyrażenie opisane na początku:

DoC= v2/R

Ćwiczenie rozwiązane

Cząstka porusza się w okręgu 2.Radio 70 m. W pewnym momencie jego przyspieszenie wynosi 1.05 m/s2 W kierunku, który wykonuje kąt 32.0º z dyrekcją ruchu. Oblicz swoją prędkość:

a) W tym czasie

b) 2.00 sekundy później, zakładając stałe przyspieszenie styczne.

Odpowiedź

Jest to zróżnicowany ruch okrągły, ponieważ stwierdzenie wskazuje, że przyspieszenie ma dany kąt z kierunkiem ruchu, który nie jest lub 0º (nie mógłby to być ruch kołowy) lub 90º (byłby to jednolity ruch kołowy).

Dlatego dwa składniki - promieniowe i styczne - współistnica. Zostanie oznaczony jakoC jużT i pojawiają się na poniższym rysunku. Zielony wektor to wektor przyspieszenia netto lub po prostu przyspieszenie Do.

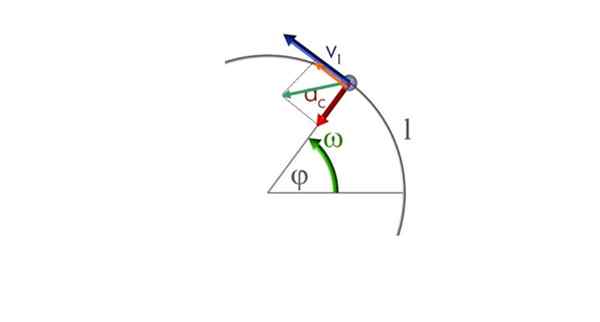Cząstka porusza się w okrągłej trajektorii w sensie przeciwhordowym i różnorodnym ruchu okrągłym. Źródło: Commons.Wikimedia.org

a) Obliczenie komponentów przyspieszenia

DoC = a.cos θ = 1.05 m/s2 . cos 32.0º = 0.89 m/s2 (w czerwonym)

DoT = a.sin θ = 1.05 m/s2 . Sen 32.0º = 0.57 m/s2 (w Orange)

Obliczanie prędkości mobilnej

PonieważC = v2/R, Więc:
b) 2 sekundy później prędkość v zostanie zwiększony dzięki styczniowej komponencie przyspieszenia

v = valbo +DoT. T = 1.6 m/s + (0.57 x 2) m/s = 2.74 m/s

Bibliografia

  1. Giancoli, zm. Fizyka. 2006. Zasady z aplikacjami. Szósta edycja. Prentice Hall. 107-108.
  2. Hewitt, Paul. 2012. Konceptualna nauka fizyczna. PIĄTA EDYCJA.osoba.106 - 108.