Absorbancja, co jest, przykłady i ćwiczenia

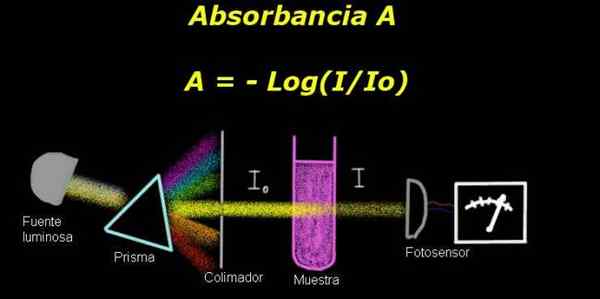
Absorbancja Jest to logarytm z ujemnym znakiem ilorazu między wschodzącą intensywnością światła a intensywnością padania światła na próbce półprzezroczystego roztworu, który został oświetlony światłem monochromatycznym. Ten iloraz jest transmitancja.

Nazywa się fizyczny proces przejścia światła przez próbkę Lumowinous Transmission, A absorbancja jest jej miarą. Stąd absorbancja staje się najmniejszym logarytmem transmitancji i jest ważnym faktem do określenia stężenia próbki, która jest ogólnie rozpuszczona w rozpuszczalniku, takim jak woda, alkohol lub inna inna.

Rysunek 1. Schemat procesu absorbancji. Przygotowane przez f. Zapata

Aby zmierzyć absorbancję, wymagane jest urządzenie Electro-fotometr, z którym mierzony jest prąd, który jest proporcjonalny do incydentu z świetlistą intensywnością.

Podczas obliczania transmitancji sygnał intensywności odpowiadający samemu rozpuszczalnikowi jest ogólnie mierzony Io.

Następnie umieszczono próbkę rozpuszczoną w rozpuszczalniku z tymi samymi warunkami oświetlenia. Miara mierzona za pomocą elektrootometru jest oznaczona jako Siema, co pozwala obliczyć transmitancję T Zgodnie z następującym formułem:

T = i / ialbo

Jest to ilość uwolniona. Absorbancja a Jest to wyrażone jako:

A = - log (t) = - log (i / ialbo)

[TOC]

Absorbancja molowa i pochłanianie

Cząsteczki, które składają się na chemikalia, są w stanie wchłonąć światło, a miarą tego jest dokładnie absorbancja. Jest wynikiem interakcji między fotonami i elektronami molekularnymi.

Dlatego jest to wielkość, która będzie zależeć od gęstości lub stężenia cząsteczek, które tworzą próbkę, a także od ścieżki optycznej lub odległości przebywającej przez światło. 

Możesz Ci służyć: trzecie prawo Newtona: aplikacje, eksperymenty i ćwiczenia

Dane eksperymentalne wskazują, że absorbancja DO jest liniowo proporcjonalny do stężenia C i odległość D Światło podróżowało. Aby obliczyć go na podstawie tych parametrów, można ustalić następujący wzór:

A = ε⋅C⋅D

W poprzednim formule, ε Jest to stała proporcjonalności znana pod nazwą Absorbowanie molowe.

Absorbracja molowa zależy od rodzaju substancji i długości fali, z którą mierzona jest absorbancja. Absorbowanie molowe Jest również wrażliwy na temperaturę próbki i pH tego samego.

Prawo piwa-lambert

Ten związek między absorbancją, pochłanianiem, stężeniem i odległością od grubości ścieżki, którą światło podąża w próbce, jest znana jako prawo piwa-lambert.

Rysunek 2. Prawo piwa - Lambert. Źródło: f. Zapata,

Poniżej znajduje się kilka przykładów tego, jak z niego korzystać.

Przykłady

Przykład 1

Podczas eksperymentu próbka z czerwonym światłem lamp laserowych helu, których długość fali wynosi 633 nm. Elektro-fotometr mierzy 30 mV, gdy światło laserowe wpływa bezpośrednio na 10 mV, gdy przechodzi przez próbkę. 

W takim przypadku przekazanie wynosi:

T = I / IO = 10 mV / 30 mv = ⅓.

A absorbancja to:

A = - log (⅓) = log (3) = 0,48 

Przykład 2

Jeśli ta sama substancja jest umieszczona w pojemniku, który ma połowę grubego.

Należy wziąć pod uwagę, że jeśli grubość spada do połowy, wówczas absorbancja proporcjonalna do grubości optycznej zmniejsza się o połowę, to znaczy A = 0,28. Ton transmitancji będzie podawany przez następującą relację:

Może ci służyć: ujęcie pionowe: wzory, równania, przykłady

T = 10-a = 10^(-0.28) = 0,53

Electro-fotometr zaznaczy 0,53*30 mV = 15,74 mV.

Rozwiązane ćwiczenia

Ćwiczenie 1

Wymagane jest określenie pochłaniania molowego pewnego opatentowanego związku, który jest w roztworze. W tym celu roztwór z światłem z lampy sodowej 589 nm jest oświetlony. Próbka zostanie umieszczona na grubości 1,50 cm.

Opiera się na roztworze stężenia 4,00 × 10^-4 moli na litr, a transmitancja mierzy się, powodując 0,06. Określ za pomocą tych danych Absorbota trzonowa próbki.

Rozwiązanie 

Po pierwsze, określa się absorbancja, która jest definiowana jako najmniej logarytm oparty na dziesięciu transmitancji:

A = - log (t)

A = - log (0,06) = 1,22

Następnie stosuje się prawo Lambert-Beer, które ustanawia związek między absorbancją, pochłanianiem molowym, stężeniem i długością optyczną:

A = ε⋅C⋅D

Oczyszczanie pochłaniania trzonowego Uzyskuje się następujący związek:

ε = a/(c⋅d)

zastąpienie podanych wartości:

ε = 1,22/(4,00 × 10^-4 m⋅1,5 cm) = 2030 (M⋅CM)^-1

Poprzedni wynik został zaokrąglony do trzech znaczących cyfr.

Ćwiczenie 2

Aby poprawić dokładność i określić błąd pomiaru pochłaniania molowego próbki w ćwiczeniu 1, próbka jest sukcesywnie rozcieńczona w połowie stężenia, a transmitancja jest mierzona w każdym przypadku.

Zaczynając od CO = 4 × 10^-4 m z transmitancją t = 0,06 Uzyskuje się następującą sekwencję danych dla transmitancji i absorbancji obliczonej na podstawie transmitancji:

Co/1-> 0,06-> 1,22

Co/2-> 0,25-> 0,60

CO/4-> 0,50-> 0,30

Co/8-> 0,71-> 0,15

Co/16-> 0,83-> 0,08

Co/32-> 0,93-> 0,03

CO/64-> 0,95-> 0,02

Co/128-> 0,98-> 0,01

Co/256-> 0,99-> 0,00

Z tymi danymi zrób:

Może ci służyć: fale stacjonarne: wzory, cechy, typy, przykłady

a) Wykres absorbancji oparty na stężeniu.

b) liniowa regulacja danych i znajdź nachylenie.

c) Z uzyskanego nachylenia oblicz pochłanianie trzonowe.

Rozwiązanie 

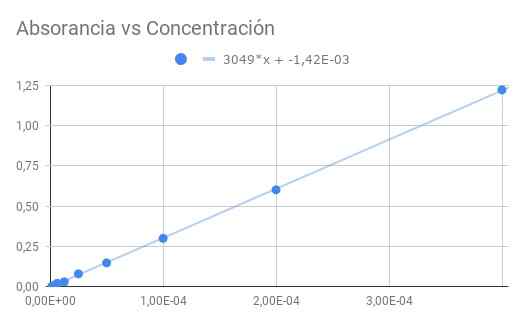Rysunek 3. Absorbancja vs stężenie. Źródło: f. Zapata.

Otrzymane nachylenie jest iloczynem chłonności molowej przez odległość optyczną, więc dzieląc nachylenie przez długość 1,5 cm

ε = 3049/1,50 = 2033 (M⋅CM)^-1

Ćwiczenie 3

Z danymi z ćwiczenia 2: 

a) Oblicz chłonność dla każdego danych. 

b) Określ średnią wartość absorbalności molowej, odchylenie standardowe i błąd statystyczny związany ze średnią.

Rozwiązanie 

Absorbowanie molowe oblicza się dla każdego z testowanych stężeń. Przypomnij sobie, że warunki oświetlenia i odległość optyczna pozostają stałe.

Wyniki dla pochłaniania trzonowego to:

2033, 2007, 2007, 1983, 2158, 1681, 2376, 1 872, 1862 w jednostkach 1/(m*cm).

Z tych wyników możemy przyjąć średnią wartość:

= 1998 (m*cm)^-1

Ze standardowym odchyleniem: 184 (m*cm)^-1

Średni błąd jest odchyleniem standardowym podzielonym przez pierwiastek kwadratowy numeru danych, to znaczy:

Δ = 184/9^0,5 = 60 (m*cm)^-1

Wreszcie stwierdzono, że opatentowana substancja ma molowe pochłanianie przy częstotliwości 589 nm wytwarzanej przez lampę sodową:

= (2000 ± 60) (m*cm)^-1

Bibliografia

1. Atkins, str. 1999. Chemia fizyczna. Omega Editions. 460-462.
2. Przewodnik. Transmitancja i absorbancja. Odzyskane z: chemii.Laguia2000.com
3. Toksykologia środowiskowa. Transmitancja, absorbancja i prawo Lamberta. Odzyskane z: repozytorium.Innovationumh.Jest
4. Fizyka przygodowa. Absorbancja i transmitancja. Odzyskane z: rpfisica.Blogspot.com
5. Sistofotometria. Odzyskane z: chem.Librettexts.org
6. Toksykologia środowiskowa. Transmitancja, absorbancja i prawo Lamberta. Odzyskane z: repozytorium.Innovationumh.Jest
7. Wikipedia. Absorbancja. Odzyskane z: Wikipedia.com
8. Wikipedia. Spektrofotometria. Odzyskane z: Wikipedia.com