Tom

Wyjaśniamy, jaka jest objętość, jej wzory, jednostki, jak ją obliczyć i podawać kilka przykładów

Jaki jest tom?

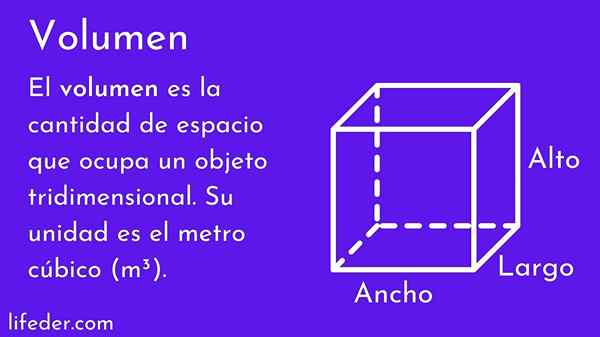
On tom ciała to wartość liczbowa, która mierzy ilość miejsca zajmowanego przez nią. Im wysoka, szerokość i głębokość determinują objętość, tym większa, tym większa zajęta przestrzeń.

Koncepcja objętości ma ogromne znaczenie, ponieważ świat jest trzy -wymiar i wszystkie obiekty mają szerokość, wysokość i głębokość, dlatego mają objętość. Ludzie często go używają, na przykład, szacując, czy meble, które chcą kupić, pasuje do ich pokoju, czy też wprowadzają określoną rozmiar sukienki.

W niektórych obszarach nauki i inżynierii, na przykład podczas pracy z płynami, czy to płynami, czy gazami, zajęta objętość przybiera ogromne znaczenie: podczas napełniania pojemników i pompowania płynów, takich jak woda lub przy projektowaniu statku dla statku, aby upewnić się Nie tonie. Wszystko to sprawia, że ​​określenie tego dla wielu procesów jest niezbędne.

Istnieją wzory do obliczania objętości ciał geometrycznych w regularnych kształtach, takich jak pryzmaty, kule, cylindry i stożki, na przykład, w zależności od niektórych jej wymiarów. Są też sposoby na znalezienie objętości nieregularnych obiektów, co zostanie opisane nieco później.

Wzory objętości w postaci geometrycznych

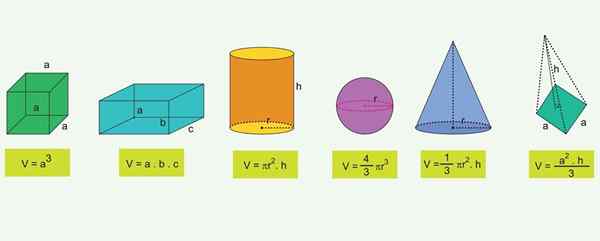Lista najczęstszych liczb geometrycznych i wzór ich objętości

W przypadku najbardziej znanych obiektów geometrycznych istnieją wzory, które pozwalają obliczyć jego objętość:

• Sześcian

V = ℓ³ 

Gdzie v reprezentuje objętość, a ℓ jest krawędzią (stroną) kostki.

• Równoległościan

Równoległobok to prostokątny pudełko o szerokości „A”, długiej ℓ i wysokości „H”. Jego objętość jest dana przez iloczyn trzech wymiarów:

V = a ∙ ℓ ∙ h

• Kula

Objętość kuli zależy od jej promienia r:

Może ci służyć: Nicolás Copernico

• Prosty okrągły cylinder

Objętość prostego okrągłego cylindra to produkt między obszarem jego podstawy a jego wysokością „h”. Ponieważ podstawa to album radiowy „R”, którego obszar jest a = π · r², Tom pozostaje:

V = πr²∙ h

• Kiciuś

Objętość stożka jest jedną trzecią produktu między obszarem okrągłej podstawy A i wysokością. Jak a = πr², Więc:

• Piramida

Dla piramidy, której obszar podstawowy jest a i ma wysokość „h”, objętość jest podana przez:

Jeśli piramida ma kwadratową podstawę z boku „A”, jak na rysunku, podstawa podstawy jest to² A objętość piramidy to:

V = (1/3) ⋅A²⋅h

• Pryzmat

Objętość pryzmatu jest produktem między obszarem podstawy A i wysokością „H”:

V = a ∙ h

Jednostki głośności

W międzynarodowym systemie jednostek jednostką do objętości jest miernik sześcienny lub m³, podczas gdy w systemie anglo -saksonu jest to stopa sześcienna lub ft³ (z Stopy, który w języku angielskim oznacza „stopę”).

Istnieje wiele innych jednostek, zgodnie z wielkością zajętej przestrzeni. Na przykład kilometry sześcienne km³ Dla większych woluminów lub milimetrów sześciennych mm³ Dla małych tomów. Istnieją również lokalne jednostki użytkowania.

Należy również wspomnieć o jednostkach pojemności, ściśle związanych z objętościami, które są najlepiej stosowane w przypadku cieczy. Centralną jednostką pojemności jest litr, skrócony L, który jest równoważny DM³ (Decimetr sześcienny).

Inne jednostki, o których warto wspomnieć, to galon, cal sześcienny, kubek i dna moczanowa, te ostatnie używane do dawkowania leków.

Może ci służyć: metoda porównawcza

Jak mierzy się objętość?

Objętość ciała, jak każda inna miara, jest przeprowadzana w porównaniu z odpowiednim wzorem, w tym przypadku jednostka objętości.

Jednostka objętościowa jest zdefiniowana jako sześcian, którego krawędź mierzy 1 jednostkę. Ta jednostka może być miernik, centymetr, stopa, cal lub dowolne inne. Następnie objętość obiektu odpowiada ilości jednostek sześciennych zajmowanych przez figurę i jest zawsze ilością dodatnią.

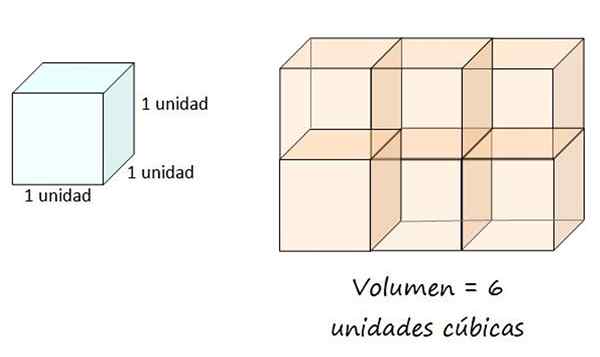Jednostka sześcienna jest zdefiniowana jako objętość wiadra z krawędzią równą 1, więc pudełko po prawej stronie ma objętość 6 jednostek sześciennych. Źródło: f. Zapata.

Objętość ciała geometrycznego

Jeśli chodzi o korpus geometryczny, jak już wspomniano, objętość jest obliczana przez odpowiedni wzór, mierząc wymiary wskazane przez formułę.

Na przykład, jeśli chcesz poznać objętość kuli, konieczne jest zmierzenie jej średnicy, a wraz z nią jego promień jest znany, czyli w połowie. Jeśli jest to prostokątny pudełko, mierzona jest szerokość, wysokość i głębokość tego samego.

Następnie wartości wymagane w formule są wstawiane, uważając, aby wszystkie jednostki były takie same, wymagane operacje są przeprowadzane, istnieje objętość obiektu.

Objętość nieregularnego ciała

Nieregularne substancje stałe nie mają geometrycznego kształtu, takiego jak kamień lub mrugnięcie. Mimo to można znaleźć jego objętość za pomocą stopniowanego pojemnika pełnego wody, za pomocą metody przemieszczenia cieczy.

Po pierwsze, objętość zajmowana przez wodę jest określana, a następnie nieregularny obiekt jest całkowicie zanurzony, mierząc nową objętość, która jest większa niż oryginał. Objętość nieregularnego obiektu jest różnicą między tą objętością a samą wody.

Może ci służyć: Genie Wiley, dzika dziewczyna, która rozpoznała tylko jej imię

Aby ta metoda działała, obiekt nie powinien być wykonany z żadnej substancji, która jest łatwo rozpuszczona w wodzie, musi pozostać całkowicie zanurzona i oczywiście musisz mieć ukończony pojemnik o niezbędnym rozmiarze, aby całkowicie pomieścić go.

Przykłady objętości

Przybliżona objętość niektórych znanych obiektów to:

• Ziemia: 1.08321 × 10¹² km³
• Amazonas River: 225.000 m³/s (objętość na jednostkę czasu nazywa się „przepływem”)
• Wielka piramida Giza: 2.600.000 m³
• Piłka nożna: 5600 cm³
• Plecak: 50 dm³

Objętość i masa

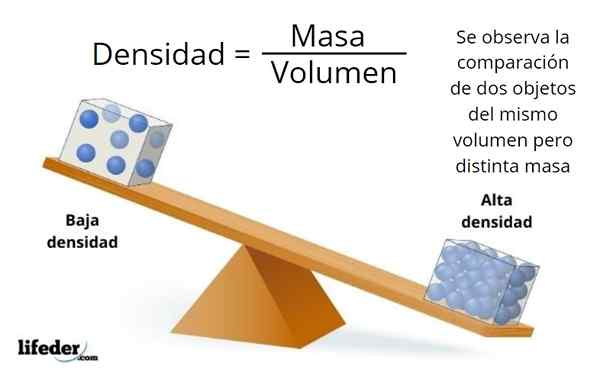
Objętość i masa nie są synonimami, pierwszy jest powiązany z wymiarami obiektu, a drugi z ilością zawieranej przez niego materii.

Może być dużo materii w obiekcie małych wymiarów lub bardzo niewiele w dużym obiekcie, który zależy od gęstości materiału, który jest stosunkiem między masą a objętością obiektu:

Rozwiązane ćwiczenia

Ćwiczenie 1

Oblicz objętość prostokątnego pudełka, którego wymiary wynosi 34 cm × 22 cm × 8 cm.

• Rozwiązanie

Objętość prostokątnego pudełka jest po prostu produktem jego trzech wymiarów:

V = 34 cm × 22 cm × 8 cm = 5984 cm³

Ćwiczenie 2

Podstawa czworokątnej piramidy ma powierzchnię 16 cm² A jego wysokość wynosi 6 cm. Oblicz objętość wspomnianej piramidy.

• Rozwiązanie

Wzór podany powyżej dla objętości piramidy jest używany, znany obszar jej podstawy:

A wartości numeryczne są zastąpione:

V = (1/3) × 16 cm² × 6 cm = 32 cm³