Charakterystyczne wektory jednostkowe, jak to wydostać, przykłady

Wektory jednostkowe to te, których moduł, wielkość lub rozmiar są równe wartości numerycznej. Wektory jednostkowe są przydatne do wskazania kierunku innych wektorów innych niż jednostki.

Przypomnij sobie, że wektory to byty matematyczne, które matematycznie reprezentują wielkości fizyczne, które zależą od kierunku, takie jak siła, prędkość, przyspieszenie i inne.

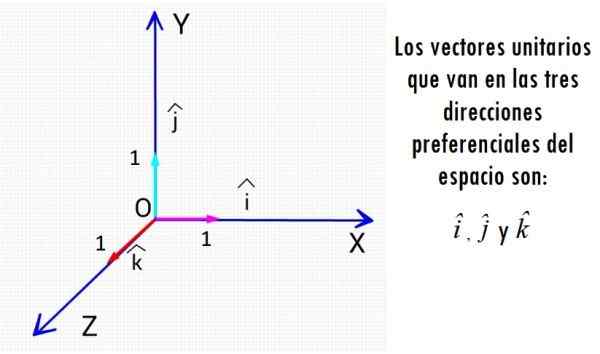
Najbardziej znane wektory jednostkowe to trzy wektory, które idą w kierunku osi kartezjańskich. Źródło: f. Zapata.

Niezależnie od powiązanej wielkości fizycznej, wektory jednostkowe są istotami pozbawionymi jednostek miary, a ich wielkość jest zawsze 1, czysta liczba.

Na przykład prędkość cząstki, która porusza się z prędkością 3 m/s i idzie w kierunku dodatnim kierunku osi karteńskiej x: v = (3 m/s) Siema, gdzie odważna litera jest używana do oznaczenia kwot wektora. W tym przykładzie moduł v To 3 m/s i moduł wektora jednostki Siema jest 1 (bez jednostek).

[TOC]

Moduł, kierunek i znaczenie

Biorąc pod uwagę ważne. W momencie reprezentowania kwoty wektora konieczne jest jasne wskazanie tych aspektów.

Teraz wektor jednostkowy może mieć dowolny kierunek i preferowane znaczenie, ale wielkość musi być zawsze równa 1.

Wektory jednostkowe są używane do wskazania prywatnego adresu w przestrzeni lub w płaszczyźnie. Jeśli na przykład musimy pracować ze wszystkimi siłami działającymi wzdłuż osi poziomej, ponieważ wektor jednostkowy w tym kierunku pomaga nam odróżnić te siły od innych skierowanych w innym kierunku.

I aby odróżnić je od wektorów innych niż jednostki, Bold jest zwykle używany w druku i umieszcza na przykład akcent obwodowy, na przykład:

Może ci służyć: stacjonarna teoria stanu: historia, wyjaśnienie, wiadomości

W przypadku odręcznych tekstów wystarczy umieścić Circlejo, aby zrozumieć, że jest to wektor jednostkowy.

Charakterystyka wektora jednostkowego

Matematycznie wektor jednostkowy:

Jest to element, który należy do przestrzeni wektorowej ℛ wymiaru n, taka |v|. = 1, gdzie słupki oznaczają „moduł”.

Możemy to ustalić:

-Jednostki moduł wektorowy to zawsze 1, nie ma znaczenia, czy jest to siła, prędkość czy inny wektor.

-Wektory jednostkowe mają określony kierunek, a także kierunek, taki jak wektor jednostki w kierunku pionowym, co może mieć sens w górę lub w dół.

-Wektory jednostkowe mają punkt pochodzenia. Gdy jest reprezentowany przez kartezjański układ współrzędnych, powiedział punkt z pochodzeniem układu: (0,0) Jeśli jest to płaszczyzna lub (0,0,0), jeśli wektor znajduje się w trójwymiarowej przestrzeni.

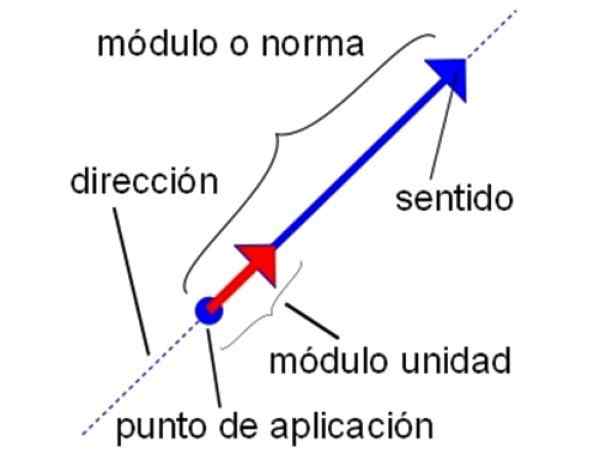Charakterystyka wektora jednostki. Źródło: Wikimedia Commons.

-Również w przypadku wektorów jednostkowych można wykonać wszystkie operacje sum, odejmowania i mnożenia wektora, które są wykonane przez zwykłe wektory. Dlatego ważne jest pomnożenie wektora jednostki przez skalar, a także przeprowadzić produkt punktowy i produkt krzyżowy.

-Z wektorem jednostkowym w określonym kierunku, można również wyrazić inne wektory, które są również zorientowane w tym kierunku.

Wektory jednostkowe w przestrzeni

Aby wyrazić dowolny wektor w przestrzeni lub w płaszczyźnie, możesz użyć zestawu jednolitych wektorów prostopadłych do siebie, które tworzą podstawę ortonormalną. Każdy z trzech preferencyjnych kierunków przestrzeni ma swój własny wektor jednostkowy.

Wróćmy do przykładu sił skierowanych wzdłuż osi poziomej. Jest to oś x, która ma dwie możliwości: kierunek po prawej i kierunku po lewej stronie. Załóżmy, że na osi x znajduje się wektor jednostkowy i skierowany w prawo, który możemy oznaczyć dowolną z tych form:

Może ci służyć: model atomowy Thomson: Charakterystyka, postulaty, cząstki subatomowe

Każdy z nich jest ważny. Załóżmy teraz siłę F₁ wielkości 5 N wzdłuż tej osi i skierowana w prawo, taką siłę można wyrazić jako:

Gdyby siła była skierowana wzdłuż osi x, ale w przeciwnym kierunku, to znaczy do lewej, wówczas do ustalenia tej różnicy można zastosować znak ujemny.

Na przykład siła wielkości 8 N, znajdująca się na osi x i skierowana w lewo byłaby taka:

Lub tak:

A dla wektorów, które nie są skierowane wzdłuż osi kartezja.

Jak usunąć/obliczyć wektor jednostki?

Aby obliczyć wektor jednostki w kierunku dowolnego dowolnego wektora v, Zastosowana jest następująca formuła:

Gdzie:

Jest to moduł lub wielkość wektora v, którego kwadrat jest obliczany w ten sposób:

|v|² = (v_X)² +  (v_I)²+  (v_z)²

Arbitralny wektor pod względem wektora jednostki

Alternatywnie wektor v Można to wyrazić w następujący sposób:

To znaczy produkt jego modułu przez odpowiedni wektor jednostki. Dokładnie to zostało zrobione wcześniej, mówiąc o sile 5 N wielkości skierowanej wzdłuż pozytywnej osi x.

Reprezentacja graficzna

Graficznie, to, co mówi się na tym obrazie, gdzie wektor v Jest w kolorze niebieskim, a odpowiedni wektor jednostki w jego kierunku jest na czerwono.

W tym przykładzie wektor v Ma wielkość większą niż wektor jednostki, ale wyjaśnienie jest nawet ważne, jeśli tak się nie stanie. Innymi słowy, możemy mieć wektory, które są na przykład 0.25 -krotność wektora jednostki.

Może ci służyć: waga (fizyczna): obliczenia, jednostki, przykłady, ćwiczenia

Przykłady wektorów jednostkowych

Wektory jednostki prostopadłowej I, J i K

Jak widzieliśmy wcześniej, wektory jednostki prostopadłe Siema, J I k Są one bardzo przydatne do reprezentowania dowolnego innego wektora w płaszczyźnie lub przestrzeni i przeprowadzania operacji wektorowych. Pod względem wspomnianego wektora arbitralny wektor V jest reprezentowany jako:

v = v_X Siema + v_I J + v_z k

Gdzie v_X, v_I i v_z są prostokątnymi elementami wektora v, które są wspinaczami -Bold, nie są używane do reprezentowania ich w drukowanym tekście-.

prawo Coulomba

Wektory jednolitowe pojawiają się często w fizyce. Tam mamy na przykład prawo Coulomba, które ilościowo opisuje interakcję między dwoma specyficznymi ładunkami elektrycznymi.

Wskazuje, że siła F przyciągania lub odpychania między tymi obciążeniami jest proporcjonalne do ich produktu, odwrotnie proporcjonalne do kwadratu odległości, który je oddziela i jest skierowany w kierunku wektora jednostki, który łączy obciążenia.

Ten wektor jest zwykle reprezentowany przez:

A prawo Coulomba jest takie, w formie wektorowej:

Gdzie k Jest to stała elektrostatyczna, Q₁ I Q₂ Są to ładunki i R Oddziela je odległość.

Ćwiczenie rozwiązane

Znajdź wektor jednostki w kierunku wektora v = 5Siema + 4J -8k, Podane w arbitralnych jednostkach.

Rozwiązanie

Powyżej definicja jednolitego wektora jest stosowana powyżej:

Ale najpierw musisz obliczyć moduł wektorowy, który, jak ma trzy komponenty, jest określany przez:

|v|² = (v_X)² +  (v_I)² +  (v_z)²

Przebywający:

|v|² = (5)² +  (4)² +  (-8)²= 25 + 16 + 64 = 105

Dlatego moduł v Jest:

|v| = √105

Szukany jednolity wektor jest po prostu:

To w końcu prowadzi nas do:

v = 0.488 Siema + 0.390 J - 0.781 k

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
2. Bedford, 2000. DO. Mechanika inżynierii: statyczne. Addison Wesley.
3. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. Pod redakcją Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fizyka. 2. Wyd. McGraw Hill.
5. Resnick, r. (1999). Fizyczny. Tom. 1. Wydanie trzecie. po hiszpańsku. Continental Editorial Company S.DO. c.V.