Ciągłe cechy zmienne, przykłady i ćwiczenia

Zmienna ciągła Jest to taki, który może przyjmować nieskończoną liczbę wartości numerycznych między dwiema danymi wartościami, nawet jeśli te dwie wartości są dowolnie bliskie. Są używane do opisania wymiernych atrybutów; na przykład wysokość i waga. Wartości pobrane przez zmienną ciągłą mogą być liczbami wymiernymi, liczbami rzeczywistymi lub liczbami złożonymi, chociaż ten ostatni przypadek jest rzadszy w statystykach. 

Główną cechą zmiennych ciągłych jest to, że między dwiema wartościami racjonalnymi lub rzeczywistymi można zawsze znaleźć, a między innymi a pierwszą można znaleźć inną wartość, a więc nieokreślony w nieskończoność.

Rysunek 1. Krzywa reprezentuje ciągły rozkład, a słupki dyskretnie. Źródło: Pixabay

Załóżmy na przykład zmienną wagową w grupie, w której największa waga ma 95 kg i najniższą masę 48 kg; Byłby to zakres zmiennej, a liczba możliwych wartości jest nieskończona.

Na przykład między 50,00 kg a 50,10 kg może wynosić 50,01. Ale między 50,00 a 50,01 miara może wynosić 50 005. To jest zmienna ciągła. Z drugiej strony, jeśli w możliwych miarach masy ustalono pojedynczą dokładność dziesiętną, zastosowana zmienna byłaby dyskretna.

Zmienne ciągłe należą do kategorii zmiennych ilościowych, ponieważ mają powiązaną wartość numeryczną. Z tą wartością numeryczną możliwe jest wykonywanie operacji matematycznych, od arytmetyki po metody obliczeń nieskończenie małego. 

[TOC]

Przykłady

Większość zmiennych fizyki to zmienne ciągłe, wśród nich możemy nazwać: długość, czas, prędkość, przyspieszenie, energia, temperatura i inne.

Zmienne ciągłe i zmienne dyskretne

W statystykach można zdefiniować różne rodzaje zmiennych, zarówno jakościowe, jak i ilościowe. Zmienne ciągłe należą do tej ostatniej kategorii. Z nimi możliwe jest wykonanie operacji arytmetycznych i obliczeniowych.

Na przykład zmienna H, odpowiadający osobom o wysokości od 1,50 m do 1,95 m, jest to zmienna ciągła. 

Porównajmy tę zmienną z tą drugą: liczba razy, które są drogie w uruchomieniu waluty, którą zadzwonimy N.

Zmienna N Możesz jednak wziąć wartości między 0 a nieskończonością, N Nie jest to zmienna ciągła, ponieważ nie może przyjąć wartości 1.3 lub 1,5, ponieważ między wartościami 1 i 2 nie ma innych. To jest przykład Zmienna dyskretna.

Ćwiczenie zmiennych ciągłych

Rozważ następujący przykład: maszyna wytwarza dopasowanie fosforu i pakuje je w pudełku. Zdefiniowano dwie zmienne statystyczne:

Może ci służyć: proces izobaryczny: formuły, równania, eksperymenty, ćwiczenia

Zmienna 1: L = długość zmniejszania.

Zmienna 2: n = liczba świń na pudełko.

Nominalna długość dopasowań wynosi 5,0 cm z tolerancją 0,1 cm. Liczba świń na pudełko wynosi 50 z tolerancją 3.

a) Wskaż zakres wartości, które mogą przyjąć L I N.

b) Ile wartości możesz wziąć L?

c) Ile wartości możesz wziąć N?

Powiedz w każdym przypadku, jeśli jest to dyskretna lub ciągła zmienna.

Rozwiązanie

Wartości L Są one rozumiane w przedziale [5,0-0,1; 5,0+0,1]; to znaczy, że wartość L jest w przedziale [4,9 cm; 5.1 cm] i zmienna L Możesz wziąć nieskończone wartości między tymi dwoma miarami. Jest to wówczas zmienna ciągła.

Wartość zmiennej N jest w przedziale [47; 53]. Zmienna N Może przyjmować tylko 6 możliwych wartości w przedziale tolerancji, jest to wówczas dyskretna zmienna.

Ćwiczenie rozkład prawdopodobieństwa

Jeśli oprócz ciągłości, wartości wzięte przez zmienną związały się z pewnym prawdopodobieństwem występowania, to jest to a Ciągła zmienna losowa. Bardzo ważne jest rozróżnienie, czy zmienna jest dyskretna czy ciągła, ponieważ modele probabilistyczne mające zastosowanie do siebie są różne.

Ciągła zmienna losowa jest całkowicie zdefiniowana, gdy wartości, które mogą zakładać, są znane, a prawdopodobieństwo, że każda z nich musi się zdarzyć.

-Ćwiczenie 1 prawdopodobieństwa

Fabryka dopasowań czyni je w taki sposób, że długość kijów jest zawsze między wartościami 4,9 cm i 5,1 cm, a zero z tych wartości. Istnieje prawdopodobieństwo uzyskania drążka, który mierzy między 5,00 a 5,05 cm, chociaż moglibyśmy również wyodrębnić jeden z 5.0003 cm. Czy te wartości są równie prawdopodobne?.

Może ci służyć: gęstość względna: obliczenia, przykłady, ćwiczenia

Rozwiązanie

Załóżmy, że gęstość prawdopodobieństwa jest jednolita. Następnie wymieniono szanse na znalezienie fosforu o określonej długości:

-Że fosfor jest w zakresie [4,9; 5,1] ma prawdopodobieństwo = 1 (lub 100%), ponieważ maszyna nie pobiera dopasowań z tych wartości.

-Znalezienie fosforu, który wynosi od 4,9 do 5,0, ma prawdopodobieństwo = ½ = 0,5 (50%), ponieważ jest to połowa zakresu długości.

-A prawdopodobieństwo, że dopasowanie ma długość między 5,0 a 5,1, wynosi również 0,5 (50%)

-Wiadomo, że nie ma kijów fosforu o długości od 5,0 do 5,2. Prawdopodobieństwo: zero (0%).

Prawdopodobieństwo znalezienia kija w określonym zakresie

Teraz obserwujmy następujące prawdopodobieństwa p, aby uzyskać patyki, których długość jest pomiędzy L₁ i ja₂:

 P = (L₂ -L₁) /(L_Max - L_min)

-P, że mecz ma długość między 5,00 a 5,05, jest oznaczone jako P ([5.00; 5.05]):

P ([5,00; 5,05]) = (5,05 - 5,00)/(5,1 - 4,9) = 0,05/0,2 = ¼ = 0,25 (25%)

-P, że Cerrillo ma długość od 5,00 do 5,01, wynosi:

P ([5,00; 5,01]) = (5,00 - 5,01)/(5,1 - 4,9) = 0,01/0,2 = 1/20 = 0,05 (5 %)

-P, że Cerrillo ma długość od 5000 do 5001, jest jeszcze niższe:

P (5000; 5 001) = 0,001/0,2 = 1/200 = 0,005 (0,5%)

Jeśli nadal zmniejszamy interwał, aby zbliżyć się do 5,00, prawdopodobieństwo, że drąż ma dokładnie 5,00 cm, wynosi zero (0%). Mamy prawdopodobieństwo znalezienia dopasowania w określonym zakresie.

Prawdopodobieństwo znalezienia kilku patyków w określonym zakresie

Jeśli zdarzenia są niezależne, prawdopodobieństwo, że dwa patyki znajdują się w określonym zakresie, jest wynikiem ich prawdopodobieństwa.

-Prawdopodobieństwo, że dwa patyki wynosi między 5,0 a 5,1, wynosi 0,5*0,5 = 0,25 (0,25%)

-Prawdopodobieństwo, że 50 patyków wynosi między 5,0 a 5,1, wynosi (0,5)^50 = 9 × 10^-16, czyli prawie zero.

-Prawdopodobieństwo, że 50 patyków wynosi od 4,9 do 5,1 wynosi (1)^50 = 1 (100%)

-Ćwiczenie 2 prawdopodobieństwa

W poprzednim przykładzie założyło się, że prawdopodobieństwo jest jednolite w danym przedziale, jednak nie zawsze tak jest.

Może ci służyć: ciśnienie hydrostatyczne: wzór, obliczenia, przykłady, ćwiczenia

W przypadku prawdziwej maszyny, która produkuje patyki, możliwość, że patyk jest w wartości centralnej, jest większa niż w jednej z ekstremalnych wartości. Z matematycznego punktu widzenia jest to modelowane z funkcją f (x) znaną jako gęstość prawdopodobieństwa.

Prawdopodobieństwo, że miara jest między A i B, jest obliczane przez zdefiniowaną całkę funkcji F (x) między A i B. 

Na przykład załóżmy, że chcemy znaleźć funkcję f (x), która reprezentuje jednolity rozkład między wartościami 4.9 i 5.1 ćwiczenia 1. 

Jeśli rozkład prawdopodobieństwa jest jednolity, wówczas F (x) jest równy stałej C, co jest określane przy przyjmowaniu całki między 4,9 a 5,1 C. Ponieważ ta całka jest prawdopodobieństwem, więc wynik musi wynosić 1.

Rysunek 2. Jednolita gęstość prawdopodobieństwa. (Własne opracowanie)

Co oznacza, że ​​C jest wart 1/0,2 = 5. Innymi słowy, funkcja gęstości jednolitej prawdopodobieństwa wynosi f (x) = 5, jeśli 4,9 x x 5,1 i 0 z tego zakresu. Rysunek 2 pokazuje funkcję gęstości jednolitej.

UWAGA, jak w odstępach tej samej szerokości (na przykład 0,02) prawdopodobieństwo jest takie samo w środku, jak na końcu zakresu zmiennych L (Długość marynaty).

Bardziej realistyczny model byłby funkcją gęstości prawdopodobieństwa jako następujące:

-f (x) = -750 ((x-5,0)^2-0,01) Jeśli 4,9 x x 5,1

-0 poza tym zakresem 

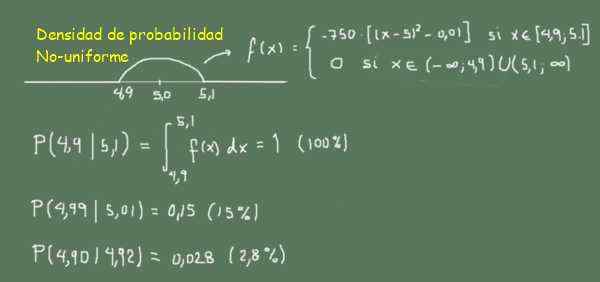Rysunek 3. Funkcja gęstości prawdopodobieństwa niejednorodności. (Własne opracowanie)

Na rycinie 3 można zaobserwować, ponieważ prawdopodobieństwo znalezienia drążków między 4,99 a 5,01 (szerokość 0,02) jest większe niż znajdowanie patyków między 4,90 a 4,92 (szerokość 0,02)

Bibliografia

1. Dinov, IVO. Dyskretne zmienne losowe i rozkłady prawdopodobieństwa. Odzyskane z: Stat.UCLA.Edu
2. Dyskretne i ciągłe zmienne losowe. Odzyskane z: OCW.MIT.Edu
3. Dyskretne zmienne losowe i rozkłady prawdopodobieństwa. Odzyskane z: strona główna.DDM.Uiowa.Edu
4. H. Peshro. Wprowadzenie do prawdopodobieństwa. Odzyskane z: Kurs prawdopodobieństwa.com
5. Mendenhall, w. 1978. Statystyka administracji i ekonomii. Ibero -american Group. 103-106.
6. Losowe problemy zmienne i modele prawdopodobieństwa. Odzyskane z: Ugr.Jest.
7. Wikipedia. Zmienna ciągła. Wyzdrowiał z Wikipedii.com
8. Wikipedia. Zmienna statystyczna. Wyzdrowiał z Wikipedii.com.