Historia trójkątów, elementy, klasyfikacja, właściwości

trójkąty Są płaskie i zamknięte postacie geometryczne, które składają się z trzech stron. Trójkąt jest określany przez trzy linie, które są wycięte dwa do dwóch, tworząc się ze sobą trzy kąty. Trójkątna postać, pełna symboliki, jest obecna w niezliczonych obiektach i jako element konstrukcji.

Pochodzenie trójkąta jest utracone w historii. Z dowodów archeologicznych wiadomo, że prymitywna ludzkość znała go dobrze, ponieważ pozostałości archeologiczne potwierdzają, że był używany w narzędzia i broni.

Rysunek 1. Trójkąty. Źródło: Public DomeAnpartures.

Oczywiste jest również, że starożytni Egipcjanie mieli solidną wiedzę na temat geometrii, a zwłaszcza o trójkątnej formie. Zostali wcielone w elementy architektoniczne swoich monumentalnych konstrukcji.

W papirusie Rhind istnieją wzory do obliczania trójkątów i obszarów trapezowych, a także niektórych tomów i innych koncepcji podstawowej trygonometrii.

Z drugiej strony wiadomo, że Babilończycy byli w stanie obliczyć obszar trójkąta i innych postaci geometrycznych, których używali do celów praktycznych, takich jak podziały lądu. Byli również świadomi wielu właściwości trójkątów.

Jednak to starożytni Grecy usystematyzowali wiele częstych koncepcji geometrycznych, choć znaczna część tej wiedzy nie była wyłączna, ponieważ z pewnością była dzielona z innymi starożytnymi cywilizacjami.

[TOC]

Elementy trójkąta

Elementy dowolnego trójkąta są wskazane na poniższym rysunku. Istnieją trzy: wierzchołki, boki i kąty.

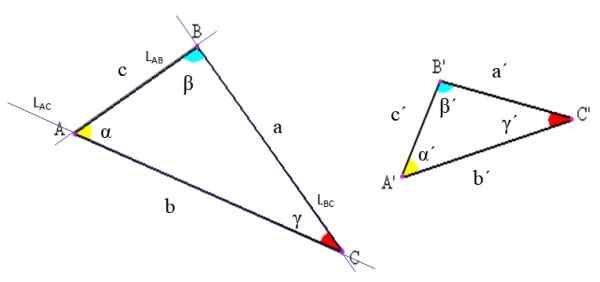Rysunek 2. Notacja trójkątów i ich elementów. Źródło: Wikimedia Commons, zmodyfikowane przez F. Zapata

-Wierzchołki: Są to punkty przecięcia linii, których segmenty określają trójkąt. Na przykład na górnej figurze linia L_AC który zawiera segment prądu przemiennego, przecina linię L_Ab który zawiera segment ab właśnie w punkcie a.

-boki: Pomiędzy każdą parą wierzchołków narysowany jest segment linii, który stanowi jedną stronę trójkąta. Ten segment może być oznaczony literami końcowymi lub za pomocą konkretnej litery, aby to nazwać. W przykładzie ryc. 2 strona AB jest również nazywana „C”.

-Kąty: Między każdą stroną ze wspólnym wierzchołkiem pochodzi kąt, którego wierzchołek pokrywa. Kąt jest zazwyczaj oznaczony grecką literą, jak stwierdzono na początku.

Aby zbudować określony trójkąt o danym kształcie i rozmiarze, po prostu mieć niektóre z następujących zestawów danych:

-Trzy strony, dość oczywiste w przypadku trójkąta.

-Dwie strony i kąt między nimi, a pozostała strona jest natychmiast narysowana.

-Dwa kąty (wewnętrzne) i bok między nimi. W związku z tym rysowane są dwie brakujące strony, a trójkąt jest gotowy.

Notacja

Zasadniczo w notacji trójkątów stosowane są następujące konwencje: wierzchołki są wskazane literami kapitałowymi, boki z małymi literami łacińskimi i kątami greckim literami (patrz ryc. 2).

W ten sposób trójkąt jest nazwany zgodnie z jego wierzchołkami. Na przykład trójkąt po lewej na ryc. 2 to trójkąt ABC, a ten po prawej jest trójkąt a'b'c '.

Możliwe jest również użycie innych zapisów; Na przykład kąt α na rycinie 2 jest oznaczony jako BAC. Zauważ, że litera wierzchołka idzie na środku, a litery są zapisane w przeciwnym kierunku do igieł zegarowych.

Może ci służyć: rozgraniczenie problemu

Innym razem umieszcza się akcent obwodowy, aby oznaczyć kąt:

Lub używany jest symbol ∠, ponieważ poprzednia notacja może nie być łatwa w druku, a następnie litera odpowiadająca wierzchołkowi:

α = ∠A

Rodzaje trójkątów

Istnieje kilka kryteriów klasyfikacji trójkątów. Najbardziej zwykle jest sklasyfikowanie ich zgodnie ze miarą ich boków lub zgodnie z miarą ich stron. W zależności od miary ich boków trójkąty mogą być: skaleny, izosceli lub równoboje:

-Różnoboczny: Jego trzy strony są różne.

-Równoramienny: Ma dwie różne strony i jedną.

-Równoboczny: Trzy strony są takie same.

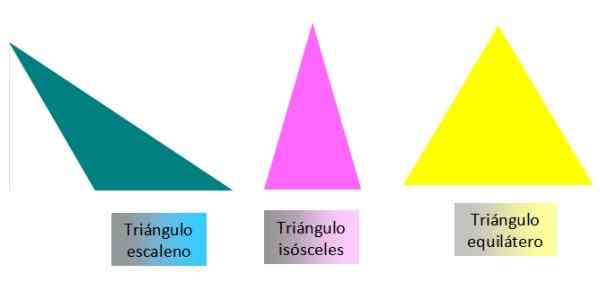Rysunek 3. Klasyfikacja trójkątów po ich bokach. Źródło: f. Zapata

Zgodnie z miarą ich kątów trójkąty nazywane są tak:

-Rozwarty, Jeśli jeden z wewnętrznych kątów jest większy niż 90º.

-Acutangle, Gdy trzy wewnętrzne kąty trójkąta są ostre, to znaczy mniej niż 90º

-Prostokąt, W przypadku, gdy jeden z jego wewnętrznych stron jest wart 90º. Boki, które tworzą 90º, są nazywane Catetos, a przeciwną stroną do kątu jest hipotencja.

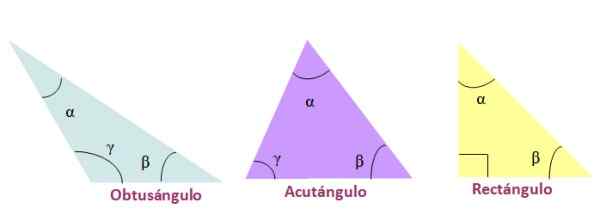Rysunek 4. Klasyfikacja trójkątów pod kątem wewnętrznym. Źródło: f. Zapata.

Zgodność trójkątów

Kiedy dwa trójkąty mają ten sam kształt i mają równy rozmiar, mówi się, że są one zgodne. Oczywiście zgodność jest związana z równością, więc dlaczego w geometrii mówimy o „dwóch przystających trójkątach” zamiast „dwóch równych trójkątach”?

Cóż, preferowane jest użycie terminu „zgodność”, aby trzymać się prawdy, ponieważ dwa trójkąty mogą mieć ten sam kształt i rozmiar, ale być zorientowany inaczej w płaszczyźnie (patrz ryc. 3). Z punktu widzenia geometrii nie byłyby już ściśle takie same.

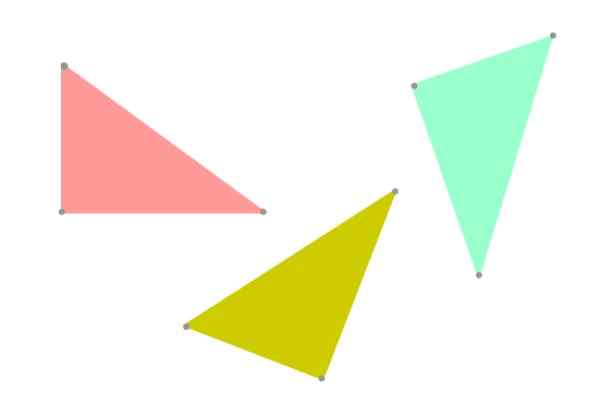Rysunek 5. Przystające trójkąty, ale niekoniecznie takie same, ponieważ jego orientacja w samolocie jest inna. Źródło: f. Zapata.

Kryteria zgodności

Dwa trójkąty są zgodne, jeśli pojawia się którekolwiek z następujących sytuacji:

-Trzy strony mierzą to samo (znowu jest to najbardziej oczywiste).

-Mają dwie identyczne strony i z tym samym kątem między nimi.

-Oba mają dwa identyczne kąty wewnętrzne, a strona między tymi kątami jest taka sama.

Jak widać, chodzi o dwa trójkąty spełniające niezbędne warunki, aby podczas ich budowy ich kształt i rozmiar były dokładnie takie same.

Kryteria zgodności są bardzo przydatne, ponieważ w praktyce niezliczone części i części mechaniczne muszą być produkowane szeregowo, aby ich środki i forma były dokładnie takie same.

Podobieństwo trójkątów

Trójkąt jest podobny do innego, jeśli mają ten sam kształt, nawet jeśli mają różny rozmiar. Aby upewnić się, że kształt jest taki sam, konieczne jest, aby kąty wewnętrzne miały tę samą wartość i że boki są proporcjonalne.

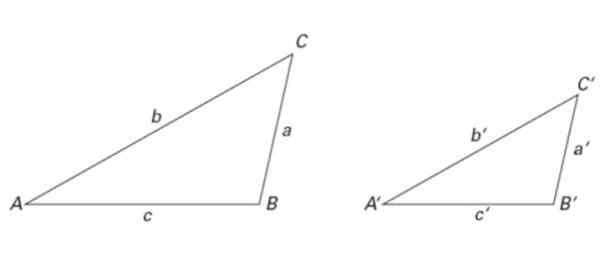Rysunek 6. Dwa podobne trójkąty: ich rozmiary różnią się, ale ich proporcje są takie same. Źródło: f. Zapata.

Trójkąty na ryc. 2 są również podobne, a także te na rycinie 6. Zatem:

∠ A = ∠ A ', ∠ B = ∠ B 'i ∠ C = ∠ C '

Jeśli chodzi o boki, spełnione są następujące przyczyny podobieństwa:

a/a '= b/b' = c/c '

Nieruchomości

Podstawowe właściwości trójkątów są następujące:

-Suma wewnętrznych kątów dowolnego trójkąta wynosi zawsze 180º.

-W przypadku każdego trójkąta suma jego kątów zewnętrznych jest równa 360 °.

Może ci służyć: badania podstawowe: cechy, definicja, przykłady

- Zewnętrzny kąt trójkąta jest równy sumie dwóch kątów wewnętrznych, które nie sąsiadują z tym kątem.

Twierdzenia

Pierwsze twierdzenie o takich

Są one przypisywane greckie filozof i matematyka. Pierwszy z nich ustanawia:

Jeśli kilka równoległych linii przecięło dwie linie poprzeczne, określają segmenty proporcjonalne.

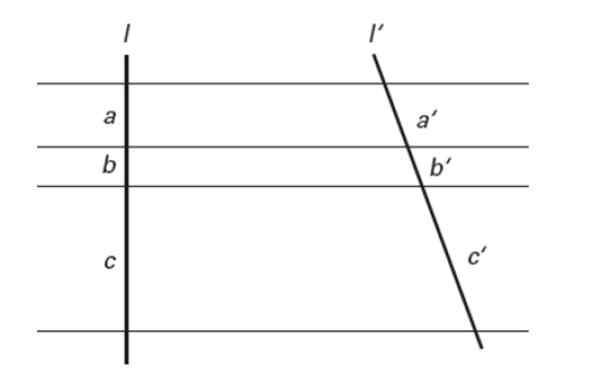Rysunek 7. Twierdzenie opowieści. Źródło: f. Zapata.

Innymi słowy:

a/a '= b/b' = c/c '

Pierwsze twierdzenie takiego ma zastosowanie do trójkąta, na przykład po lewej stronie znajduje się niebieski trójkąt ABC, który jest wycinany przez czerwone paralele po prawej:

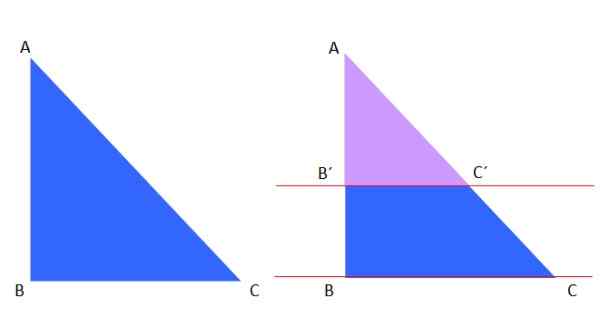Cyfra 8. Twierdzenie o takich i podobnych trójkąt.

Fioletowy trójkąt fioletowy jest podobny do trójkąta ABC, dlatego, zgodnie z takim twierdzeniem, można napisać następujące:

AB '/AC' = AB/AC

I jest to zgodne z tym, co wyjaśniono powyżej w segmencie podobieństwa trójkątów. Nawiasem mówiąc, równoległe linie mogą być również pionowe lub równoległe do przeciwprostokątnej i otrzymuje się podobne trójkąty.

Drugie twierdzenie o tym

Twierdzenie to odnosi się również do trójkąta i obwodu środkowego lub, jak pokazane poniżej. Na tej figurze AC jest średnicą obwodu, a B jest jej punktem, różniącym się od A i B.

Drugie twierdzenie takiego stwierdza, że:

Kąt między segmentami AB i BC wynosi zawsze 90º, dlatego trójkąt ABC to prostokąt.

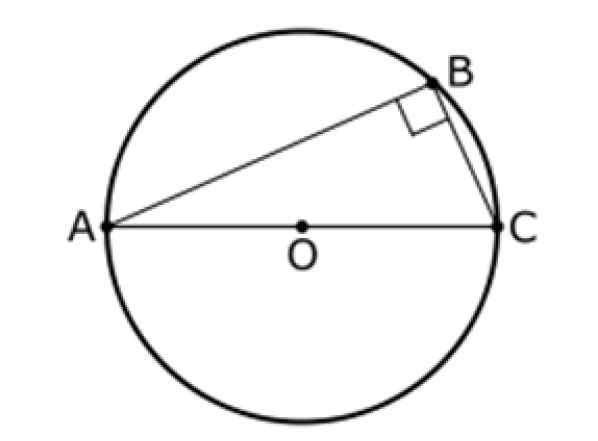Rysunek 9. Drugie twierdzenie takiego. Źródło: Wikimedia Commons. Inductiveload [domena publiczna].

twierdzenie Pitagorasa

To jedno z najbardziej znanych twierdzeń w historii. Jest to spowodowane greckim matematykiem Pitagoras z Samos (569–475 do. C.) i ma zastosowanie do prawego trójkąta. Mówi więc:

Suma kwadratów długości kategorii trójkąta prostokąta jest równa długości hipotenu wysokości do kwadratu.

Jeśli weźmiemy jako przykład, niebieski trójkąt z ryc. 8 lub fioletowego trójkąta, ponieważ oba są prostokątami, można powiedzieć, że:

AC² = Ab² + pne² (Niebieski trójkąt)

Ac '² = Ab '² + PNE '² (Fioletowy trójkąt)

Obszar trójkąta

Obszar trójkąta jest podawany przez iloczyn jego podstawy Do i jego wysokość H, podzielone przez 2. A za trygonometrią tę wysokość można zapisać jako H = b sinθ.

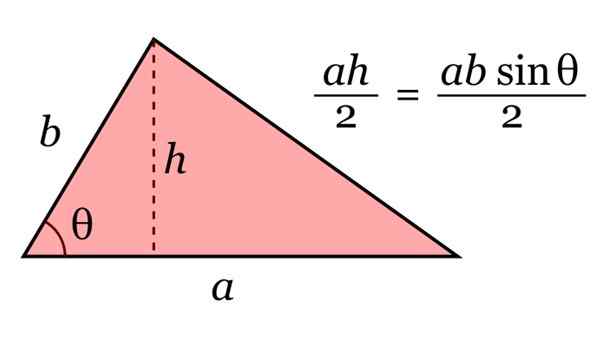Rysunek 10. Obszar trójkąta. Źródło: Wikimedia Commons.

Przykłady trójkątów

Przykład 1

Mówi się, że poprzez swoje pierwsze twierdzenie, takie udało się zmierzyć wysokość wielkiej piramidy w Egipcie, jedną z 7 cudów starożytnego świata, mierząc cień, który przewidział na ziemi, i ten, w którym przewiduje udział w pakiecie. Ziemia.

Jest to schemat procedury, a następnie taki:

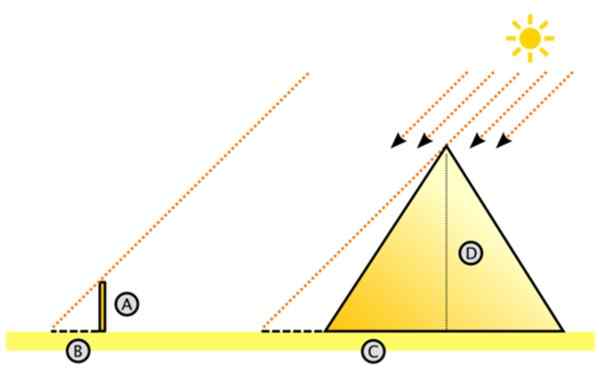Rysunek 11. Plan pomiaru wysokości wielkiej piramidy przez podobieństwo trójkątów. Źródło: Wikimedia Commons. Dake [CC BY-SA 3.0 (http: // creativeCommons.Org/licencje/by-sa/3.0/]]

Tak słusznie przypuszczalnie, że promienie słońca wpływają równolegle. Mając to na uwadze, wyobrażał sobie wielki prawy trójkąt.

Istnieje wysokość piramidy, a C jest odległością na ziemi mierzonej od środka do cienia rzutowanego przez piramidę na pustynnej podłodze. Mierzenie C może być pracochłonne, ale z pewnością jest łatwiejsze niż pomiar wysokości piramidy.

Po lewej stronie znajduje się mały trójkąt, od kotów A i B, gdzie A jest wysokością palika utkniętego pionowo na podłodze, a B to cień, który projektuje. Obie długości są mierzalne, podobnie jak C (C jest równa długości cienia + połowa długości piramidy).

Może ci służyć: jakie są dotykowe bodźce?

Następnie przez podobieństwo trójkątów:

A/B = D/C

A wysokość wielkiej piramidy okazuje się być: d = c.(A/B)

Przykład 2

Zbroja budowlana cywilna to konstrukcje oparte na cienkich lub metalowych prętach prostych, które są używane jako wsparcie w wielu budynkach. Są one również znane jako kratki, kratownicy lub siatkowe (Kratownica po angielsku).

W nich trójkąty są zawsze obecne, ponieważ słupki są ze sobą powiązane w punktach zwanych węzłami, które można naprawić lub wyartykułować.

Rysunek 12. Trójkąt jest obecny w ramie tego mostu. Źródło: Pxhere.

Przykład 3

Metoda znana jako triangulacja pozwala uzyskać lokalizację niedostępnych punktów, znając inne łatwiejsze odległości do pomiaru, pod warunkiem, że powstaje trójkąt, który obejmuje wśród jego wierzchołków pożądaną lokalizację.

Na przykład, na poniższej liczbie, którą chcesz wiedzieć, w którym momencie morze jest statkiem, oznaczonym jako B.

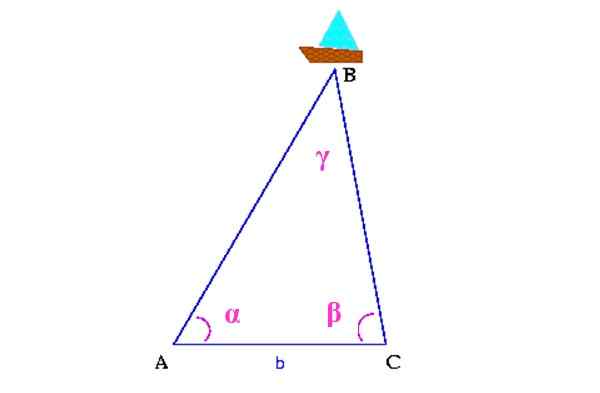Rysunek 13. Schemat triangulacji do zlokalizowania statku. Źródło: Wikimedia Commons. Colette [CC BY-SA 3.0 (http: // creativeCommons.Org/licencje/by-sa/3.0/]]

Po pierwsze, mierzona jest odległość między dwoma punktami na wybrzeżu, która na rysunku wynosi A i C. Następnie musisz określić kąty α i β, za pomocą a teodolit, Urządzenie, które służy do pomiaru kąty pionowych i poziomych.

Z wszystkimi tymi informacjami zbudowany jest trójkąt, na którego górnym wierzchołku jest statek. Zmniejszyłoby to kąt γ za pomocą.

Ćwiczenia

Ćwiczenie 1

Na pokazanym rysunku promienie słoneczne są równoległe. W ten sposób 5 -metodeczne drzewo wyświetla 6 -metrowy cień na ziemi. W tym samym czasie cień budynku wynosi 40 metrów. Zgodnie z takiego twierdzenia, znajdź wysokość budynku.

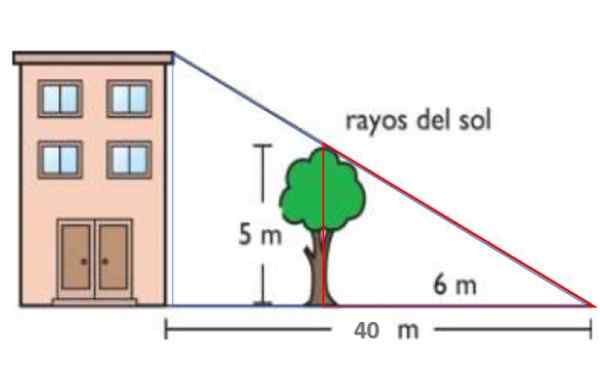Rysunek 14. Program na rok rozwiązany 1. Źródło: f. Zapata.

Rozwiązanie

Czerwony trójkąt ma strony odpowiednio 5 i 6 metrów, podczas gdy niebieski ma wysokość H -Wysokość budynku i podstawy 40 metrów. Dlatego oba trójkąty są podobne:

H / 40 = 5/6 → H = 40.(5/6) M = 33.3 m

Ćwiczenie 2

Musisz znać poziomy odległość między dwoma punktami DO I B, Ale znajdują się na bardzo nieregularnym terenie.

W przybliżeniu w punkcie środkowym (p_M) Z tej krainy wyróżnia się punkt 1.75 metrów wysokości. Jeśli miara taśmy wskazuje 26 metrów długości mierzonej od A do pozycji i 27 metrów od B do tego samego punktu, znajdź odległość Ab.

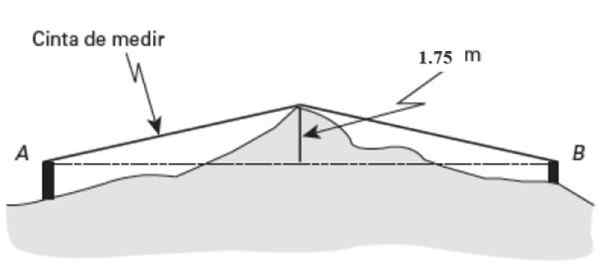Rysunek 15. Schemat ćwiczeń rozwiązanych 2. Źródło: Jiménez, r. Matematyka II. Geometria i trygonometria.

Rozwiązanie

Twierdzenie Pitagorasa jest stosowane do jednego z dwóch trójkątów prostokątów na rysunku. Zaczynając od tego po lewej:

Hipotenuse = c = 26 metrów

Wysokość = a = 1.75 metrów

AP_M = (26² - 1.75²)^1/2 = 25.94 m

Teraz Pitagoras jest stosowany w prawym trójkącie, tym razem c = 27 metrów, a = 1.75 metrów. Z tymi wartościami:

BP_M= (27² - 1.75²)^1/2 = 26.94 m

Odległość AB dodaje te wyniki:

AB = 25.94 m +26.94 m = 52.88 m.

Bibliografia

1. Baldor, J. DO. 1973.Płaska i przestrzeń geometria. Cultural American Cultural.
2. BARREDO, zm. Geometria trójkąta. Odzyskane z: ficus.pntic.Mec.Jest.
3. Jiménez, r. 2010. Matematyka II. Geometria i trygonometria. Druga edycja. osoba.
4. Wentworth, G. Geometria planety. Odzyskane z: Gutenberg.org.
5. Wikipedia. Trójkąt. Odzyskane z: jest. Wikipedia.org.