Trójkąt acutangle

Co to są trójkąty acutangulus?

Trójkąty Acutangulus Są to te, których trzy wewnętrzne kąty są ostrymi kątami; to znaczy miara każdego z tych kąta jest mniejsza niż 90 ° stopni. Nie mając żadnego kątu prostego, mamy, że twierdzenie Pitagorasa nie jest spełnione dla tej liczby geometrycznej.

Dlatego jeśli chcemy mieć jakieś informacje o którejkolwiek z jego stron lub kątów, konieczne jest użycie innych twierdzeń, które pozwalają nam mieć dostęp do tych danych. Ci, których możemy użyć, to twierdzenie piersi i twierdzenie cosinus.

Charakterystyka trójkąta Acutangle

Wśród cech, które posiada ta geometryczna postać, możemy podkreślić te, które są podane przez prosty fakt bycia trójkątem. Wśród nich musimy:

- Trójkąt to wielokąt, który ma trzy strony i trzy kąty.

- Suma trzech wewnętrznych kąty wynosi 180 °.

- Suma dwóch jego stron jest zawsze większa niż trzecia.

Jako przykład, zobaczmy następujący trójkąt ABC. Ogólnie rzecz biorąc, identyfikujemy ich strony z małą literą i kątami z kapitałem, aby strona i ich przeciwny kąt miały ten sam list.

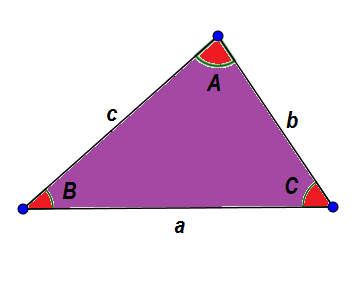
Ze względu na podane cechy wiemy, że:

A + B + C = 180 °

A + B> C, A + C> B i B + C> A

Główną cechą, która odróżnia ten typ trójkąta od reszty, jest to, że, jak już wspomnieliśmy, jego wewnętrzne kąty są ostre; Oznacza to, że miara każdego z jego kąta jest mniejsza niż 90 °.

Trójkąty acutangulus wraz z tępymi trójkątami (w których jeden z jego kąta ma miarę większą niż 90 °), są częścią zestawu ukośnych trójkątów. Ten zestaw jest tworzony przez trójkąty, które nie są prostokątami.

Może ci służyć: jakie są elementy przypowieści? (Części)

Będąc częścią ukośnych trójkątów, musimy rozwiązać problemy, w których interweniowanie Trójkąta Acutangulus muszą używać twierdzenia o piersi i cosinus.

Twierdzenie o piersi

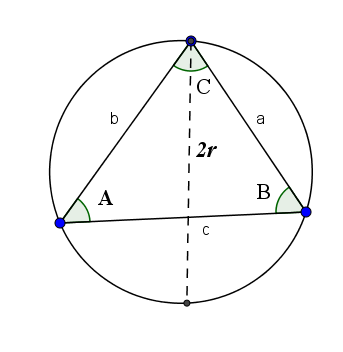
Twierdzenie o piersi potwierdza, że ​​przyczyna z jednej strony z łopatą jego przeciwnego kąta jest równa dwa razy większy promień koła utworzony przez trzy wierzchołki wspomnianego trójkąta. To jest do powiedzenia:

2r = a/sin (a) = b/sen (b) = c/sen (c)

Twierdzenie Coseno

Z drugiej strony twierdzenie Coseno daje nam te trzy równości dla każdego trójkąta ABC:

Do²= b² + C² -2BC*cos (a)

B²= a² + C² -2ac*cos (b)

C²= a² + B² -2AB*cos (c)

Te twierdzenia są również znane również jako prawo zatoki i prawo cosinus.

Kolejną cechą, którą możemy podać o ostrożnych trójkątach, jest to, że dwa z nich są takie same, jeśli spełniają którekolwiek z następujących kryteriów:

• Jeśli mają wszystkie trzy strony.
• Jeśli mają stronę i dwa kąty równe sobie.
• Jeśli mają dwie strony i równy kąt.

Rodzaje trójkątów Acutángulos

Trójkąty Acutangulus można klasyfikować zgodnie z ich stronami. To mogą być:

Trójkąty równoboczne acutanglos

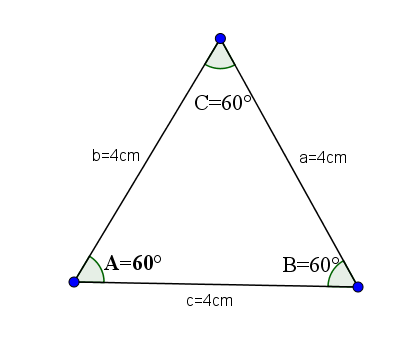
Są to ostre trójkąty, które mają wszystkie swoje równe strony, a zatem wszystkie ich wewnętrzne kąty mają tę samą wartość, czyli A = B = C = 60 ° stopni.

Jako przykład, weźmy następujący trójkąt, którego strony a, b i c mają wartość 4.

Isosceles acutángulos trójkąty

Te trójkąty, oprócz ostrej kąty wewnętrznych, mają charakterystykę posiadania dwóch ich równych stron i trzecie.

Przykładem tego typu trójkątów może być taki, którego podstawa to 3, a pozostałe dwie strony mają wartość 5. Przy tych pomiarach miałoby to kąty przeciwne równym bokom o wartości 72,55 °, a przeciwny kąt podstawy wynosiłby 34,9 °.

Może ci służyć: kąt zerowy: definicja i cechy, przykłady, ćwiczenia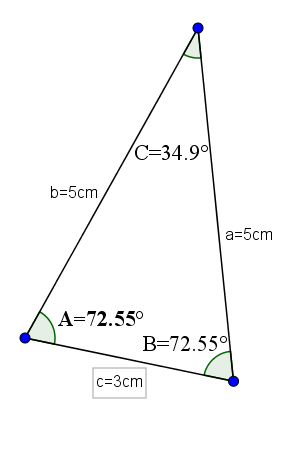

Scalene acutangulus trójkąty

To są trójkąty, które mają wszystkie swoje różne strony od dwóch do dwóch. Dlatego wszystkie jego kąty, oprócz mniej niż 90 °, są różne od dwóch do dwóch.

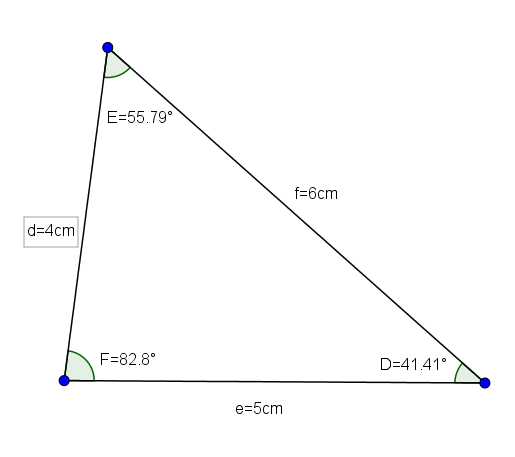
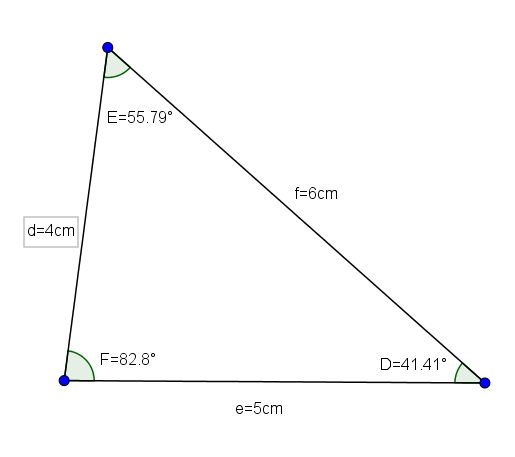
Trójkąt def (którego pomiary wynoszą d = 4, e = 5 i f = 6, a jego kąty wynoszą d = 41,41 °, e = 55,79 ° i F = 82,8 °) jest dobrym przykładem scalenowania trójkąta trucangle scalenge.

Rozwiązanie trójkątów

Jak powiedzieliśmy wcześniej, w przypadku rozwiązywania problemów, w których interweniuje trójkąty Acutangulus.

Przykład 1

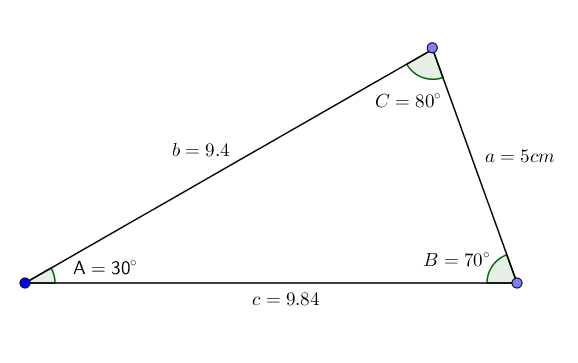
Biorąc pod uwagę trójkąt ABC o kątach A = 30 °, B = 70 ° i strona A = 5 cm, chcemy poznać wartość kąta C i boków B i C.

Pierwszą rzeczą, którą robimy, jest użycie faktu, że suma wewnętrznych kątów trójkąta wynosi 180 °, aby uzyskać wartość kąta C.

180 ° = A + B + C = 30 ° + 70 ° + C = 100 ° + C

Wyczyścimy C i mamy:

C = 180 ° - 100 ° = 80 °

Jak znamy trzy kąty i jedna strona, możemy użyć twierdzenia o piersi, aby określić wartość pozostałych stron. W przypadku twierdzenia musimy:

a/sin (a) = b/sen (b) i a/sen (a) = c/(sin (c)

Wyczyścimy równanie i musimy:

B = (a*sin (b))/sin (a) ≈ (5*0.940) / (0.5) ≈ 9.4

Teraz musimy tylko obliczyć wartość C. Postępujemy analogicznie jak w poprzedniej sprawie:

C = (a*sin (c))/sin (a) ≈ (5*0.984)/(0.5) ≈ 9.84

Dlatego otrzymujemy wszystkie dane trójkąta. Jak możemy zauważyć, ten trójkąt wchodzi do kategorii trójkąta skanowania.

Przykład 2

Biorąc pod uwagę trójkąt obrony z bokami D = 4 cm, E = 5 cm i f = 6 cm, chcemy znać wartość kątów wspomnianego trójkąta.

W tej sprawie wykorzystamy prawo cosinusa, które mówi nam, że:

Może ci służyć: suma kwadratów dwóch kolejnych liczb

D²= e² + F² - 2efcos (d)

Z tego równania możemy wyczyścić cos (d), co powoduje:

Cos (d) = ((4)² - (5)² -(6)²)/(-2*5*6) = 0.75

Stąd musimy dokować 41.41 °

Korzystanie z twierdzenia Senom mamy teraz następujące równanie:

D/(sin (d) = e/(sin (e)

Oczyszczanie sen (e), musimy:

sin (e) = e*sen (d)/d = (5*0.66)/4 ≈ 0.827

Stąd musimy.79 °

Wreszcie, stosując sumę wewnętrznych kątów trójkąta, wynosi 180 °, musimy.8 °.