Dyskretne transformowane właściwości, aplikacje, przykłady

Fourier dyskretnie przekształcono Jest to metoda numeryczna stosowana do definiowania próbek związanych z częstotliwościami widmowymi, które tworzą sygnał. Bada okresowe funkcje w zamkniętych parametrach, w rezultacie rzucając kolejny dyskretny sygnał.

Aby uzyskać dyskretną transformację wściekłości z N Punkty, na dyskretnym sygnale, należy spełnić następujące 2 warunki w sekwencji X [n]

 x [n] = 0   N n - 1

Spełniając te warunki, dyskretna transformacja Fouriera można zdefiniować jako

TDF

Dyskretna transformacja Fouriera można zdefiniować jako pobieranie próbek w n punktach transformacji Fouriera.

[TOC]

Interpretacja dyskretnej transformacji Fouriera

Źródło: Pexels

Istnieją 2 punkty widzenia, z których wyniki uzyskane na sekwencji x można interpretować_S[n] poprzez dyskretną transformację Fouriera.

-Pierwszy odpowiada współczynnikom widmowym, znanym już serii Fouriera. Obserwuje się go w dyskretnych sygnałach okresowych, a próbki pokrywają się z sekwencją x_S[N].

-Drugi dotyczy widma dyskretnego sygnału aperiadowego, z próbkami odpowiadającymi sekwencji x_S[N].

Dyskretna transformacja jest podejściem do widma oryginalnego sygnału analogowego. Jego faza zależy od momentów pobierania próbek, a jego wielkość zależy od przedziału próbkowania.

Nieruchomości

Podstawy struktury algebraiczne stanowią logiczne podstawy następujących sekcji.

Liniowość

C . S_N → c . F[S_k]; Jeśli sekwencja zostanie pomnożona przez skalar, jej transformacja będzie również.

T_N + V_N = F [t_k]+F [v_k]; Transformacja suma jest równa sumie transformowanych.

Dwoistość

F [s_N] → (1/n) s_-K; Jeśli dyskretna transformacja Fouriera zostanie wycofana w wyrażenie już przekształcone, uzyskano to samo wyrażenie, wspinając się w n odwróconym w odniesieniu do osi pionowej.

Skręt

Goniąc podobne cele, które w przekształceniu Laplace'a splot funkcji odnosi się do produktu wśród transformacji Fouriera. Splot dotyczy również dyskretnych czasów i jest odpowiedzialny za wiele nowoczesnych procedur.

X_N * R_N → F [x_N] .F [r_N]; Transformacja splotu jest równa iloczynowi transformowanych.

X_N . R_N→ F [x_N] * F [r_N]; Transformacja produktu jest równa splotowi transformowanych.

Przemieszczenie

X_N-M → F [x_k] e ^{-I (2π/n) km} ; Jeżeli sukcesja jest opóźniona w próbkach M, jej wpływ na dyskretną transformatę będzie modyfikacją kąta zdefiniowanego przez (2π/n) km.

Może ci służyć: dlaczego algebra jest ważna w niektórych codziennych sytuacjach?

Symetria skoniugowany

X_T [-K] = x*_T[k] = x_T [N - k]

Modulacja

W^-nm_N . x [n] ↔ x_T[K - m]

Produkt

x [n] y [n] ↔ (1/n) x_T[k]*i_T[K]

Symetria

X [-n] ↔ x_T[-K] = x*_T[K]

Sprzężony

x*[n] ↔ x*_T[-K]

Równanie Parseval 

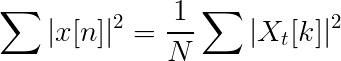
Podobieństwa i różnice z transformacją Fouriera

W odniesieniu do konwencjonalnej transformacyjnej Fouriera, ma kilka podobieństw i różnic. Transformacja Fouriera przekształca sekwencję w ciągłą linię. W ten sposób mówi się, że wynik zmiennej Fouriera jest złożoną funkcją zmiennej rzeczywistej.

Dyskretna transformacja Fouriera, w przeciwieństwie do tego, odbiera dyskretny sygnał i przekształca go w inny dyskretny znak, to znaczy sekwencja.

Jaki jest zastosowanie dyskretnej transformacji Fouriera?

Służą one głównie do znaczących równań, podczas gdy przekształcają wyrażenia uzyskane w elementy mocy. Oznaczanie różnicowych wyrażeń w formach zintegrowalnych wielomianów.

W optymalizacji, modulacji i modelowaniu wyników działa jako standardowe wyrażenie, będąc częstym zasobem inżynierii po kilku pokoleniach.

Źródło: Pixabay

Historia

Ta koncepcja matematyczna została przedstawiona przez Josepha B. Fourier w 1811 r., Opracowując traktat dotyczący Rozprzestrzenianie ciepła. Szybko został przyjęty przez różne oddziały nauki i inżynierii.

Został ustalony jako główne narzędzie robocze w badaniu równań z częściowymi pochodnymi, w porównaniu nawet z relacjami roboczymi między Transformowane i zwykłe równania różniczkowe.

Każda funkcja, którą można przepracować z transformacją Fouriera, musi przedstawić nieważność poza zdefiniowanym parametrem.

Fourier dyskretnie przekształcony i jego odwrotnie

Dyskretna transformacja jest uzyskiwana przez wyrażenie:

Po dyskretnej sekwencji x [n]

Odwrotność dyskretnej transformacji Fouriera jest zdefiniowana przez wyrażenie:

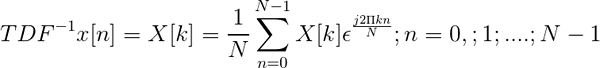Odwrotne TDF

Umożliwia po przekształceniu dyskretnej, zdefiniuj sekwencję w dziedzinie czasu x [n].

Gałganek

Proces parametryzacji odpowiadający dyskretnej transformacji Fouriera leży w Cub. Aby pracować nad transformacją, musimy ograniczyć sekwencję w czasie. W wielu przypadkach, o których mowa, nie mają tych ograniczeń.

Sukcesja, która nie spełnia kryteriów wielkości, która ma zastosowanie do dyskretnej transformacji, można pomnożyć przez funkcję „okna” v [n], określając zachowanie sukcesji w kontrolowanym parametrze.

Może ci służyć: permutacje okrągłe: demonstracja, przykłady, rozstrzygnięte ćwiczenia

X [n] . V [n]

Szerokość widma będzie zależna od szerokości okna. Wraz ze wzrostem szerokości okna obliczone transformowane będzie węższe.

Aplikacje

Obliczanie podstawowego rozwiązania

Dyskretna transformacja Fouriera jest potężnym narzędziem w badaniu dyskretnych sukcesji.

Dyskretna transformacja Fouriera przekształca funkcję zmiennej ciągłej w dyskretną transformację zmienną.

Problem Cauchy'ego w zakresie równania cieplnego przedstawia częste polecenie dyskretnej transformacji Fouriera. Gdzie funkcja jest generowana Ciepło dirichlet lub jądro rdzeniowe, który ma zastosowanie do pobierania próbek wartości w określonym parametrze.

Teoria sygnału

Ogólny powód zastosowania dyskretnej transformacji Fouriera w tej gałęzi wynika głównie z charakterystycznego rozkładu sygnału jako nieskończonego nakładania się sygnałów łatwiejszych do leczenia.

Może to być fala dźwiękowa lub fala elektromagnetyczna, dyskretna transformacja Fouriera wyraża ją w prostym nakładaniu się fali. Ta reprezentacja jest dość częsta w inżynierii elektrycznej.

Seria Fouriera

Są one zdefiniowane serie w kategoriach konsenos i piersi. Służą w celu ułatwienia pracy z ogólnymi funkcjami okresowymi. Po zastosowaniu są częścią technik rozdzielczości częściowych i zwykłych równań różniczkowych.

Serie Fouriera są jeszcze bardziej ogólne niż seria Taylora, ponieważ opracowują okresowe funkcje nieciągłe, które nie mają reprezentacji w serii Taylor.

Inne formy serii Fourier

Analityczne zrozumienie transformacji Fouriera jest to ważne.

-Seria Fouriera w funkcji okresu 2L:

Wiele razy konieczne jest dostosowanie struktury serii Fouriera, do funkcji okresowych, których okres wynosi p = 2l> 0 w przedziale [-L, L].

-Serie Fourier w funkcjach równych i nieparzystnych

Rozważa się interwał [-π, π], który oferuje zalety podczas korzystania z symetrycznych cech funkcji.

Może ci służyć: Zestaw skończony: właściwości, przykłady, rozwiązane ćwiczenia

Jeśli F jest momentem obrotowym, seria Fouriera jest ustanowiona jako seria cosenos.

Jeśli f jest dziwne, seria Fouriera jest ustanowiona jako seria piersi.

-Złożone notacja z serii Fourier

Jeśli masz funkcję F (t), która spełnia wszystkie wymagania serii Fouriera, można ją oznaczyć w przedziale [-t, t] za pomocą złożonej notacji: 

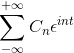
Przykłady

Jeśli chodzi o obliczenia podstawowego rozwiązania, przedstawiono następujące przykłady:

Równanie Laplace'a

Równanie cieplne

Równanie Schrödingera

Równanie fali

Z drugiej strony istnieją przykłady zastosowania dyskretnej transformacji Fouriera w dziedzinie teorii sygnału:

-Problemy z identyfikacją systemu. Ustanowiony F i G

-Problem z spójnością sygnału wyjściowego

-Problemy z filtrowaniem sygnału

Ćwiczenia

Ćwiczenie 1

Obliczyć dyskretną transformację Fouriera dla następującej sukcesji.

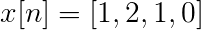
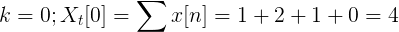
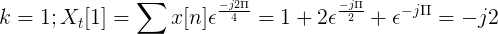
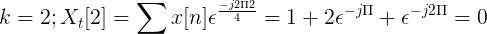
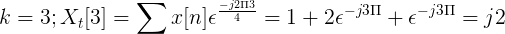
X [n] TDF można zdefiniować jako:

X_T[k] = 4, -J2, 0, j2 dla k = 0, 1, 2, 3

Ćwiczenie 2

Wymagane jest określenie algorytmu cyfrowego sygnał widmowy zdefiniowany przez wyrażenie x (t) = e^-T. Gdzie maksymalna częstotliwość żądająca współczynnika wynosi f_M= 1 Hz. Harmoniczna odpowiada F = 0.3 Hz. Błąd jest ograniczony do mniej niż 5%. Oblicz F_S , D i n.

Biorąc pod uwagę twierdzenie o próbkowaniu F_S = 2f_M = 2 Hz

Rozdzielczość częstotliwości F₀ = 0.1 Hz, gdzie uzyskuje się d = 1/0,1 = 10s

0.3 Hz to częstotliwość odpowiadająca wskaźnikowi k = 3, gdzie n = 3 × 8 = 24 próbki. Wskazując to F_S = N/d = 24/10 = 2.4> 2

Ponieważ celem jest osiągnięcie najmniejszej możliwej wartości dla n, następujące wartości można uznać za rozwiązanie:

F₀ = 0.3 Hz

D = 1/0.3 = 3.33s

K = 1

N = 1 × 8 = 8

Bibliografia

1. Opanowanie dyskretnej transformacji Fouriera w jednym, dwóch lub kilku wymiarach: pułapki i artefakty. Izaak Amidor. Springer Science & Business Media, 19 lipca. 2013
2. DFT: Podręcznik właścicieli dyskretnej transformacji Fouriera. William L. Briggs, Van Emden Henson. Siam, 1 stycznia. 1995
3. Cyfrowe przetwarzanie sygnału: teoria i praktyka. D. Sundararajan. World Scientific, 2003
4. Transformacje i szybkie algorytmy do analizy sygnału i reprezentacji. Guoan Bi, Yonghong Zeng. Springer Science & Business Media, 6 grudnia. 2012
5. Dyskretne i ciągłe transformacje Fouriera: analiza, aplikacje i szybkie algorytmy. Eleanor Chu. CRC Press, 19. 2008