Właściwości transformacji Fouriera, aplikacje, przykłady

Transformacja Fouriera Jest to metoda analitycznej adekwatności zorientowanej na zintegrowalne funkcje należące do rodziny tKompleksowe ransformowane. Składa się z redefinicji funkcji F (t) pod względem cos (t) i sen (t).

Tożsamość trygonometryczna tych funkcji, wraz z ich cechami wyprowadzania i antyderywacyjnymi, służą do zdefiniowania transformacji Fouriera poprzez następującą złożoną funkcję:

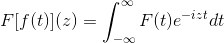
Co jest spełnione, gdy wyrażenie ma sens, to znaczy, gdy niewłaściwa całka jest zbieżna. Algebraicznie mówi się, że transformacja Fouriera jest liniowym homeomorfizmem.

Każda funkcja, którą można przepracować z transformacją Fouriera, musi przedstawić nieważność poza zdefiniowanym parametrem.

[TOC]

Nieruchomości

Źródło: Pexels

Transformacja Fouriera spełnia następujące właściwości:

Istnienie

Aby zweryfikować istnienie transformacji Fouriera w funkcję F (t) zdefiniowaną w Royals R, Należy spełnić następujące 2 aksjomaty:

1. f (t) jest ciągłe na kawałki dla wszystkiego R
2. f (t) jest zintegrowany z R

Liniowość transformacji Fouriera

Niech m (t) i n (t) dwie funkcje z określonymi fanomami, z stałymi A i B dowolne.

F [a m (t) + b n (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)

Który polega również na liniowości całki tej samej nazwy.

Fourier przekształcił się z pochodnej

Masz funkcję F  który jest ciągły i integralny we wszystkich reais, gdzie:

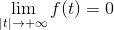
I pochodna F (f ') Jest ciągły i zdefiniowany na kawałki we wszystkim R

Transformacja Fouriera pochodnej jest definiowana przez integrację przez części, przez następujące wyrażenie:

F [f '(t)] (z) = izF [f (t)] (z)

W pochodnych wyższych rzędów będzie stosowany w sposób homologiczny, gdzie dla wszystkich n 1 musisz:

F [F ^N'(t)] (z) = (iz)^NF [f (t)] (z)

Różnicowanie transformacji Fouriera

Masz funkcję F  który jest ciągły i integralny we wszystkich reais, gdzie:

I (D/Dz)F [f (t)] (z) = F  [T .  f (t)] (z)

Fourier przekształcił się z tłumaczenia

Dla wszystkich θ który należy do zestawu i T To należy do zestawu s ', musisz:

F [ τ_Do θ] =  I^-Iyy F [[[ θ]                                 F [ τ_DoT ] =  I^-Iax  F [[[ T]   

Z  τ_Do  Praca jako operator tłumaczeń w wektorze.

Tłumaczenie transformacji Fouriera

Dla wszystkich θ który należy do zestawu i T To należy do zestawu s ', musisz:

τ_Do F [θ] =  F [I^-Iax.θ]                                τ_Do F [t ] =  F [I^-Iyy . T]

Może ci służyć: Hypercubo: Definicja, wymiary, współrzędne, rozwinięte

Dla wszystkich Do który należy do R

Transformacja Fouriera grupy skali

Dla wszystkich θ który należy do zestawu s. T który należy do zestawu S '

λ należeć do R - 0  Musisz:

F [θ (λx)] = (1 / | λ |) F [θ] (I/λ)                 

F [T (λx)] = (1 / | λ |) F [T] (i/λ)

Tak F Jest to funkcja ciągła i czysto integralna, w której A> 0. Więc:

F [f (at)] (z) =   (1/a) F [f (t)] (z/a) 

Aby zademonstrować ten wynik, możemy kontynuować zmianę zmiennej.

Gdy t → + następnie s = at → + ∞

Gdy t → - następnie s = at → - ∞

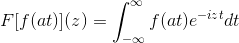
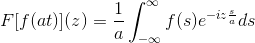
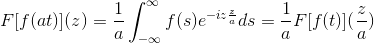
Symetria

Aby zbadać symetrię transformaty Fouriera.

Masz θ i δ, które należą S. Stamtąd można wywnioskować, że:

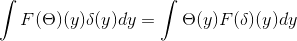
Uzyskanie

1 / (2π)^D  F [θ ], F [δ] Tożsamość Parseval

1 / (2π)^D/2  || F [θ ] ||_L²_R^D     Formuła Plancherel

Fourier przekształcił się z produktu w splot

Goniąc podobne cele, które w przekształceniu Laplace'a splot funkcji odnosi się do produktu wśród transformacji Fouriera.

Ma F i G jako 2 funkcje ograniczone, zdefiniowane i całkowicie zintegrowane:

F (f *g) = f (f) . F (g)

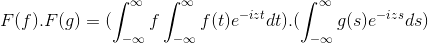
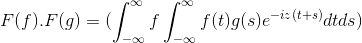
Następnie podczas zmiany zmiennej

t + s = x; Podwójna całka podwójna jest kontynuowana

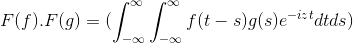
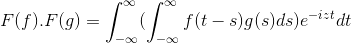
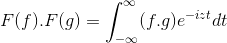
F (f) . F (g) = f (f . G)

Ciągłość i spadek nieskończoności

Dla wszystkich θ należy do R, F [ θ] jest zgodne z kryteriami funkcji ciągłej ograniczonej w R^D.

Również F [ θ] (y) → 0 in c si | y | → ∞

Historia

Ta koncepcja matematyczna została przedstawiona przez Josepha B. Fourier w 1811 roku podczas opracowywania traktatu dotyczącej Rozprzestrzenianie ciepła. Szybko został przyjęty przez różne oddziały nauki i inżynierii.

Został ustalony jako główne narzędzie robocze w badaniu równań z częściowymi pochodnymi, w porównaniu nawet z relacjami roboczymi między Transformowane i zwykłe równania różniczkowe.

Po co Fourier Transform?

Służy głównie do znaczących równań, jednocześnie przekształcając wyrażenia uzyskane w elementy mocy, które oznaczają wyrażenia różnicowe w postaci zintegrowanych wielomianów.

W optymalizacji, modulacji i modelowaniu wyników działa jako standardowe wyrażenie, będąc częstym zasobem inżynierii po kilku pokoleniach.

Seria Fouriera

Są one zdefiniowanymi seriami pod względem konsendy i piersi; Służą w celu ułatwienia pracy z ogólnymi funkcjami okresowymi. Po zastosowaniu są częścią technik rozdzielczości częściowych i zwykłych równań różniczkowych.

Może ci służyć: prawdziwa funkcja zmiennej i jej reprezentacji graficznej

Serie Fouriera są jeszcze bardziej ogólne niż seria Taylora, ponieważ opracowują okresowe funkcje nieciągłe, które nie mają reprezentacji w serii Taylor.

Inne formy serii Fourier

Analityczne zrozumienie transformacji Fouriera jest to ważne.

-Seria Fouriera w funkcji okresu 2L

Wiele razy konieczne jest dostosowanie struktury serii Fouriera, do funkcji okresowych, których okres wynosi p = 2l> 0 w przedziale [-L, L].

-Serie Fourier w funkcjach równych i nieparzystnych

Rozważa się interwał [-π, π], który oferuje zalety podczas korzystania z symetrycznych cech funkcji.

Jeśli F jest momentem obrotowym, seria Fouriera jest ustanowiona jako seria cosenos.

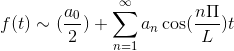
Jeśli f jest dziwne, seria Fouriera jest ustanowiona jako seria piersi.

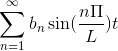
-Złożone notacja z serii Fourier

Jeśli masz funkcję F (t), która spełnia wszystkie rozwinięte wymagania serii Fouriera, można ją oznaczyć w przedziale [-T, t] za pomocą złożonej notacji:

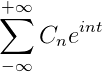
Aplikacje

Źródło: Pexels

Obliczanie podstawowego rozwiązania

Transformacja Fouriera jest potężnym narzędziem w badaniu częściowych równań różniczkowych typu liniowego o stałych współczynnikach. Zastosuj się o funkcje z domenami, które nie są ograniczone równo.

Podobnie jak transformacja Laplace'a, transformacja Fouriera przekształca funkcję częściowych pochodnych, w zwykłe równanie różniczkowe znacznie łatwiejsze w obsłudze.

Problem Cauchy'ego dla równania cieplnego przedstawia częste pole zastosowania transformacji Fouriera, w której funkcja jest generowana Ciepło dirichlet lub jądro rdzeniowe.

Jeśli chodzi o obliczenia podstawowego rozwiązania, przedstawiono następujące przypadki, w których często można znaleźć transformację Fouriera:

-Równanie Laplace'a

-Równanie cieplne

-Równanie Schrödingera

-Równanie fali

Teoria sygnału

Ogólny powód zastosowania transformacji Fouriera w tej gałęzi jest głównie z charakterystycznego rozkładu sygnału jako nieskończonego nakładania się łatwiejszych sygnałów.

Może to być fala dźwiękowa lub fala elektromagnetyczna, transformacja Fouriera wyraża ją w prostych falach. Ta reprezentacja jest dość częsta w inżynierii elektrycznej.

Może ci służyć: linia pionowa

Z drugiej strony są przykładami zastosowania transformacji Fouriera w polu teorii sygnału:

-Problemy z identyfikacją systemu. Ustanowiony F i G

-Problem z spójnością sygnału wyjściowego

-Problemy z filtrowaniem sygnału

Przykłady

Przykład 1

Zdefiniuj transformację Fouriera dla następującego wyrażenia:

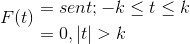
Możemy również reprezentować to w następujący sposób:

F (t) = Sin (t) [h_{(T + k)} - H_{(T - k)} ]

Zdefiniowano prostokątny impuls:

P (t) = h_{(T + k)} - H_{(T - k)}

Transforma Fouriera jest stosowana do następnego wyrażenia, które przypomina twierdzenie o modulacji.

f (t) = p (t) sin (t)

Gdzie: F [w] = (1/2) I [P (w + 1) - P (w - 1)]

A transformacja Fouriera jest zdefiniowana przez:

F [w] =  (1/2) I [(2/2W+1) Sen (K (w+1)) - (2/2W+1) Sen (K (W-1))]

Przykład 2

Zdefiniuj transformację Fouriera dla wyrażenia:

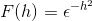Z definicji wyrażamy transformację w następujący sposób

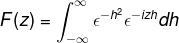
Ponieważ f (h) jest równą funkcją, można to potwierdzić

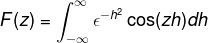Wyrażenie można przepisać w odniesieniu do Z, wyrażenie można przepisać. Ten krok jest znaczący w pracy z równaniami różnicznymi.

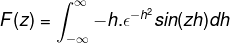
Integracja przez części jest stosowana przez wybór zmiennych i ich różnic w następujący sposób

u = sin (zh) du = z cos (zh) dh

dv = h (e^-H)²                       V = (e^-H)² / 2

Zastąpienie go

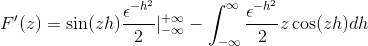
Po ocenie zgodnie z podstawowym twierdzeniem obliczeń

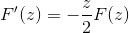
Stosując wcześniejszą wiedzę związaną z równaniami różnicznymi pierwszego rzędu, wyrażenie jest oznaczone jako

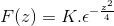
Aby uzyskać K, oceniamy 

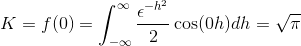
Wreszcie transformacja Fouriera jest zdefiniowana jako

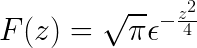
Proponowane ćwiczenia

• Określ transforma Fouriera wyrażenia
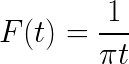
• Rozwiąż następującą niewłaściwą całkę za pomocą równości Pareseval
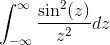
• Uzyskaj transformację wyrażenia w/(1+w²)

Bibliografia

1. Duoandikoetxea Zuazo, J., Analiza Fouriera. Addison- Wesley Iberoamericana, autonomiczny University of Madryt, 1995.
2. Lions, j. L., Analiza matematyczna i numeryczne metody nauki i technologii. Springer-Verlag, 1990.
3. Lieb, e. H., Ziarna Gaussa mają tylko Gaussowskie Maksimery. Wynaleźć. Matematyka. 102, 179-208, 1990.
4. Dym, h., McKean, godz. P., Serie Fouriera i całki. Academic Press, New York, 1972.
5. Schwartz, L., Théorie des Distribution. Wyd. Hermann, Paryż, 1966.