Toroid lub toro dona

Wyjaśniamy, czym jest byk lub byk, jego cechy, objętość, powierzchnia, zastosowania i pokazujemy kilka przykładów

Co to jest toroid?

On Toroid Jest to trójwymiarowe ciało geometryczne w postaci obręczy, pierścienia, pierścienia, pączki lub pączki, stąd nazwa „Toro Dona”, należące do klasy nazywanych obiektów zwanych Solidne rewolucyjne.

Toroid jest generowany przez obracanie zamkniętej płaskiej figury, wokół linii należącej do tej samej płaszczyzny figury, ale nie przechwytuje go, jak pokazano poniżej:

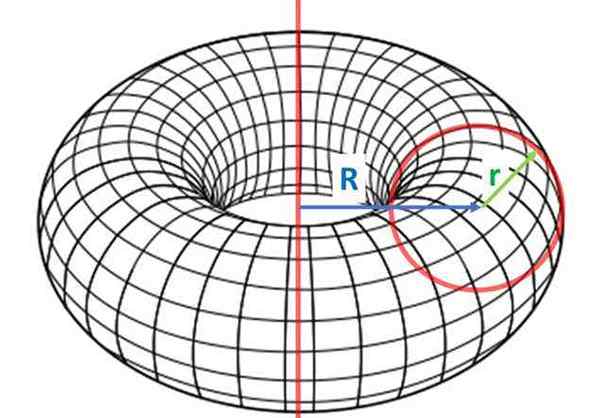
Byk, który jest powierzchnią rewolucji, która jest uzyskiwana przez obracanie zamkniętej płaskiej figury (jako obwód) wokół stałej osi. Źródło: Wikimedia Commons

Główną cechą toroidu jest to, że pomimo tego, że jest zamkniętą powierzchnią, ma otwór. Oznacza to, że dwa punkty jej powierzchni mogą być połączone przez segment poza obiektem.

Kolejną cechą toroidów jest to, że jest to figura trójwymiarowa bez wierzchołków. Ta charakterystyka dzieli go z innymi ciałami objętościowymi, takimi jak kula, ale chociaż kula jest wypukłą powierzchnią, byk jest jednocześnie wklęsły i wypukły.

Wśród byków, byk Jest najczęstszy i jest uzyskiwany z obrotu koła radiowego R, Jeśli chodzi o oś odległości R pierwszego. Radio R (małe litery) jest znane jako mniejszy promień, a R (kapitał) jest największym promieniem.

Objętość toroidów

Byk jest generowany przez obracanie zamkniętej płaskiej postaci o powierzchni DO wokół osi obrotu, która go nie przecięła. Oznaczanie przez R Odległość od osi do środka ciężkiego płaskiego figury objętość byka rewolucyjnego wynosi:

Może ci służyć: odwrotne funkcje trygonometryczne: wartość, pochodne, przykłady, ćwiczenia

V = 2πr⋅ a 

Ten wynik jest uzyskiwany podczas stosowania Twierdzenie Pappus Dla objętości substancji stałej rewolucji, która stwierdza, że ​​objętość dowolnej rewolucji stałej uzyskuje się poprzez pomnożenie obszaru liczby, która jest zepsuta przez obwód obwodu utworzony przez obrót środka ciężkości (lub środek ciężkości ) z obraconej figury, wokół osi obrotu.

Objętość byka

Byk to toroid generowany przez koło radiowe R. Jeśli odległość osi obrotu od środka obróconego okręgu wynosi r, konieczne jest objętość byka jest:

V = (2πr) ⋅ (πr²) = 2π²R³

Powierzchnia byka

Być po prostu pokrewną płaską figurą DO i kontur L. Jeśli taka figura jest obracana wokół osi zawartej w tej samej płaszczyźnie figury, ale to nie przekracza, wówczas wygenerowana powierzchnia jest bykiem powierzchniowym:

S = 2πr⋅ l

Odległość od osi do środka grawitacji lub środka ciężkości, z figury generatrix.

Ten wynik jest konsekwencją Twierdzenie Pappus Dla powierzchni rewolucji stałej.

Powierzchnia byka

Okrągły krzyżowy byk radia R (małe litery) i burmistrz radiowy R (Ojczyka) to szczególny byk o nazwie Toro.

Jak kontur LUS 2πr, Wtedy obszar powierzchni wspomnianego byka to:

S = (2πr) ⋅ (2πr) = (4π²) (R⋅ R)

Aplikacje toroidalne

Ze względu na charakterystykę geometryczną byk ma niezliczone praktyczne i kulturowe zastosowania. Na początek obręcze lub pierścienie to części toroidalne, które mają różne zastosowania:

Może ci służyć: minimalne kwadraty

Kulturalny

• Zastosowanie ozdobne lub kosmetyczne, gdy pierścień jest umieszczany na palcu lub po umieszczeniu piercingu do ucha.
• W nosie wołów umieszcza się obręcz, który służy do powiązania i kontrolowania.
• Kiedy pierścień lub pierścień są umieszczone w lewej ręce na palcu serdecznym, ma on konotację społeczną, która pochodzi z czasów starożytnych Greków i oznacza zaangażowanie, wierność i małżeństwo z parą, która przenosi obręcz w tym samym sposób i materiał.

W mechanice

Poza kontekstem ozdobnym, kosmetycznym i kulturowym, byk ma wiele praktycznych zastosowań. W mechanice toroid jest używany jako pierścień retencyjny łożyska w końcówce osi pojazdu. 

Również łożyska pojazdów silnikowych są składane przez jedną lub dwa obręcze w postaci byka z różnymi formami przekroju, na których toczą cylindry lub kule, w celu zmniejszenia tarcia w osiach.

W elektryczności

W zastosowaniach elektrycznych toroid ma również ogromne znaczenie, ponieważ jądra ferromagnetyczne induktorów, elektromagery i transformatorów często mają kształt byka, a na nich kabel w postaci cewki.

Tokamak

Istnieje rodzaj kontrolowanego reaktora fuzyjnego w postaci toroidu lub pączku nazywanego jego rosyjską nazwą: TOkamak. W tego typu reaktora fuzyjnego jądrowego pojemnik i cewki wytwarzające pole magnetyczne ograniczenia osocza mają kształt toroidalny lub usposobienie.

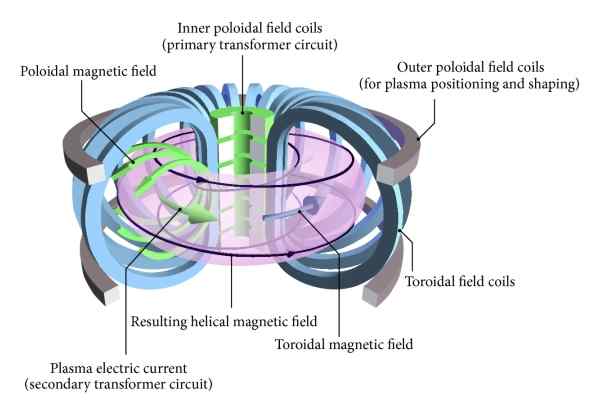Rysunek schematycznie pokazuje kontrolowany reaktor fuzji jądrowej w formie toroidalnej znanej jako „Tokamak”. W tego rodzaju reaktora zarówno osocza, cewki, jak i pole magnetyczne uwięzienia mają konfigurację toroidalną. Źródło: Wikimedia Commons

Przykłady

Powierzchnia kwadratowego byka odcinka (według wzoru)

W tym przykładzie rozdział kwadratowy jest uważany za pokazany na poniższym rysunku:

Może ci służyć: Scaleno Triangle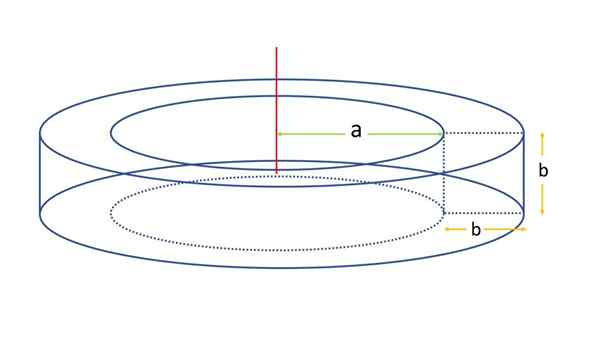 Toroidowa sekcja kwadratowa. Źródło: f. Zapata

Powierzchnia zostanie określona za pomocą wzoru powierzchni dla ogólnego byka. W tym celu konieczne jest znanie odległości osi obrotu od środka centroidu kwadratu, który za pomocą poprzedniej nomenklatury wynosi R:

R = a + b/2

Konieczne jest również znanie obwodu L figury generatrix, która jak w tym przypadku jest kwadratem z boku B, Jego kontur będzie długi:

L = 4⋅B

Następnie stosuje się formułę powierzchni byka:

S = 2πr⋅l

Zastąpienie R i L dla odpowiednich wyrażeń, w zależności od miar A i B kwadratowego byka to:

S = 2π (A + B/2) ⋅4⋅B = 8π (A + B/2) ⋅B

Kwadratowa powierzchnia toroidowa (suma jej twarzy)

Kwadratowy byk poprzedniej figury składa się z czterech twarzy: górna i dolna to płaskie pierścienie, a wnętrze i zewnętrzne są cylindryczne.

Biorąc to pod uwagę, można obliczyć jego powierzchnię, dodając obszar jego czterech twarzy.

Górne i dolne twarze mają powierzchnię równą powierzchni zewnętrznego koła o promieniu (A+B) mniej niż wewnętrzny krąg radia Do, które w rezultacie:

S_S= S_Siema= π [(A+B)² - B²] = π⋅ [a²+ 2AB]

Wewnętrzna cylindryczna twarz ma obszar:

S₁= 2πab

A zewnętrzna cylindryczna twarz ma obszar:

S₂= 2π (a+b) b = 2πab+2πb²

Tak, aby całkowita powierzchnia toroidów była sumą_S+S_Siema+S₁+S₂:

A = 2π⋅ [a²+ 2Ab]+2πab+2πab+2πb².