Przykłady paraboliczne, wzory i równania, przykłady

On Strzał paraboliczny Polega na rzucaniu obiektu lub pocisku pod pewnym kątem i pozwalając mu poruszać się pod działaniem grawitacji. Jeśli opór powietrza nie zostanie uwzględniony, obiekt, niezależnie od jego natury, będzie zgodny z trajektorią w postaci paraboli.

Jest to codzienny ruch, ponieważ wśród najpopularniejszych sportów są te, w których piłki lub piłki są rzucane ręcznie, z stopą, albo z instrumentem, na przykład rakiety lub nietoperza.

Rysunek 1. Strumień wodny ze źródła ozdobnego jest zgodny z trajektorią paraboliczną. Źródło: Wikimedia Commons. Zátonyi Sandor (IFJ.), Fizped/cc by-sa (https: // creativeCommons.Org/licencje/by-sa/3.0)

Do badania strzał paraboliczny jest podzielony na dwa nakładające się ruchy: jeden poziomy bez przyspieszenia, a druga pionowa z ciągłym przyspieszeniem, co jest grawitacją. Oba ruchy mają początkową prędkość.

Powiedzmy, że ruch poziome. Każdy z tych ruchów jest niezależny od drugiego.

W związku z faktem, że określenie pozycji pocisku jest głównymi celami, konieczne jest wybranie odpowiedniego systemu odniesienia. Szczegóły są następne.

[TOC]

Formuły i równania strzału parabolicznego

Załóżmy, że obiekt jest wyrzucany z kątem α w odniesieniu do prędkości poziomej i początkowej v_albo jak pokazano na poniższym rysunku po lewej stronie. Strzał paraboliczny to ruch, który odbywa się w samolocie Xy I w takim przypadku początkowa prędkość rozkłada się w ten sposób:

v_wół = v_albo cos α

v_Oy = v_albo sin α

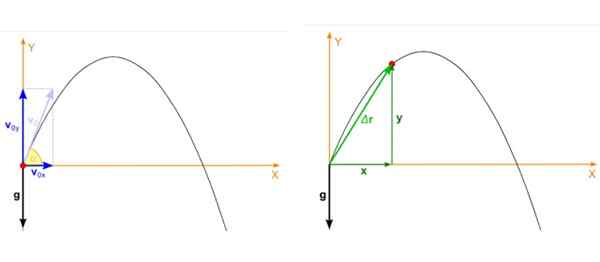Rysunek 2. Po lewej stronie początkowa prędkość pocisku i po prawej stronie pozycja w dowolnym momencie uruchomienia. Źródło: Wikimedia Commons. Zátonyi Sandor, (IFJ.) Fizped/cc by-sa (https: // creativeCommons.Org/licencje/by-sa/3.0).

Pozycja pocisku, która jest czerwonym punktem na ryc. 2, prawy obraz, ma również dwa elementy, które zależą od czasu, jeden w X A drugi w I. Pozycja jest wektorem oznaczonym jako R a jego jednostki są długie.

Może ci służyć: izomeria

Na rysunku początkowa pozycja pocisku pokrywa się z pochodzeniem układu współrzędnych, a zatem x_albo = 0 i_albo = 0. Nie zawsze tak jest, pochodzenie można wybrać w dowolnym miejscu, ale ten wybór bardzo upraszcza obliczenia.

Jeśli chodzi o dwa ruchy w X i Y, są to:

-X (t): Jest to jednolity ruch prostoliniowy.

-i (t): odpowiada jednolicie przyspieszonym ruchu prostoliniowym z g = 9.8 m/s² i wskazując pionowo.

W formie matematycznej:

x (t) = v_albo cos α.T

i (t) = v_albo .sin α.T - ½G.T²

Wektor pozycji pozostaje:

R (t) = [v_albo cos α.T]Siema + [v_albo .sin α.T - ½G.T²] J

W tych równaniach uważny czytelnik zauważy, że znak minus jest spowodowany faktem, że nasilenie wskazuje na ziemię, sens wybrany jako negatywny, podczas gdy w górę jest uznany za pozytywny.

Ponieważ prędkość jest pierwsza pochodząca z pozycji, wystarczy wyprowadzić R (t) dotyczące czasu i uzyskania:

v (t) = v_albo cos α Siema + (v_albo .sin α - GT) J

Wreszcie przyspieszenie jest wyrażane wektorowo jako:

Do (t) = -G J

- Trajektoria, maksymalna wysokość, maksymalny czas i zasięg poziomego

Trajektoria

Aby znaleźć jawne równanie trajektorii, które jest krzywą (x), musisz wyeliminować parametr czasu, usuwając w równaniu dla x (t) i zastępując w y (t). Uproszczenie jest nieco pracochłonne, ale ostatecznie zostaje uzyskane:

Maksymalna wysokość

Maksymalna wysokość występuje, kiedy v_I = 0. Wiedząc, że istnieje następny związek między pozycją a kwadratem prędkości:

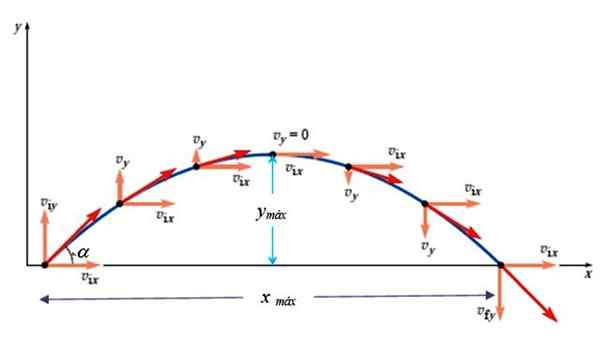Rysunek 3. Prędkość w parabolicznym ujęciu. Źródło: Giambattista, a. Fizyka.

v_I² = v_Oy ²- 2Gy

Czyn v_I = 0 Właśnie wtedy, gdy sięga na maksymalnej wysokości:

0 = v_Oy ²- 2 g.I_Max → i_Max = v_Oy ²/2 g

Z:

Może ci służyć: przyspieszenie dośrodkowe: definicja, wzory, obliczenia, ćwiczenia

v_Oy = v_albo Senα

Maksymalny czas

Maksymalny czas to czas, który obiekt potrzebuje do osiągnięcia i_Max. Aby go obliczyć, jest używany:

v_I = v_albo .sin α - Gt

Wiedząc to v_I Jest to zrobione 0, kiedy t = t_Max, wynik:

v_albo .sin α - G.T_Max = 0

T_Max = v_Oy /G

Maksymalny zasięg poziomego i czas lotu

Zakres jest bardzo ważny, ponieważ wskazuje, gdzie obiekt spadnie. Więc będziemy wiedzieć, czy daje to na biało. Aby go znaleźć, potrzebujemy czasu lotu, całkowitego czasu lub t_v.

Z poprzedniej ilustracji łatwo jest to stwierdzić T_v = 2.T_Max. Ale uwaga jest prawdziwa tylko wtedy, gdy uruchomienie jest na poziomie, to znaczy wysokość punktu początkowego jest taka sama jak wysokość przyjazdu. W przeciwnym razie czas rozwiązuje równanie drugiego stopnia, które wynika z wymiany pozycji końcowej I_finał:

I_finał = v_albo .sin α.T_v - ½G.T_v²

W każdym razie maksymalny poziom poziomy to:

X_Max = v_wół. T_v

Przykłady strzelania parabolicznego

Strzał paraboliczny jest częścią ruchu ludzi i zwierząt. Również prawie wszystkie sport i gry, w których grawitacja interweniuje. Na przykład:

Strzelanie paraboliczne w ludzkich działaniach

-Kamień rzucony przez katapulta.

-Kopnięcie bramka bramkarza.

-Piłka, która rzuca miotacz.

-Strzała, która wychodzi z łuku.

-Wszelki rodzajów skoków

-Rzuć kamień.

-Każda broń rzucająca.

Rysunek 4. Kamień rzucony przez katapult i Patey Ball w polu końcowym są przykładami parabolicznych ujęć. Źródło: Wikimedia Commons.

Strzał paraboliczny w naturze

-Woda wyrastająca z naturalnych lub sztucznych odrzutowców, takich jak źródło.

-Kamienie i lawa wyrastają z wulkanu.

-Piłka, która odbija się na chodniku lub kamień, który robi to na wodzie.

-Wszystkie rodzaje zwierząt, które skakają: kangur, delfiny, gazele, kocie, żaby, króliki lub owady, aby wymienić kilka.

Może ci służyć: moc mechaniczna: co to jest, aplikacje, przykładyRysunek 5. Impala jest w stanie skakać do 3 m. Źródło: Wikimedia Commons. Arturo de Frias Marques/cc by-S (https: // creativeCommons.Org/licencje/by-sa/3.0).

Ćwiczenia

Plagryspper tworzący kąt 55 ° z poziomym i ląduje na 0.80 metrów później. Znajdować:

a) maksymalna wysokość osiągnięta.

b) Jeśli skoczę z tą samą prędkością początkową, ale tworząc kąt 45º, czy wzrósłby wyżej?

c) Co można powiedzieć o maksymalnym zasięgu poziomym dla tego kąta?

Rozwiązanie

Gdy dane dostarczone przez problem nie zawierają początkowej prędkości v_albo Obliczenia są nieco bardziej pracochłonne, ale z znanych równań można wywnioskować nowe wyrażenie. Zaczynając od:

X_Max = v_wół . T_lot = v_albo.cos α. T_v

Kiedy wyląduje później, wysokość znów wynosi 0, to:

v_albo .sin α.T_v - ½G.T_v²= 0

Jak T_v Jest to powszechny czynnik, jest uproszczony:

v_albo .sin α - ½G.T_v= 0

Możemy wyczyścić t_v Z pierwszego równania:

T_v = x_Max / v_albo.cos α

I wymień w drugim:

v_albo .sin α - (½G.X_Max / v_albo.cos α) = 0

Mnożąc wszystkie warunki przez v_albo.cos αWyrażenie się nie zmienia, a mianownik znika:

(v_albo .sin α.) (v_albo.cos α) - ½G.X_Max = 0

v_albo² sin α. cos α = ½g.X_Max

Można już wyczyścić v_albo lub również zastąpić następującą tożsamość:

Sen 2α = 2 Sen α. cos α → v_albo² Sen 2α = G.X_Max

Jest wyliczone v_albo²:

v_albo² = g.X_Max / Sen 2α = (9.8 x 0.8 / Sen 110) m²/S² = 8.34 m²/S²

I wreszcie maksymalna wysokość:

I_Max= v_Oy ²/2G = (8.34 x sen² 55)/(2 x 9.8) M = 0.286 m = 28.6 cm

Rozwiązanie b

Homarowi udaje się zachować tę samą prędkość poziomą, ale gdy kąt maleje:

I_Max= v_Oy ²/2G = (8.34 x sen² 45)/(2 x 9.8) M = 0.213 m = 21.3 cm

Osiąga mniejszą wysokość.

Rozwiązanie c

Maksymalny poziom poziomy to:

X_Max = v_albo² Sen 2a / G

Gdy kąt zmienia się, zakres poziomy również zmienia się:

X_Max = 8.3. 4 Sen 90 / 9.8  M = 0.851 m = 85.1 cm

Skok jest teraz dłuższy. Czytnik może sprawdzić, czy jest maksymalny dla kąta 45 °:

sin 2α = sin 90 = 1.

Bibliografia

1. Figueroa, zm. 2005. Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. Pod redakcją Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fizyka. Druga edycja. McGraw Hill.
3. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
4. Resnick, r. 1999. Fizyczny. Tom. 1. Wydanie trzecie. po hiszpańsku. Continental Editorial Company S.DO. c.V.
5. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1.