Rodzaje całek
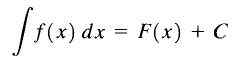
- 3936
- 1016
- Herbert Wróblewski
Rodzaje całek że jesteśmy w obliczeniach, to całki nieokreślone i zdefiniowane całki. Chociaż zdefiniowane całki mają o wiele więcej aplikacji niż całki nieokreślone, najpierw należy nauczyć się rozwiązywać nieokreślone całki.
Jednym z najbardziej atrakcyjnych zastosowań zdefiniowanych całek jest obliczenie objętości stałej rewolucji. Oba typy całek mają te same właściwości liniowości, a także techniki integracji nie zależą od rodzaju całki.
Ale pomimo tego, że jest bardzo podobna, istnieje główna różnica; W pierwszym typie całki wynik jest funkcją (co nie jest specyficzne), podczas gdy w drugim typu wynik jest liczbą.
Podstawowe typy całek
Świat integralów jest bardzo szeroki, ale w tym możemy rozróżnić dwa podstawowe rodzaje całek, które mają duże zastosowanie w życiu codziennym.
1- Integrals nieokreślony
Jeśli f '(x) = f (x) dla wszystkich x w domenie f, mówimy, że f (x) jest antykiwującym, prymitywnym lub całkową f (x).
Z drugiej strony zauważmy, że (f (x)+c) '= f' (x) = f (x), co implikuje, że całka funkcji nie jest unikalna, ponieważ nadaje różne wartości stałej stałej C Otrzymamy różne antyeksywacje.
Z tego powodu f (x)+c nazywany jest nieokreśloną całką f (x) i c nazywana jest stałą integracji i piszemy ją w następujący sposób:
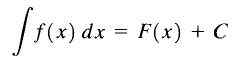 Integral nieokreślony
Integral nieokreślony Jak widzimy, nieokreślona całka funkcji f (x) jest rodziną funkcji.
Na przykład, jeśli chcesz obliczyć nieokreśloną całkę funkcji f (x) = 3x², najpierw należy znaleźć antideriwalność f (x).
Może ci służyć: trójmianŁatwo zauważyć, że f (x) = x³ jest antykiwującym, ponieważ f '(x) = 3x². Dlatego można to stwierdzić
∫f (x) dx = ∫3x²dx = x³+c.
2- Zdefiniowane całki
Niech y = f (x) rzeczywistą funkcję trwa w zamkniętym odstępie [a, b] i będzie f (x) antideriwalność f (x). Nazywa się to zdefiniowaną całką f (x) między limitami a i b do liczby f (b) -f (a) i oznacza następująco:
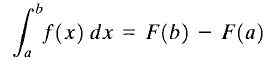 Twierdzenie o obliczeniach podstawowych
Twierdzenie o obliczeniach podstawowych Wzór pokazany powyżej jest lepiej znany jako „podstawowe twierdzenie obliczeń”. Tutaj „A” nazywa się dolną granicą, a „B” nazywa się górną granicą. Jak widać, określona całka funkcji jest liczba.
W takim przypadku, jeśli określona całka F (x) = 3x² zostanie obliczona w przedziale [0,3], zostanie uzyskana liczba.
Aby określić tę liczbę, wybieramy f (x) = x³ jako antyiderivatywne f (x) = 3x². Następnie obliczamy f (3) -f (0), co w wyniku wyrzuca nas 27-0 = 27. Podsumowując, zdefiniowana całka F (x) w przedziale [0,3] wynosi 27.
Można zauważyć, że jeśli g (x) = x3+3, wówczas g (x) jest wybrane, jest antideriwalnością f (x) inną od f (x), ale nie wpływa to na wynik jako g (3) -G (0) = (27+3)-(3) = 27. Z tego powodu w określonych całkach nie pojawia się stała integracji.
Jedną z najbardziej przydatnych zastosowań, jakie ma ten rodzaj całki, jest to, że pozwala obliczyć obszar (objętość) płaskiej figury (rewolucji solidnej), ustanawianie odpowiednich funkcji i ograniczeń integracji (i osi obrotu).
Spośród zdefiniowanych całek możemy znaleźć różne rozszerzenia tego, takie jak linie całkowe, całki powierzchniowe, niewłaściwe całki, wiele całek, między innymi, z bardzo przydatnymi zastosowaniami w nauce i inżynierii.
Może ci służyć: różnica między okrągiem a obwodem (z przykładami)Bibliografia
- Kishan, h. (2005). Rachunek integralny. Atlantic Publishers & Dystrybutorzy.
- Purcell, e. J., Varberg, d., & Rigdon, s. I. (2007). Obliczenie (Dziewiąty ed.). Prentice Hall.

