Miletus takie twierdzenie

Wyjaśniamy pierwsze i drugie twierdzenie takie, z ustalonymi przykładami i ćwiczeniami

Rysunek 1.- Twierdzenie opowieści

Co jest takie?

On takie twierdzenie Od Miletus w rzeczywistości odnosi się do kilku twierdzeń geometrii przypisanych mądrze starożytnych Grecji Thales z Miletu, który żył od 624 do 546 AC w ​​Miletus, obecnej indyka.

Oprócz matematyka i geometru, taki był filozof uznany za jego wielką ostrość. Mówi się, że udało mu się zmierzyć wysokość wielkiej piramidy za pomocą jednego z jej twierdzeń.

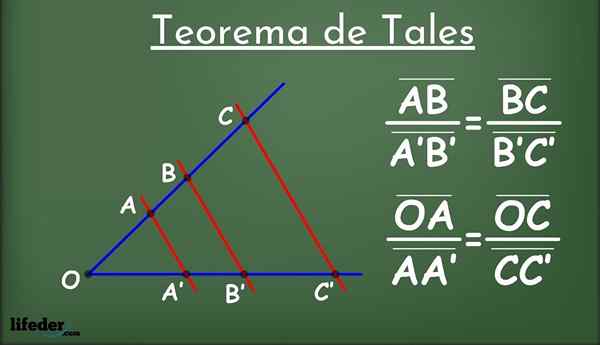
On Pierwsze twierdzenie o takich Odnosi się do segmentów, które grupa równoległych linii określa w dwóch liniach w płaszczyźnie. Segmenty te zachowują stosunek proporcjonalności, co zostanie wkrótce widoczne, co jest rozszerzone na boki dwóch trójkątów, pod warunkiem, że spełnione są pewne warunki.

Twierdzenie to jest niezwykle przydatne w praktyce, ponieważ pozwala określić wysokość bardzo wysokich lub trudnych do dostępu struktur, bez konieczności bezpośrednio ich pomiaru. Właśnie to zrobił opowieści, kiedy mierzył wysokość wielkiej piramidy.

Ze swojej strony Drugie twierdzenie o tym Punkty łącza należące do obwodu z zarejestrowanym w nim trójkątem prostokąta, którego przeciwprostokątna zbiega się z jego średnicą.

Pierwsze twierdzenie o takich

Być dwiema liniami w płaszczyźnie, zwanym L₁ i ja₂ (na niebiesko na ryc. 1) i grupa linii równolegle do siebie (w kolorze czerwonym), które przecinają L₁ i ja₂.

Równoległe linie dzielą linie na segmenty l₁ i ja₂: Ab, a'b ', bc, b'c' i tak dalej. Wśród segmentów ustalono następujący związek proporcjonalności:

Na przykład na tym rysunku miara segmentu „x” jest obliczana przez twierdzenie takiego, ponieważ linie są przecinane przez kilka paraleli, które określają segmenty o znanej długości:

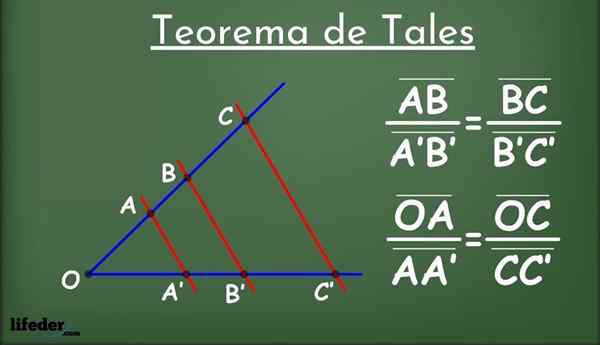
Może ci służyć: wzajemnie wykluczające się wydarzenia: właściwości i przykładyRysunek 2.- Zastosowanie pierwszego takiego twierdzenia do określenia miary segmentu x. Źródło: f. Zapata.

3x = 32

x = 32/3 ≈ 10.7

Takie twierdzenie o podobnych trójkątach

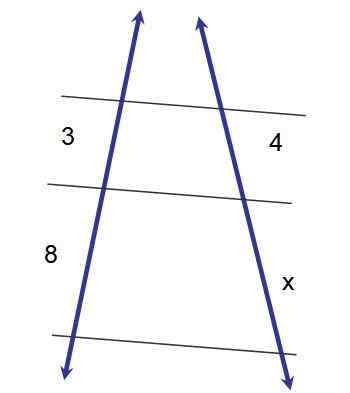
Twierdzenie można rozszerzyć na trójkąty w następujący sposób: Załóżmy, że istnieje trójkąt ABC, na którym segment równoległy jest rysowany na jedną z jego stron. W ten sposób uzyskuje się dwa podobne trójkąty: ABC i DEC, których wewnętrzne kąty są zgodne, to znaczy mają równą miarę.

Rysunek 3.- Dwa trójkąty w pozycji takich, z dwiema równoległymi stronami i wspólnym kątem, są podobne. Źródło: f. Zapata.

Kiedy masz w ten sposób ułożone dwa trójkąty, mówi się, że są one w takiej sytuacji.

Stosunek proporcjonalności między segmentami jest podniesiony w taki sam sposób, jak w przypadku linii równoległych:

Co jest równoważne z tym drugim, między odpowiednimi stronami każdego trójkąta, zwane także homologicznymi stronami:

Każdy z tych ilości jest nazywany Powód podobieństwa. W podobnych trójkątach przyczyna podobieństwa jest równa ilorazu między obwodami a kwadratem współczynnika podobieństwa jest równe ilorazie między obszarami.

Następnie przykład, w którym takie twierdzenie można zastosować do podobnych trójkątów i dowiedzieć się, ile warta jest nieznana strona X.

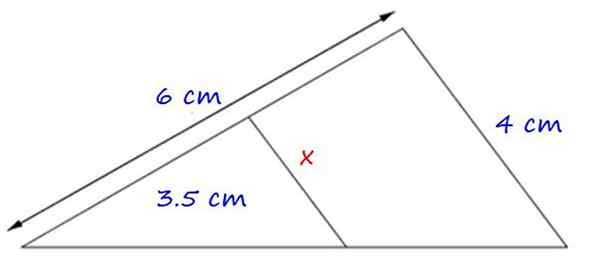Rysunek 4.- Przykład zastosowania pierwszego takiego twierdzenia. Źródło: f. Zapata.

Utworzone trójkąty są podobne, ponieważ mają wspólny kąt, a boki x i 4 cm są równoległe.

Dlatego proporcjonalność między odpowiednimi stronami wynosi:

A wartość x można łatwo usunąć:

x = (4 × 3.5) ÷ 6 cm = 2.3 cm

Drugie twierdzenie o tym

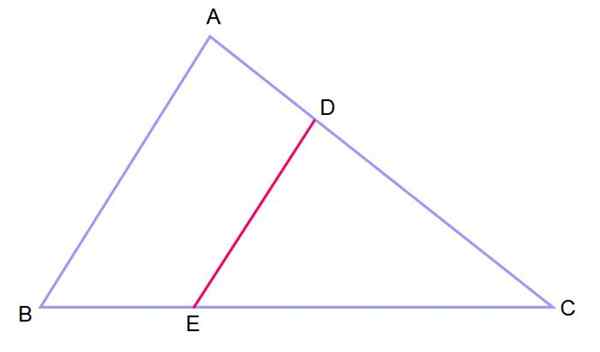
Twierdzenie to odnosi się do trójkąta, którego wierzchołki są punktami należącymi do obwodu, co oznacza, że ​​jest w nim zarejestrowany.

W tym przypadku twierdzenie określa, że ​​za każdym razem, gdy hipotenus odpowiada średnicy obwodu, trójkąt w ten sposób prześledzony jest prostokątem, to znaczy jeden z jego wewnętrznych kątów mierzy 90º, jak pokazano na rycinie 5 do lewej strony.

Może ci służyć: symbolizacja wyrażeń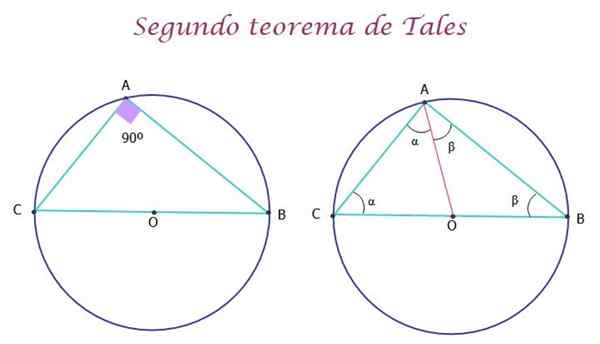Rysunek 5.- Drugim twierdzeniem takich stanów, że trójkąt zarejestrowany w obwodzie jest prostokąt. Źródło: f. Zapata.

Demonstracja drugiego twierdzenia takiego

Demonstracja twierdzenia jest bardzo prosta. Na powyższym rysunku segment AO został narysowany na czerwono, tworząc dwa trójkąty AOC i AOB, które są izoscelesami, ponieważ boki OA, OC i OB są radia o obwodzie, a zatem mierzą to samo.

W ten sposób trójkąty mają dwa równe kąty, które są odpowiednio α i β. Teraz, dla oryginalnego trójkąta ABC, podobnie jak każdy trójkąt, spełniono, że suma miar jego wewnętrznych kątów jest równa 180º, dlatego:

α + (α + β) + β = 180º

Stąd:

2α + 2β = 180º

Dlatego:

2 (α +β) = 180º

α +β = 90º

Co dowodzi, że trójkąt ABC ma wewnętrzny kąt 90º, a zatem jest prawym trójkątem.

Przykład

Na poniższym rysunku trójkąt ABC to izosceles i prostokąt (trójkąt izorektangle), będąc obwodem obwodu równego 25 cm. Ile kosztują segmenty AC i AB?

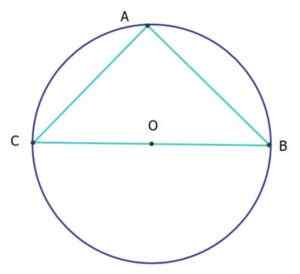
Obwód obwodu jest jego długość L, podana w zależności od jego średnicy D według wzoru:

L = πd

Dlatego średnica, która jest segmentem CB, mierzy:

D = cb = l/ π = 25 cm/ π = 7.96 cm.

Ponieważ trójkąt jest izoscelesem, oznacza to, że jego ostre kąty mierzą 45º. Ponieważ hipotenusa trójkąta jest średnicą obwodu, można zastosować stosunek trygonometryczny 45, na przykład:

Sen 45º = AC/CB

AC = CB × Sin 45º = 7.96 cm × sin 45º = 5.64 cm

Może ci służyć: Twierdzenie Moivre

Strona AB ma tę samą miarę: 5.64 cm, ponieważ trójkąt to izosceles.

Takie aplikacje twierdzenia

Pierwsze takie twierdzenie można wykorzystać do poznania odległości, które nie są łatwo mierzalne. Mówi się, że takie udało się do Egiptu i tam zdeterminował, że wysokość wielkiej piramidy.

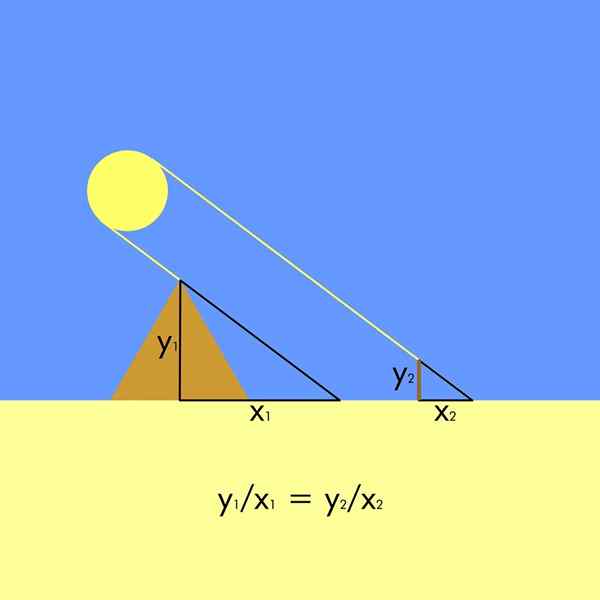
W tym celu było to konieczne. Tak więc powstają dwa podobne trójkąty, ponieważ promienie słoneczne mają równoległe występowanie.

Na rysunku wysokość piramidy jest i₁ A jego cień jest x₁, Podczas gdy wysokość palika jest i₂ (Niektórzy kronikarze twierdzą, że taki używali własnej wysokości), a ich cień jest x₂. Ponieważ trójkąty są podobne, powstaje następujący związek proporcjonalności:

Bardzo łatwo wyczyścić wysokość piramidy i₁:

I₁ = x₁∙ (i₂ ÷ x₂)

Bibliografia

1. Alexander, zm. 2013. Geometria. 5. Wydanie. Cengage Learning.
2. Requena, ur. Takie twierdzenie. Odzyskane z: Universoformulas.com.
3. Sala matematyczna. Tales de Mileto i Wielka Piramida. Pobrano z: salonmatematic.com
4. Materiał dydaktyczny Superprof. Miletus taki. Odzyskane z: Superprof.Jest.
5. Twierdzenie i podobieństwo. Dwa bardzo stare problemy. Odzyskane z: edu.Xunta.Gal.