Twierdzenie o wyjaśnieniach Steiner, aplikacje, ćwiczenia

On Twierdzenie Steinera, znany także jako Twierdzenie o osi równoległej, Pozwala ocenić moment bezwładności przedłużonego ciała, wokół osi, która jest równoległa do drugiego, która przechodzi przez środek masy obiektu.

Został odkryty przez szwajcarską matematykę_Cm moment bezwładności obiektu w odniesieniu do osi, która przechodzi przez jego CM i I Mass Center_z moment bezwładności w odniesieniu do innej równoległej osi do tego.

Rysunek 1. Prostokątne drzwi włączające swoje radości mają chwilę bezwładności, którą można obliczyć, stosując twierdzenie Steinera. Źródło: Pixabay.

Znana odległość D, która oddziela zarówno osie, jak i masę M od omawianego ciała, moment bezwładności w odniesieniu do osi incognito wynosi:

Siema_z = I_Cm + MD²

Moment bezwładności wskazuje, jak łatwo jest obracać obiekt wokół określonej osi. Zależy to nie tylko od ciała ciała, ale od tego, jak jest rozmieszczone. Z tego powodu jest to również znane jako Bezwładność obrotowa, Bycie swoimi jednostkami w międzynarodowym systemie KG . M².

Twierdzenie pokazuje, że moment bezwładności Siema_z Jest zawsze większy niż moment bezwładności Siema_Cm w cenie podanej przez M.D².

[TOC]

Aplikacje

Ponieważ obiekt jest w stanie obracać się wokół wielu osi, a w tabelach zwykle tylko moment bezwładności dotyczącej osi przechodzący przez centroid, twierdzenie Steinera ułatwia obliczenia, gdy musi obracać ciała na osiach, które nie pokrywają się z Ten.

Może ci służyć: ruch prostoliniowy: cechy, typy i przykłady

Na przykład drzwi zwykle nie obraca się wokół osi, która przechodzi przez jej środek masy, ale w odniesieniu do osi bocznej, w której zawiasy przylegają.

Kiedy znając moment bezwładności, możliwe jest obliczenie energii kinetycznej związanej z obrotem na tej osi. Tak K jest energią kinetyczną, Siema moment bezwładności wokół danej osi i Ω Prędkość kątowa jest spełniona, że:

K = ½ i.Ω²

To równanie jest bardzo podobne do bardzo znanej wzoru energii kinetycznej dla obiektu masowego M poruszanie się z prędkością v:  K = ½ m.v². I jest to, że moment bezwładności lub bezwładności obrotowej Siema odgrywa w rotacji taką samą rolą co ciasto M W tłumaczeniu.

Demonstracja twierdzenia Steinera

Moment bezwładności rozszerzonego obiektu jest zdefiniowany jako:

I = ∫R² DM

Gdzie DM Jest to nieskończenie masy masy i R Jest to odległość między DM i oś obrotu z. Na rycinie 2 oś ta przecina środek masy cm, jednak może to być każdy.

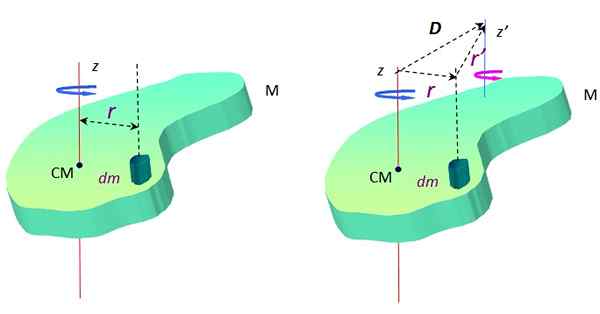Rysunek 2. Obiekt rozszerzony w obrotu wokół dwóch równoległych osi. Źródło: f. Zapata.

Wokół innej osi  z ', Moment bezwładności to:

Siema_z= ∫ (R ')² DM

Teraz, zgodnie z trójkątem utworzonym przez wektory D, R I R ' (Patrz rysunek 2 po prawej), istnieje suma wektorowa:

R + R ' = D   → R ' = D - R

Trzy wektory są w płaszczyźnie obiektu, które mogą być Xy. Pochodzenie układu współrzędnych (0,0) jest wybierane w CM, aby ułatwić następujące obliczenia.

W ten sposób kwadratowy moduł wektora R ' Jest:

Może ci służyć: biofizyka: historia, jakie badania, zastosowania, pojęcia, metody

(R ')² = (D_X- R_X)² +(D_I - R_I)² =

= D_X² + D_I² +R_X² + R_I2 -2d_XR_X - 2 d_IR_I =

= D² + R²  - 2d_XR_X - 2 d_IR_I

Teraz ten rozwój jest zastąpiony w całce momentu bezwładności I_z a także używana jest definicja gęstości DM = ρ.DV:

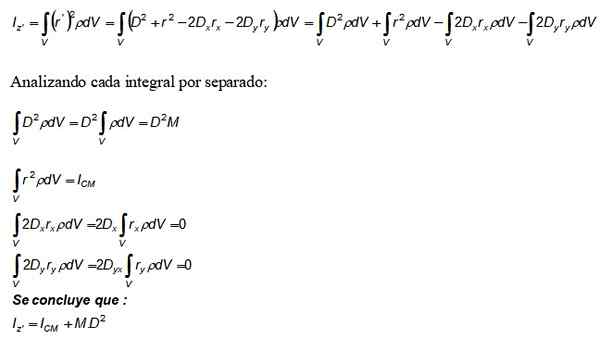
Termin m. D² który pojawia się w twierdzeniu Steinera z pierwszej całki, drugi to moment bezwładności dotyczącej osi, która przechodzi przez CM.

Ze swojej strony trzecie i czwarte całki są warte 0, ponieważ z definicji stanowią one pozycję CM, która została wybrana jako pochodzenie układu współrzędnych (0,0).

Rozwiązane ćwiczenia

-Ćwiczenie rozwiązane 1

Prostokątne drzwi na rycinie 1 mają masę 23 kg, 1,30 szerokości i 2,10 m wysokości. Określ moment bezwładności drzwi dotyczących osi, która przechodzi przez radość, zakładając, że drzwi są cienkie i jednolite.

Rysunek 3. Schemat dla przykładu rozwiązanego 1. Źródło: Zmodyfikowany pixabay.

Rozwiązanie

Z tabeli momentów bezwładności, dla prostokątnej płyty o masie M i wymiarów Do I B, Moment bezwładności w odniesieniu do osi przechodzący przez jej środek masy to: i_Cm = (1/12)M(Do² + B²).

Przyjmowane zostaną jednorodne drzwi (podejście, ponieważ drzwi postaci prawdopodobnie nie są tak bardzo). W tym przypadku środek masy przechodzi przez jego geometryczne centrum. Na rycinie 3 narysowano oś, która przechodzi przez środek masy, a także równolegle do osi, która przechodzi przez radość.

Siema_Cm = (1/12) x 23 kg x (1.30²+2.10²) M² = 11.7 kg.M²

Może ci służyć: co to jest geoid?

Zastosowanie twierdzenia Steinera do osi zielonej obrotu:

I = i_Cm + MD² = 11.7 kg.M² + 23 kg x 0.652 m² = 21.4 kg.

-Ćwiczenie rozwiązane 2

Znajdź moment bezwładności cienkiego jednorodnego pręta, gdy obraca się w odniesieniu do osi, która przechodzi przez jeden z jej końca, patrz rysunek. Czy jest większy czy mniej niż moment bezwładności, gdy obraca się wokół swojego centrum? Ponieważ?

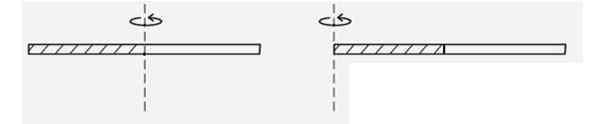Rysunek 4. Schemat dla przykładu rozwiązanego 2. Źródło: f. Zapata.

Rozwiązanie

Według momentów bezwładności moment bezwładności Siema_Cm cienkiego pręta ciasta M i długość L Jest: Siema_Cm = (1/12) ml²

A twierdzenie Steinera stwierdza, że ​​gdy jest obracany wokół osi, która przechodzi przez jeden koniec d = l/2 pozostaje:

I = i_Cm + MD² = (1/12) ml² + M (l/2)² = (1/3) ml²

To jest stare.

Wpływ odległości do osi obrotu nie jest liniowy, ale kwadratowy. Masa, która jest dwukrotnie większa niż inna, będzie miała chwilę bezwładności proporcjonalną do (2d)² = 4d².

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill. 313-340.
2. Georgia State University. Ruch obrotowy. Odzyskane z: Phys.Nthu.Edu.Tw.
3. Twierdzenie o osi równoległej. Odzyskane z: Hiperphysics.Phy-orst.GSU.Edu.
4. Rex, a. 2011. Podstawy fizyki. osoba. 190-200.
5. Wikipedia. Twierdzenie o osi równoległej. Źródło: w:.Wikipedia.org