Twierdzenie Bernoulli

Wyjaśniamy, jakie jest twierdzenie, równania, zastosowania i rozwiązujemy ćwiczenie

Co to jest twierdzenie Bernoulli?

On Twierdzenie Bernoulli Potwierdza, że ​​w idealnym płynie krążącym w przewodzie, energia mechaniczna na jednostkę objętości płynu jest stała we wszystkich odcinkach rurki, niezależnie od tego, że mają one różny poprzeczny odcinek obszaru i wysokości.

Teraz idealny płyn to taki, którego nie można ściskać, więc jego gęstość jest ustalona, ​​niezależnie od wartości ciśnienia.

Ponadto idealny płyn ma zerową lepkość, to znaczy nie ma tarcia między warstwami płynu i ani między płynem a ścianami kanału.

Warunki nieściśliwości i lepkości zerowej są niezbędne do zastosowania twierdzenia Bernoulli. Konieczne jest również, aby przepływ był stacjonarny, to znaczy przepływ nie zmienia się w czasie.

Z drugiej strony przepływ musi być laminarny, więc podczas przejścia kanału nie może być wirowania ani turbulencji.

Równanie Bernoulli

Równanie Bernoulli ma trzy terminy, prace wykonane przez prasę P, energię kinetyczną i energię potencjalną grawitacyjną dla każdej jednostki płynu gęstości objętościowej ρ

Równanie Bernoulliego jest:

Z drugiej strony równanie ciągłości ustala, że ​​w idealnym płynie przepływ jest stały we wszystkich odcinkach rurki przepływowej. To znaczy objętość płynu w tej samej jednostce czasu jest taka sama we wszystkich odcinkach rurki.

Jeśli przepływ jest q, to:

Q = stała

Z:

Q = a · v

Gdzie A jest obszarem przekroju rurki, a V jest prędkością płynu.

Może ci służyć: sztuczne satelity

Należy zauważyć, że w najwęższych odcinkach rurki płyn musi krążyć szybciej, ponieważ pozostaje stały, chociaż się zmienia. Dlatego energia kinetyczna na jednostkę jest większa.

Ponieważ twierdzenie Bernoulliego określa, że ​​energia mechaniczna jest stała we wszystkich sekcjach, w węższych odcinkach większej energii kinetycznej energia potencjalna maleje. 

Energia potencjalna składa się z energii grawitacyjnej na jednostkę objętości plus prace wykonane przez ciśnienie w objętości jednostkowej, zatem przez zmniejszenie energii potencjalnej również zmniejsza ciśnienie.

Podsumowując, połączony efekt zasady ciągłości i twierdzenia Bernoulli powoduje wąskie odcinki rurki przepływowej, gdzie prędkość płynu jest większa, ciśnienie spada w odniesieniu do szerszych sekcji.

Warunki w równaniu Bernoulli

1) Prace wykonane przez ciśnienie na jednostkę objętości 

W odcinku przekroju obszaru do, Płyn porusza ilość S, Z powodu ciśnienia P, które wytwarza siłę f = pienta.

Praca wykonana przez siłę to:

F⋅ s = p⋅ a⋅ s

Ponieważ produkt A⋅S reprezentuje przesuniętą objętość, następnie praca wykonana na jednostkę objętości pasuje numerycznie z wartością P w rozważanym rozdziale.

2) Energia kinetyczna jednostkowej objętości płynu

Ponieważ płyn jest nieściśliwy, jego gęstość ma stałą wartość wywoływaną ρ.

Gdy płyn krąży przez odcinek przekroju A, poruszając ilość s w czasie t, natężenie przepływu wynosi:

Może ci służyć: drugie prawo termodynamiki: wzory, równania, przykłady

v = s/t

A energia kinetyczna wspomnianej części płynu jest obliczana przez:

K = ½ ρ (a⋅s) v²

Ale jeśli przemieszczona objętość (A⋅S) jest jednostką, termin energii kinetycznej zostanie podany przez ½ ρ v².

3) grawitacyjna energia potencjalna jednostkowej objętości płynu na wysokości h 

Dla porcji płynu ciasta M i wysokość H Jeśli chodzi o pewien poziom odniesienia, energię grawitacyjną jest podana przez:

U = m⋅ g⋅ h

Jeśli ciasto M Odpowiada jednolitej części płynu, a następnie masa części odpowiada gęstości ρ, Tak więc potencjalna energia będzie ρ⋅ g⋅ h.

Zastosowania twierdzenia Bernoulli

Wsparcie aerodynamiczne

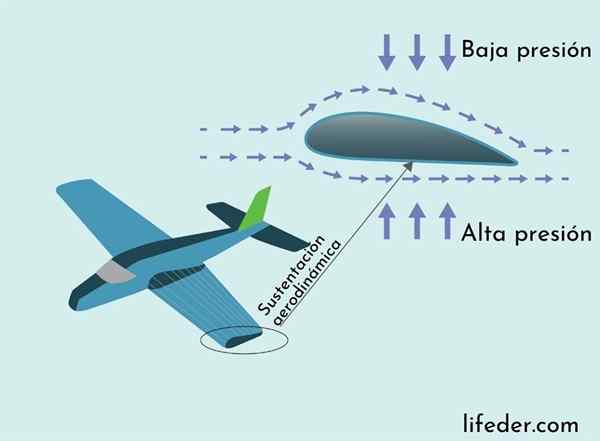Wsparcie aerodynamiczne wyjaśniono twierdzeniem Bernoulli

Siła, która uniemożliwia lot samolotu do zawalenia się, to aerodynamiczna siła wspornika. Siła wsparcia netto jest ukierunkowana pionowo i działa wzdłuż skrzydła płaskiego. Jego pochodzenie jest wyjaśnione przez twierdzenie Bernoulli.

Skrzydło płaszczyzny ma przekrój z dłuższą krzywą u góry i krótszy na dole. To sprawia, że ​​trasa powietrza w pobliżu powierzchni skrzydła u góry, więc powietrze płynie szybciej nad skrzydłem. 

W wyniku twierdzenia Bernoulliego ciśnienie powietrza w górnej części krążącego skrzydła jest mniejsze niż na dole, co powoduje, że siła wywierana przez różnicę ciśnienia jest skierowana w górę, wspierając ciężar płaszczyzny, według niego może być widoczne na poniższym obrazku.

Może ci służyć: fizyka podczas Greków (Antyge Grecja)

Premiera piłek i piłek z efektem krzywej

W niektórych sportach, takich jak piłka nożna, baseball i cricke, doświadczeni gracze wiedzą, jak. Jest to, co się nazywa Uruchomienie efektu.

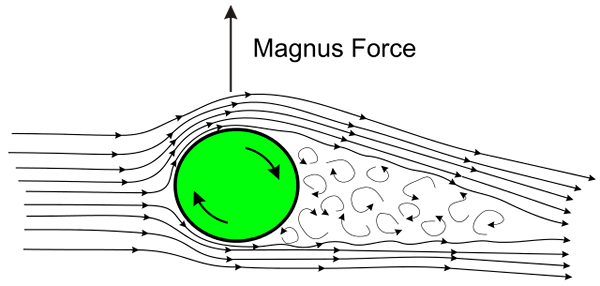Ilustracja efektu Magnusa. Źródło: Wikimedia Commons

Efekt występuje, gdy piłka lub piłka szybko się zmieniają podczas poruszania się w powietrzu. Obrót powoduje, że powietrze do powierzchni piłki jest ciągnięte w dwóch przeciwnych kierunkach, jeden na korzyść kierunku tłumaczenia, a po drugiej stronie, w kierunku przemieszczenia.

W wyniku oporu powietrza wytwarzana jest powierzchnia niskiego ciśnienia na powierzchni piłki i na przeciwległym twarz wysokim ciśnieniem, wytwarzając siłę netto, która kieruje naturalną trajektorię piłki.

Wyjaśnienie tego zjawiska znanego jako Efekt Magnusa Znajduje się dokładnie w twierdzeniu Bernoulliego: gdzie płyn krąży szybkie ciśnienie jest niskie, a z boku, gdzie ciśnienie krąży powoli.

Ćwiczenie rozwiązane

Rurka pozioma ma sekcję A obszar A₁ = 40 centymetrów kwadratowych i kolejny odcinek obszaru A Sekcja A₂ czterokrotnie niższe. Jeśli przepływ wody wynosi 6 l/s, określ różnicę ciśnienia i różnica wysokości w pionowych rurach.

Rozwiązanie 

Zaczynając od równania przepływu, którego wartość wynosi q = 6 l/s:

Q = a · v

Musisz wtedy prędkość w szerokim odcinku wynosi 1,5 m/s, a w wąskim rozciąganiu 6 m/s.

Następnie, stosując i dopasowanie równania Bernoulli na szerokim i wąskim odcinku, uzyskana jest różnica ciśnienia 1700 PA, która odpowiada różnicy wysokości w pionowych rurach 1,72 metra.