Półkole, jak obliczyć obwód, obszar, centroid, ćwiczenia

On półkole Jest to płaska figura wyznaczona średnicą obwodu i jeden z dwóch płaskich kołowych łuków określonych przez wspomnianą średnicę.

W ten sposób półkola graniczy z półkoltowanie, który składa się z płaskiego okrągłego łuku i prostego segmentu, który łączy końce płaskiego okrągłego łuku. Półkola obejmuje półkole i wszystkie punkty wnętrza tego samego.

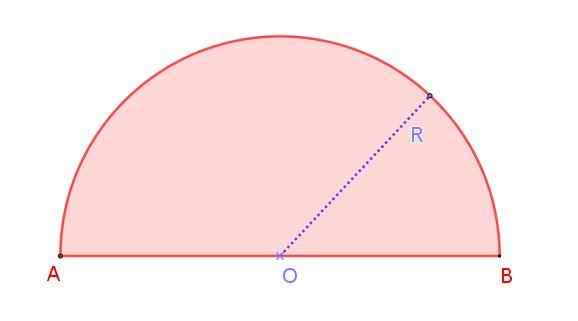Rysunek 1. Radio R Radio Semicricle. Źródło: f. Zapata.

Widzimy to na rycinie 1, które pokazuje radio r rión r, którego miara to połowa średnicy AB. Zauważ, że w przeciwieństwie do okręgu, w którym istnieją nieskończone średnice, w półkolu jest tylko jedna średnica.

Półkuli to postacie geometryczne z wieloma zastosowaniami w architekturze i designie, jak widzimy na następującym obrazie:

Rysunek 2. Seminicírculo jako element dekoracyjny w architekturze. Źródło: Pikist.

[TOC]

Elementy i miary półkola

Elementy półkola to:

1.- Płaski okrągły łuk a⌒b

2.- Segment [ab] 

3.- Wewnętrzne wskazuje półkola złożone z łuku i segmentu A⌒B [AB].

Obwód półkola

Obwód jest sumą konturu łuku plus jest zatem prostego segmentu:

Obwód = długość łuku a⌒b + długość segmentu [AB]

W przypadku radia półkola jego obwód p będzie podany przez formułę:

P = π⋅r + 2⋅r = (π + 2) ⋅r

Pierwszy termin to połowa obwodu obwodu promienia r, a druga to długość średnicy, która jest dwa razy większa niż promień.

Może ci służyć: skale termometryczne

Obszar półkola

Jako półkole jest jednym z płaskich sektorów kątowych, które pozostają przez rysowanie średnicy przez obwód, jego powierzchnia A będzie połową obszaru koła zawierającego radio półkule R:

A = (π⋅r²) / 2 = ½ π⋅r²

Centroid półkola

Centroid półkola znajduje się na osi symetrii do wysokości mierzonej od jej średnicy 4/(3π) razy promień r.

Odpowiada to około 0,424lęrowi, mierzone od środka półkola i na jego osi symetrii, jak pokazano na rycinie 3.

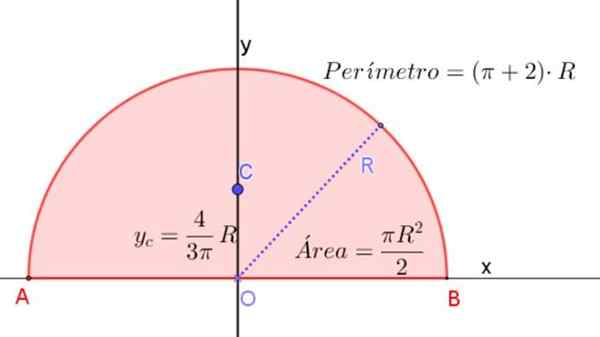Rysunek 3. Półkole radiowe R, wskazujące wzory w celu określenia obszaru, obwodu i lokalizacji jego środka ciężkości. Źródło: f. Zapata.

Moment bezwładności półkola

Moment bezwładności płaskiej figury jest zdefiniowany w odniesieniu do osi, na przykład osi X, na przykład:

Całka kwadratu odległości punktów należących do figury do osi, zróżnicowanie integracji jest nieskończenie małym obszarem, pobranym w pozycji każdego punktu. 

Rycina 4 pokazuje definicję momentu bezwładności i_X półkola radia R, w odniesieniu do osi x, która przechodzi przez jego przekątną:

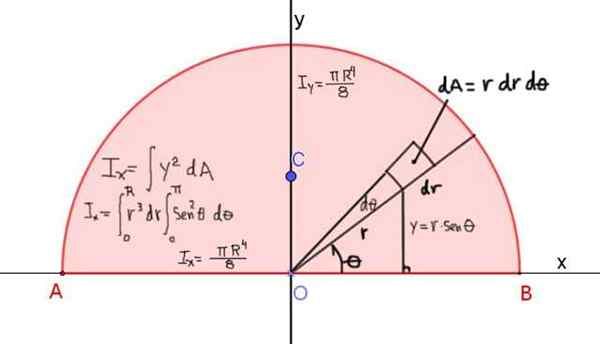Rysunek 4. Definicja momentu bezwładności półkola w odniesieniu do osi x, która przechodzi przez jej przekątną. Wynik pokazano dla momentów bezwładności w odniesieniu do osi x i y. Źródło: f. Zapata.

Moment bezwładności w odniesieniu do osi x jest podany przez:

Siema_X = (π⋅R⁴) / 8

A moment bezwładności w odniesieniu do osi symetrii i jest:

Może ci służyć: pofalowana optyka

IY = (π⋅r⁴) / 8

Pokazuje, że obie momenty bezwładności pokrywają się w ich formule, ale ważne jest, aby podkreślić, że są one skierowane do różnych osi.

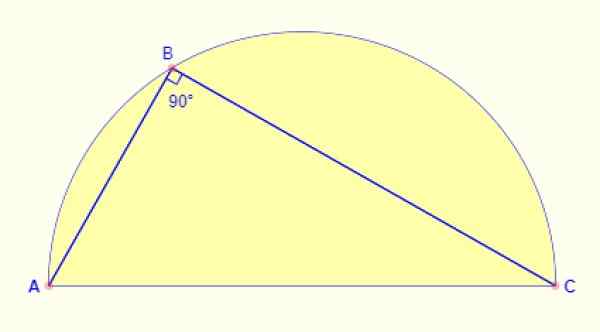
Zarejestrowany kąt

Kąt zarejestrowany w półkolu wynosi zawsze 90º. Niezależnie od tego, która część łuku jest przeniesiona do punktu, kąt utworzony między stronami AB i BC figury jest zawsze prosty.

Rysunek 5. Kąt zarejestrowany w półkolu. Źródło: Math Open Reference.

Rozwiązane ćwiczenia

Ćwiczenie 1 

Określ obwód półkola o promieniu 10 cm.

Rozwiązanie

Przypomnij sobie, że obwód w zależności od promienia jest podawany przez formułę, którą widzieliśmy wcześniej:

P = (2 + π) ⋅r

P = (2 + 3,14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.

Ćwiczenie 2

Znajdź obszar 10 -cm radia półkola.

Rozwiązanie

Formuła obszaru półkola to:

A = ½ π⋅r² = ½ π⋅ (10 cm)² = 50π cm² = 50 x 3,14 cm² = 157 cm².

Ćwiczenie 3

Określ wysokość H środka ciężaru półkurku R = 10 cm mierzonego z jego podstawy, a tym samym jest średnica półkola. 

Rozwiązanie

Centroid jest punktem równowagi półkola, a jego pozycja znajduje się na osi symetrii na wysokości H (średnica półkola):

H = (4⋅r) / (3π) = (4⋅10 cm) / (3 x 3,14) = 4 246 cm

Ćwiczenie 4

Znajdź moment bezwładności półkola w odniesieniu do osi, która pokrywa się z jej średnicą, wiedząc, że półkola jest wykonana z cienkiego arkusza. Jego promień wynosi 10 cm, a jego masa wynosi 100 gramów.

Rozwiązanie

Formuła, która daje moment bezwładności półkola, to:

Może ci służyć: Fizyka stanu solidnego: właściwości, struktura, przykłady

Siema_X = (π⋅R⁴) / 8

Ale jak mówi nam problem, że jest to materialny półkola, wówczas poprzednia relacja musi zostać pomnożona przez gęstość powierzchniową masy półkola, która zostanie oznaczona przez σ.

Siema_X = σ (π⋅r⁴) / 8

Następnie określamy σ, która jest niczym innym jak masą półkola podzielonego między obszar tego samego.

Obszar został określony w ćwiczeniu 2, a wynik wynosił 157 cm². Wtedy powierzchowna gęstość tego półkola będzie:

σ = 100 gramów / 157 cm² = 0,637 g/cm²

Wtedy moment bezwładności w odniesieniu do średnicy zostanie obliczony w następujący sposób:

Siema_X = (0,637 g/cm²) [31416 ⋅ (10 cm)⁴]/ 8

Wynikły:

Siema_X = 2502 G⋅CM²

Ćwiczenie 5

Określić moment bezwładności półkola o promieniu 10 cm zbudowany z arkusza materiału o gęstości powierzchniowej 0,637 g/cm² przez oś, która przechodzi przez jego centroid i jest równoległa do jego średnicy.

Rozwiązanie

Aby rozwiązać to ćwiczenie, należy zapamiętać twierdzenie Steinera o momentach bezwładności równoległych osi, co mówi:

Moment bezwładności I w odniesieniu do osi, która znajduje się w odległości H Centroid jest równa suma momentu bezwładności I_C Jeśli chodzi o oś, która przechodzi przez centroid i jest równoległa do pierwszego i iloczyn ciasta przez kwadrat oddzielenia dwóch osi.

I = i_C + M h²

W naszym przypadku wiadomo, że jest to moment bezwładności w odniesieniu do średnicy, która została już obliczona w ćwiczeniu 4. H zna także między średnicą a środkiem ciężkim, który został obliczony w ćwiczeniu 3.

Musimy tylko wyczyścić IC:

Siema_C = I - m h²

Siema_C = 2502 G⋅CM² - 100G ⋅ (4246 cm)² powodując moment bezwładności osi równolegle do średnicy, która przechodzi przez centroid, wynosi: 

Siema_C = 699,15 G⋅CM²

Bibliografia

1. Alexander, zm. 2013. Geometria. 5. Wydanie. Cengage Learning.
2. Odniesienie do otwartego matematyki. Półkole. Odzyskane z: Mathpenref.com.
3. Formuły wszechświata.Półkole. Odzyskane z: Universoformulas.com.
4. Formuły wszechświata. Obszar półkola. Odzyskane z: Universoformulas.com.
5. Wikipedia. Półkole. Źródło: w:.Wikipedia.com.