Zmniejszenie podobnych terminów

Jaka jest redukcja podobnych terminów?

Zmniejszenie podobnych terminów Jest to metoda stosowana do uproszczenia wyrażeń algebraicznych. W wyrażeniu algebraicznym podobne terminy to te, które mają tę samą zmienną; to znaczy, mają te same niewiadomy reprezentowane przez list i mają te same wykładniki.

W niektórych przypadkach wielomiany są obszerne i aby osiągnąć rozwiązanie, musisz spróbować zmniejszyć ekspresję; Jest to możliwe, gdy są podobne terminy, które można połączyć, stosując operacje algebraiczne i właściwości, takie jak suma, odejmowanie, mnożenie i podział.

Wyjaśnienie

Podobne terminy są tworzone przez te same zmienne o tych samych wykładnikach, aw niektórych przypadkach różnią się one jedynie ich współczynniki numeryczne.

Ci, którzy nie mają zmiennych, są również uważane za podobne warunki; to znaczy te terminy, które mają tylko stałe. Zatem na przykład następujące są podobne warunki:

• 6x² - 3x². Oba terminy mają tę samą zmienną x².
• 4²B³ + 2²B³. Oba terminy mają te same zmienne²B³.
• 7 - 6. Warunki są stałe.

Te terminy, które mają te same zmienne, ale z różnymi wykładnikami nazywane są terminami niezimarowymi, takimi jak:

• 9²B + 5AB. Zmienne mają różne wykładniki.
• 5x + i. Zmienne są różne.
• B - 8. Jeden termin ma zmienną, drugi jest stały.

Identyfikując podobne terminy, które tworzą wielomian, można je sprowadzić do jednego, łącząc wszystkie osoby, które mają te same zmienne z równymi wykładnikami. W ten sposób wyrażenie jest uproszczone poprzez zmniejszenie liczby terminów, które go komponują, a obliczenie jego rozwiązania jest ułatwione.

Jak dokonać redukcji podobnych terminów?

Zmniejszenie podobnych warunków odbywa się poprzez zastosowanie własności asocjacyjnej wartości dodawania i dystrybucji produktu. Korzystając z następującej procedury, można dokonać zmniejszenia warunków:

• Po pierwsze, podobne warunki są zgrupowane razem.
• Współczynniki (liczby towarzyszące zmiennym) podobnych terminów są dodawane lub odejmowane, a właściwości asocjacyjne, przemienne lub dystrybucyjne są stosowane, jak może być sprawa.
• Następnie uzyskane nowe warunki są pisane, umieszczając przed nimi znak wynikający z operacji.

Może ci służyć: dyskretna matematyka

Przykład

Zmniejsz warunki następującego wyrażenia: 10x + 3y + 4x + 5y.

Rozwiązanie

Najpierw warunki są nakazane do grupowania tych, które są podobne, stosując własność przemienną:

10x + 3y + 4x + 5y = 10x + 4x + 3y + 5y.

Następnie stosuje się właściwość dystrybucyjną, a współczynniki towarzyszące zmiennym są dodawane w celu uzyskania zmniejszenia terminów:

10x + 4x + 3y + 5y

= (10 + 4) x + (3 + 5) i

= 14x + 8y.

Aby zmniejszyć podobne warunki, ważne jest, aby wziąć pod uwagę znaki, które mają współczynniki towarzyszące zmiennej. Istnieją trzy możliwe przypadki:

Redukcja podobnych terminów z równymi znakami

W takim przypadku współczynniki są dodawane, a przed wynikiem umieszczono znak warunków. Dlatego jeśli są pozytywne, powstałe terminy będą pozytywne; W przypadku, gdy terminy są ujemne, wynik będzie miał znak (-) w towarzystwie zmiennej. Na przykład:

a) 22ab² + 12ab² = 34 AB².

b) -18x³ - 9x³ - 6 = -27x³ - 6.

Zmniejszenie podobnych terminów CNa różnych znakach

W takim przypadku współczynniki odejmuje się, a przed wynikiem umieszczono znak głównego współczynnika. Na przykład:

a) 15x²i - 4x²i + 6x²i - 11x²I

= (15x²i + 6x²Y) + ( - 4x²i - 11x²I)

= 21x²Y + (-15x²I)

= 21x²i - 15x²I

= 6x²I.

b) -5a³B + 3 a³B - 4a³B + a³B

= (3 A³B + a³b) + (-5a³B - 4a³B)

= 4a³B - 9a³B

= -5 a³B.

W ten sposób, aby zmniejszyć podobne terminy, które mają różne znaki, utworzony jest pojedynczy termin addytywny w stosunku do wszystkich tych, które mają znak dodatni (+), dodaje się współczynniki, a wynikowi towarzyszą zmienne.

Może ci służyć: jednolite okrąg: funkcje trygonometryczne i aplikacje

W ten sam sposób powstaje termin odejmujący, z wszystkimi tymi terminami, które mają znak ujemny (-), dodaje się współczynniki, a wynikowi towarzyszą zmienne.

Wreszcie suma dwóch utworzonych terminów są odjęte, a znak największego jest umieszczony w wyniku.

Redukcja podobnych terminów w operacjach

Zmniejszenie podobnych terminów jest operacją algebry, którą można zastosować w sumie, odejmowaniu, mnożaniu i podziału algebraicznym.

W sumach

Gdy masz kilka wielomianów o podobnych warunkach, aby je zmniejszyć, warunki każdego wielomianu są uporządkowane zachowanie ich znaków, są one pisane po innych, a podobne warunki są zmniejszone. Na przykład masz następujące wielomiany:

3x - 4xy + 7x²i + 5xy².

- 6x²i - 2xy + 9 xy² - 8x.

W odejściach

Aby odejmować wielomian od innego, minuend jest pisany, a następnie odejmowanie go za pomocą zmienionych znaków, a następnie dokonuje się zmniejszenia podobnych terminów. Na przykład:

5³ - 3AB² + 3b²C

6ab² + 2³ - 8b²C

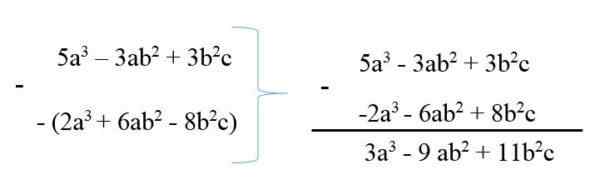
Zatem wielomiany podsumowano w 3a³ - 9ab² + 11b²C.

W mnożkach

W produkcie wielomianowym terminy, które składają się na mnożenie dla każdego terminu, który tworzy mnożnik, biorąc pod uwagę, że znaki mnożenia pozostają takie same, jeśli są one dodatnie, jeśli są dodatnie.

Zmieni się one tylko podczas mnożenia przez negatywny termin; To znaczy, gdy dwa warunki tego samego znaku pomnożą wynik, wynik będą dodatnie (+), a gdy będą miały różne znaki, wynik będzie ujemny (-).

Na przykład:

a) (a + b) _* (A + B)

= a² + AB + AB + B²

= a² + 2AB+ b².

b) (A + B) _* (A - B)

= a² - AB + AB - B²

= a² - B².

taksówka) _* (A - B)

= a² - AB - AB + B²

= a² - 2AB+ b².

W podziałach

Kiedy chcesz zmniejszyć dwa wielomiany poprzez podział, trzeci wielomian musi.

Może ci służyć: Turs Tukey: Co to jest w przypadku przykładu rozwiązanego ćwiczenia

W tym celu warunki dywidendy i dzielnika muszą być uporządkowane, od lewej do prawej, aby zmienne w obu były w tej samej kolejności.

Działa jest następnie wykonywana, zaczynając od pierwszego okresu lewej strony dywidendy między pierwszą po lewej stronie dzielnicy, zawsze biorąc pod uwagę znaki każdego terminu.

Na przykład zmniejsz wielomian: 10x⁴ - 48x³i + 51x²I² + 4xy³ - 15Y⁴ Dzielenie go między wielomianem: -5x² + 4xy + 3y².

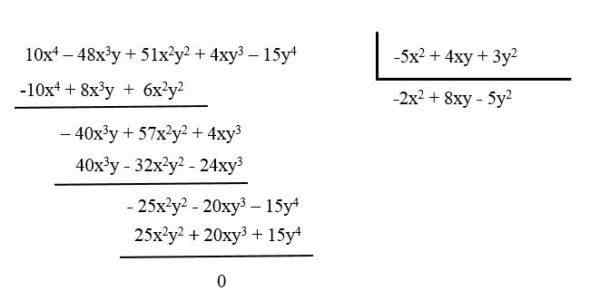
Powstały wielomian wynosi -2x² + 8xy - 5y².

Rozwiązane ćwiczenia

Pierwsze ćwiczenie

Zmniejsz warunki wyrażenia algebraicznego:

15a² - 8ab + 6a² - 6ab - 9 +4a² - 13 ab.

Rozwiązanie

Zastosowana jest właściwość przemienna sumy, grupując warunki, które mają te same zmienne:

15a² - 8ab + 6a² - 6ab + 9 + 4a² - 13

= (15a² + 6th² + 4²) + ( - 8AB - 6AB) + (9 - 13).

Następnie stosuje się właściwość dystrybucyjną mnożenia:

15a² - 8ab + 6a² - 6ab + 9 + 4a² - 13

= (15 + 6 + 4) a² + ( - 8 - 6) AB + (9 - 13).

Wreszcie są one uproszczone poprzez dodanie i odejmowanie współczynników każdego terminu:

15a² - 8ab + 6a² - 6ab + 9 + 4a² - 13

= 25a² - 14AB - 4.

Drugie ćwiczenie

Uprości iloczyn następujących wielomianów:

(8x³ + 7xy²)_*(8x³ - 7 xy²).

Rozwiązanie

Każdy termin pierwszego wielomianu jest mnożony przez drugi, biorąc pod uwagę, że znaki terminów są różne; Dlatego wynik jego mnożenia będzie ujemny, a także należy zastosować prawa wykładników.

(8x³ + 7xy²) _* (8x³ - 7xy²)

= 64 x⁶ - 56 x³_* Xy² + 56 x³_* Xy² - 49 x²I⁴

= 64 x⁶ - 49 x²I⁴.