Drugie linie

Drewno drzwi tego ogrodu są chętne w taki sposób, że określają suche linie. Źródło: f. Zapata. Pxhere.com

Jakie są suche linie?

W samolocie Drugie linie To te, które przecinają inne linie i krzywe. W przypadku dwóch linii jego skrzyżowanie jest punktem, podczas gdy linia sekundowa na krzywej, przecina ją w dwóch lub więcej punktach.

Uważnie obserwuj ogrodzenie górnej postaci. Na nim narysowano kilka prostych kolorów, oznaczonych jako L₁, L₂ i ja₃. Strzałki po obu stronach oznaczają, że linie są przedłużane w nieskończoność.

Cóż, linie l₁, L₂ i ja₃ Suszą się nawzajem, ponieważ każda z nich jest wycięta w fioletowych punktach.

Ponadto linie l₁ i ja₂, Jak l₁ i ja₃, Określą 4 kąty ze sobą, dwa ostre, a drugie tępe, podczas gdy linie l₂ i ja₃ Są prostopadłe, co oznacza, że ​​4 kąt określone przez nich są proste.

Dwie równoległe linie nigdy nie mogą być suche, ponieważ ze względu na ich stan nie mają punktów okoliczności. Z kolei linie przypadkowe nie są suche, ponieważ mają więcej niż jeden punkt wspólnego.

Charakterystyka linii suszenia

• Dwie sekundy mają unikalny punkt jako skrzyżowanie.
• Stoki dwóch linii suszenia muszą być inne. tak m₁ Jest to nachylenie linii l₁, oraz m₂ Jest to nachylenie linii l₂, wtedy spełnia się, że m₁ ≠ m₂.
• Zbocza dwóch linii suszenia prostopadłych do siebie, których odpowiednią stoki to m₁ oraz m₂, Spełniają związek m₁ = -1/ m₂. Ponadto produkt skalarny między dwoma wektorami v I Lub zawarty w tych wierszach jest zerowy, ponieważ definicja produktu skalarnego jest v Lub = v ∙ u ∙ cos θ, będąc θ kąt między wektorami.
• Linia może być segntem do krzywej lub innej liczby geometrycznej.
• Podczas przecinania dwie linie suszenia generują 4 kąty, identyczne dwa do dwóch lub identyczne z sobą.

Może ci służyć: równania ułamkowe

Jak wiedzieć, czy dwie linie są suche

Z charakterystyk opisanych powyżej linii suszenia możliwe jest ustalenie trzech kryteriów, aby dowiedzieć się, czy dwie linie są suche:

-Porównanie stoków. Jeśli są różne, linie są suche.

-Przeprowadzanie produktu skalarnego między dwoma wektorami zawartymi w tych liniach, zwanych Dyrektorzy. Jeśli produkt skalarny jest nieważny, linie są suche i prostopadłe, a jeśli nie jest zero, można poznać minimalny kąt między nimi, który jest ostrym kątem istniejącym między liniami.

Pod warunkiem, że kąt ten różni się od 0º, linie są suche, a jeśli jest równe 0º, to jest to równoległe linie.

-Bezpośrednio obliczanie ostrego kąta, który istnieje wśród linii, znany ich zbocze. Można to zrobić poprzez wzór, który odnosi styczną wspomnianego kąta ze zboczami.

Niech m₁ oraz m₂ zbocza i θ ostry kąt między nimi. Styczna θ jest podana przez:

Rodzaje linii suszenia

Kiedy dwie linie suszą się nawzajem, mogą być następującymi typami:

• Skośny, Jeśli po cięcie tworzą dwa ostre kąty i dwa tępe kąty. Kąty te są uzupełniające, to znaczy suma miary kąta plus jeden z kątu rozwatanego jest równy 180º. W sumie suma 4 kątów wynosi 360º.
• Prostopadły, Te, które przecinają 4 kąty równe 90º.

Jak znaleźć skrzyżowanie między dwiema liniami

Jeśli suszą dwie linie, mają tylko jeden punkt cięcia, który rozwiązuje układ dwóch równań liniowych z dwoma niewiadomymi. Jeśli linie są podane w ogóle: ax + przez = c, wspomniany system równań wynosi:

Może ci służyć: nieskończony zestaw: właściwości, przykłady

Do₁x + b₁ y = c₁

Do₂x + b₂ y = c₂

Jak znaleźć skrzyżowanie między linią a krzywą

Znając równania zarówno linii, jak i krzywej, proponowany jest układ równań i, którego rozwiązania odpowiadają punktom przecięcia. Jeśli w systemie brakuje rozwiązania, linia nie jest segntem do krzywej, ani też nie istnieje pojedynczy punkt cięcia, ponieważ w takim przypadku linia jest styczna do krzywej.

Aby linia do wyschnięcia, jak stwierdzono na początku, układ równań musi mieć dwa lub więcej rozwiązań.

Przykłady linii suszenia

Samolot kartezjański

Płaszczyzna kartezjański jest określany przez dwie linie, zwane Oś x I Oś y, odpowiednio poziome i pionowe. Te linie są prostopadłe, a ich punkt przecięcia jest nazywany Pochodzenie układu współrzędnych, lub po prostu pochodzenie.

Przekątna wielokąta

Polygon to płaska liczba trzech lub więcej stron, które łączą się w punktach zwanych wierzchołkami. Segment, który dołącza do dwóch nieobserwowych wierzchołków, jest przekątną wielokąta, a linia zawierająca wspomniany segment jest segntem do danego wielokąta.

Lina o obwodzie

Lina obwodu jest segmentem, który łączy dwa punkty. Główna lina to średnica, która koniecznie przechodzi przez środek obwodu. Cóż, linia zawierająca dowolną linę, w tym średnica, jest linią suszenia do obwodu.

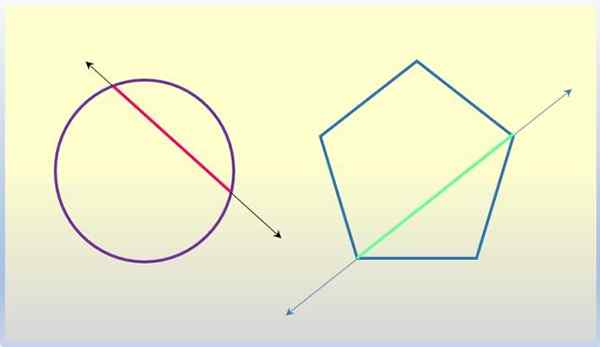Drugie linie do liczb geometrycznych. Źródło: f. Zapata.

Klucz krzyżowy

Z tym narzędziem rozluźnia się nakrętki, które trzymają opony przy kółkach. Ramiona tworzą linie suche i jednocześnie prostopadłe.

Może ci służyć: proporcjonalna różnica

Teksty alfabetu

Niektóre litery alfabetu składają się z prostych udarów, które determinują siekantę. Na przykład litera X składa się z dwóch uderzeń, które są wycięte razem w jednym punkcie, a litera T składa się z dwóch prostopadłych linii.

Rozwiązane ćwiczenia

Ćwiczenie 1

Określ, czy linie podane przez:

L₁ : y = 5x - 3

L₂ : y = -2x+1

Rozwiązanie

Nachylenie linii podanej w postaci y = mx + b jest wartością m, to znaczy współczynnika towarzyszącego x. Od m₁ = 5 i M₂ = -2, które są różne, stwierdza się, że linie są suche.

Ćwiczenie 2

Jaki jest ostry kąt między liniami ćwiczenia 1?

Rozwiązanie

Wartości M są bezpośrednio zastępowane₁ = 5 i M₂ = -2 w wzorze podanym w poprzednich sekcjach:

Dlatego kąt między liniami wynosi θ = arctg 0.777… = 37.9º.

Ćwiczenie 3

Jakie jest przecięcie linii poprzednich ćwiczeń?

Rozwiązanie

Układ równań jest proponowany w następujący sposób:

Którego rozwiązanie to: x = 4/7; y = -1/7 (można je rozwiązać dowolną z metod rozdzielczości dla systemów równań lub z kalkulatorem).

Dlatego punkt przecięcia linii jest: P (4/7; -1/7).

Bibliografia

1. Geometria analityczna.Informacje. Drugie linie. Odzyskane z: Geometrianalitycs.Informacje.
2. Larson, r. 2006. Obliczanie za pomocą geometrii analitycznej. 8. Wydanie. McGraw Hill.
3. Linie, które krzyżują. Odzyskane z: Teacheraltuna.com.
4. Requena, ur. Drugie linie. Odzyskane z: Universoformulas.com.
5. Villena, m. Geometria analityczna w R3. Źródło: DSPACE.Espol.Edu.Ec.