Charakterystyka, równania i przykłady praw obok

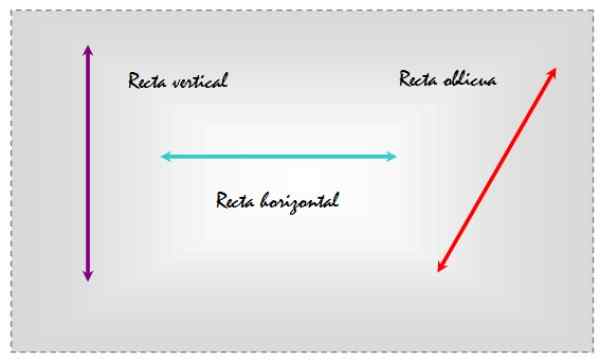
skośne linie Są tymi, które są pochylone, albo w odniesieniu do płaskiej powierzchni lub innej linii, która wskazuje na konkretny adres. Jako przykład, rozważ trzy linie narysowane w płaszczyźnie, które pojawiają się na poniższym rysunku.

Znamy ich odpowiednie pozycje względne, ponieważ porównujemy je z linią odniesienia, która zwykle jest Oś x To oznacza poziome.

Rysunek 1. Pionowe, poziome i ukośne linie w tej samej płaszczyźnie. Źródło: f. Zapata.

W ten sposób, wybierając poziome odniesienie, lewa linia jest pionowa, środek jest pozioma, a ta po prawej jest ukośna, ponieważ jest pochylona w odniesieniu do codziennych linii odniesienia.

Teraz linie na tej samej płaszczyźnie, takie jak powierzchnia papieru lub na ekranie, zajmują różne pozycje względne siebie, w zależności od tego, czy przecinają się, czy nie. W pierwszym przypadku są one proste, podczas gdy w drugim są równoległe.

Z drugiej strony linie suszenia mogą być również skośne lub prostopadłe proste linie. W obu przypadkach zbocza linii są różne, ale linie ukośne powstają między sobą α i β, inne niż 90º, podczas gdy kąty określone przez linie prostopadłe wynoszą zawsze 90º.

Na poniższym rysunku definicje te zostały podsumowane:

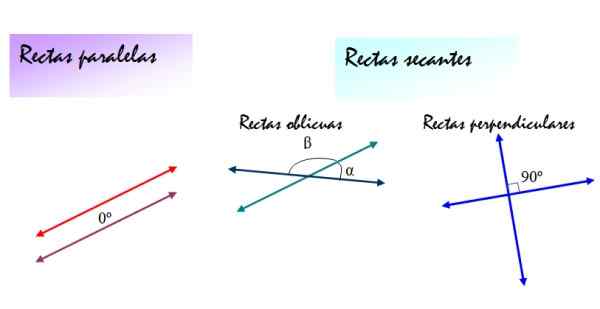Rysunek 2. Względne pozycje między liniami: równoległe, ukośne i prostopadłe różnią się pod kątem, które tworzą się ze sobą. Źródło: f. Zapata.

[TOC]

Równania

Aby poznać względne pozycje linii w płaszczyźnie, należy znać kąt, który tworzą ze sobą. Zauważ, że linie to:

Może ci służyć: obliczanie podejść z wykorzystaniem różnicowych

Równoległy: Jeśli mają to samo zbocze (równy kierunek) i nigdy nie przecinają się, więc ich punkty są równoległe.

Przypadki: Kiedy wszystkie ich punkty pokrywają się i dlatego mają to samo zbocze, ale odległość między ich punktami wynosi zero.

Sekundy: Jeśli twoje kolczyki są różne, odległość między ich punktami jest różna, a przecięcie jest jednym punktem.

Tak więc sposób na poznanie, czy dwie linie w płaszczyźnie są suche lub równoległe, jest przez jego nachylenie. Kryteria równoległości i prostopadłości linii są następujące:

Być dwiema liniami l₁ i ja₂ należący do samolotu, którego oczekują odpowiednio m₁ oraz m₂. Te linie są równoległe, jeśli m₁ = m₂ i są prostopadłe, gdy m₁= -1/m₂

Jeśli znając zbocza dwóch linii w płaszczyźnie, żadne z powyższych kryteriów nie jest spełnione, dochodzimy do wniosku, że linie są ukośne. Znając dwa punkty linii, nachylenie jest natychmiast obliczane, jak zobaczymy w następnym rozdziale.

Możesz dowiedzieć się, czy dwie linie są suche lub równoległe do znalezienia ich skrzyżowania, rozwiązywanie układu równań, które formują: jeśli istnieje rozwiązanie, jeśli nie są równoległe, ale jeśli roztwory są nieskończone, linie są przypadkowe.

Jednak to kryterium nie informuje nas o kącie między tymi liniami, nawet jeśli mają one skrzyżowanie.

Aby poznać kąt między liniami, potrzebne są dwa wektory Lub I v które należą do każdego z nich. W ten sposób można poznać kąt, który tworzą przez produkt skalarny wektorów, zdefiniowany w ten sposób:

Lub• •v =Lub.v.cos α

Równanie linii w płaszczyźnie

Linia w płaszczyźnie kartezjańskiej można reprezentować na kilka sposobów, na przykład:

Może ci służyć: ogólne równanie paraboli (przykłady i ćwiczenia)

-Forma oczekująca: Tak M Jest to nachylenie linii i B Jest to przecięcie linii z osą pionową, równanie linii to y = MX +B.

-Ogólne równanie dla linii prostej: Ax + przez + c = 0, Gdzie M = A/B To jest zbocze.

W płaszczyźnie kartezjańskiej linie pionowe i poziome są szczególnymi przypadkami równania linii.

-Pionowe linie: x = a

-Linie poziome: y = k

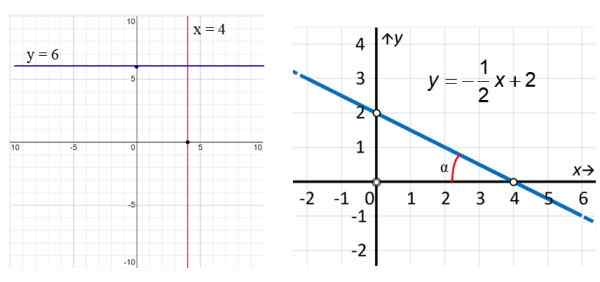Rysunek 3. Po lewej stronie linia pionowa x = 4 i linia pozioma y = 6. Po prawej przykład linii ukośnej. Źródło: f. Zapata.

W przykładach ryc. 3 pionowa czerwona linia ma równanie x = 4, podczas gdy linia równoległa do osi x (niebieska) ma równanie y = 6. Jeśli chodzi o odpowiednią linię, widzimy, że jest ona ukośna i aby znaleźć jego równanie, używamy punktów podkreślonych na rysunku: (0.2) i (4.0) w ten sposób:

M = (i₂ - I₁) / (X₂ - X₁) = (2 - 0) / (0 - 4) = - ½

Cięcie tej linii za pomocą osi pionowej to y = 2, Jak zauważono z grafiki. Z tą informacją:

y = (-½) x+2

Określenie kąta nachylenia w odniesieniu do osi x jest proste. Czuję to:

α = ARCTG (2/4) = 26.6th

Dlatego kąt dodatni od osi x do linii wynosi: 180º - 26.6 = 153.4

Przykłady skośnych linii

Rysunek 4. Przykłady skośnych linii. Źródło: Ian Patterson gniew [cc by (https: // creativeCommons.Org/licencje/według/2.0)]. Pochyczna wieża Pizy. Pixabay.

Skośne linie pojawiają się w wielu miejscach, chodzi o zwrócenie uwagi na znalezienie ich w architekturze, sporcie, okablowaniu dostaw energii elektrycznej, rurach i w wielu innych miejscach. W naturze obecne są również skośne linie, jak zobaczymy poniżej:

Może ci służyć: zasady pochodzenia (z przykładami)

Promienie światła

Światło słoneczne rozprzestrzenia się w linii prostej, ale zaokrąglony kształt ziemi wpływa na sposób, w jaki światło słoneczne wpływa na powierzchnię.

Na poniższym obrazku możemy wyraźnie docenić, że promienie słoneczne wpływają prostopadle w regionach tropikalnych, ale zamiast tego pojawiają się ukośnie na powierzchnię w regionach umiarkowanych i na biegunach.

Dlatego promienie słoneczne przemieszczają się w dłuższej odległości przez atmosferę, a także ciepło rozprzestrzeniają się na większej powierzchni (patrz rysunek). W rezultacie obszary bliskie biegunom są chłodniejsze.

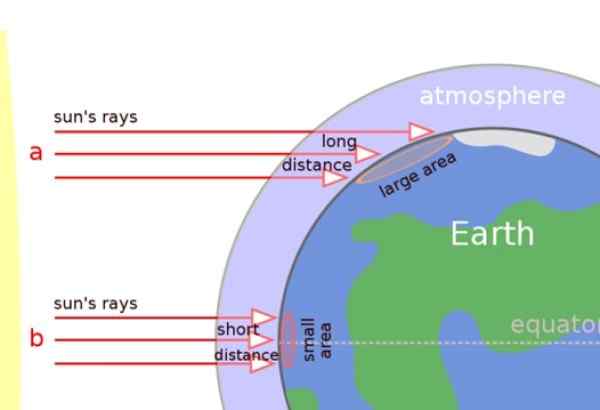Rysunek 5. Promienie słoneczne ukośnie wpływają na strefy umiarkowane i bieguny, jednak są one mniej więcej prostopadłe w tropikach. Źródło: Wikimedia Commons.

Linie, które nie są w tej samej płaszczyźnie

Gdy dwie linie nie znajdują się w tej samej płaszczyźnie, nadal mogą być ukośne lub Pochwalony, Jak są również znane. W tym przypadku jego dyrektorzy nie są równoległe, ale nie należą do tej samej płaszczyzny, linie te nie mają przecięcia.

Na przykład linie na prawej figurze są wyraźnie w różnych samolotach. Jeśli wyglądają z góry, obserwuje się, że skutecznie się przekraczają, ale nie mają wspólnego punktu. Po prawej widzimy koła rowerowe, których promienie wydają się przekraczać, gdy wyglądają prosto przed.

Rysunek 6. Skośne linie należące do różnych samolotów. Źródło: Left F. Zapata, prawy pixabay.

Bibliografia

1. Geometria. Dyrektor wektorowy linii. Odzyskane z: Juanbragado.Jest.
2. Larson, r. 2006. Obliczanie za pomocą geometrii analitycznej. 8. Wydanie. McGraw Hill.
3. Matematyka to gra. Linie i kąty. Odzyskane z: Juntadeandlucia.Jest.
4. Linie, które krzyżują. Odzyskane z: Teacheraltuna.com.
5. Villena, m. Geometria analityczna w R3. Źródło: DSPACE.Espol.Edu.Ec.