Powód do zmiany

Jaki jest powód zmiany?

powód do zmiany Jest to wielkość matematyczna, która określa zmianę zmiennej lub wielkości fizycznej w odniesieniu do innej. Na przykład prędkość jest powodem zmiany pozycji w odniesieniu do czasu.

Zmiana wielkości X, Jest oznaczony greckim tekstem δ (czyta „Delta”) i jest napisany δx. Oblicza to różnica między wartością końcową a początkową: Δx = x_finał- X_wstępny.

Jeśli wielkość X jest związane z inną wielkością I, To również ma zmianę, zwaną Δy = y_finał- I_wstępny, Powód zmiany y w odniesieniu do x jest zdefiniowany jako iloraz:

Który, używając notacji z Delta wcześniej, pozostaje tak:

Ten iloraz jest znany jako Zwiększyć iloraz z I z szacunkiem do X albo średni lub średni współczynnik zmiany.

W ten sposób możesz zdefiniować wielkości, takie jak wskaźnik wzrostu populacji, prędkość, z którą obiekt, szybkość bezrobocia, przepływ wody przez rury i wiele innych. Wszystkie te kwoty są w efekcie zmiany.

Dlaczego ważne jest obliczenie przyczyny zmiany?

Wiele interesujących wielkości nie pozostają niezmienne, ale doświadczają zmian i często te zmiany podążają za sobą w czasie. Stąd znaczenie obliczenia przyczyny zmiany wielkości w czasie.

Na przykład istnieje prosty przypadek obiektu, który porusza się wzdłuż linii prostej, który może być osą poziomą lub osą X. Telefon komórkowy (samochód, rower, osoba, która idzie lub działa ...) ciągle zmienia swoją pozycję, gdy mija czas T.

Następnie powód zmiany pozycji obiektu Δx w przedziale czasowym ΔT jest znany jako średnia prędkość:

Kolejny telefon komórkowy, który podróżuje przez tę samą linię prostą, może to zrobić z inną prędkością, czy to lub mniej, i w ten sposób odróżnia się od pierwszego telefonu komórkowego (ponieważ jest wolniejszy lub szybszy).

Na przykład płaski korytarz 100 -metrowy będzie miał średni kurs wymiany w swojej pozycji znacznie większy niż maraton lub osoba, która cicho idzie po ulicy.

Prędkość jest typowym przykładem współczynnika zmian, ale niektóre interesujące wielkości, które również doświadczają zmian w czasie, to: temperatura, objętość płynu, ładunek elektryczny, populacja bakterii i wiele innych.

Znając swój powód zmiany, możesz wiele wiedzieć o sposobie ewolucji tych wielkości.

Jednostki przyczyny zmiany

Stosunek jest stosunkiem między dwoma wielkościami, powstałe jednostki będą również ilorazem jednostek użytych do ich pomiaru. Na przykład prędkość jest długością między czasem, ponieważ jest to powód zmiany pozycji w odniesieniu do czasu.

W ten sposób jednostki prędkości mogą wynosić metry/drugie, kilometry/godzinę, mile/godzinę i wiele innych kombinacji.

Jak obliczono powód zmiany?

Średnie przyczyna lub kurs wymiany między dwoma wielkościami jest łatwo obliczany podczas wykonywania ilorazu między odpowiednimi wariantami każdego z nich, zgodnie z wzorem:

Zmiany wielkości można podać za pomocą tabel standardowych lub być określone przez wykres, z których odpowiednie wartości I I X (Zobacz ćwiczenia rozwiązane na końcu).

Z drugiej strony:

A ekspresja prawej jest dokładnie nachyleniem linii, której stwierdzono, że średnim przyczyną zmiany jest nachyleniem linii sekundowej do wykresu y w zależności od x.

Oznaki powodu zmiany

Zgodnie z daną definicją przyczynę zmian może być pozytywna lub ujemna, w zależności od tego, w jaki sposób związane z nimi wielkości mogą się różnić, ponieważ mogą one rosnąć lub zmniejszać, zgodnie z.

Jeśli przyczyna zmiany jest pozytywna, oznacza to, że się zmienia I i w X Byli tym samym znakiem, to znaczy, I zwiększone i X On też. Lub tyle I Jak X Zmniejszyli się.

Jednak gdy przyczyna zmiany jest ujemna, oznacza to, że jedna z wielkości wzrosła, a druga spadła.

Natychmiastowa zmiana rozum

Często jest to o wiele bardziej interesujące. W takim przypadku konieczne jest, aby zmiana ΔX była wyjątkowo niewielka, dążąc do 0 (ale bez osiągnięcia 0, ponieważ podział między 0 nie jest zdefiniowany).

Nazywa się to „biorącym limit”, aw takim przypadku stosunek natychmiastowej zmiany nazywa się „pochodną” I z szacunkiem do X i jest oznaczony jako Dy/DX; Więc:

Współczynnik lub szybkość zmiany chwilowej równa się również nachyleniu linii, ale w tym przypadku jest to nachylenie linii stycznej do wykresu I przeciw X.

Proste przykłady

Wzrost osoby

Ponieważ się rodzą, dzieci rosną w tempie określonym przez kilka czynników, w tym genetyka i jedzenie. Najwyższe stopy wzrostu występują w pierwszym roku życia; Później, w dzieciństwie, a potem w okresie dojrzewania, dzieci zwykle doświadczają „rozciągania”, to znaczy przyczyny zmiany wysokości w odniesieniu do czasu, a następnie zmniejszają.

Po okresie dojrzewania chłopcy nadal rosną, ale tempo zmniejsza.

Kawa fajna

Wiadomo fakt, że kawa lub gorąca zupa są stopniowo chłodzone, gdy pozostawia się w temperaturze pokojowej. Jednak szybkość chłodzenia zwalnia bliżej temperatury kawy lub zupę w temperaturze pokojowej.

Jednym ze sposobów modelowania tego zjawiska jest Newton Cooling Law, Zgodnie z tym, szybkość przenoszenia ciepła jest proporcjonalna do różnicy między temperaturą substancji a temperaturą otoczenia. Stała proporcjonalności K jest charakterystyczna dla substancji:

T_albo reprezentuje temperaturę środowiska.

Rozwiązane ćwiczenia

Ćwiczenie 1

Obliczyć średni współczynnik zmiany I z szacunkiem do X, Biorąc pod uwagę następujące wartości:

I₁ = 3; I₂ = 10; X₁ = 2; X₂ = 5

Rozwiązanie

Według wzoru:

Wartości podane w instrukcji zostały zastąpione, a operacja jest rozwiązana:

Ćwiczenie 2

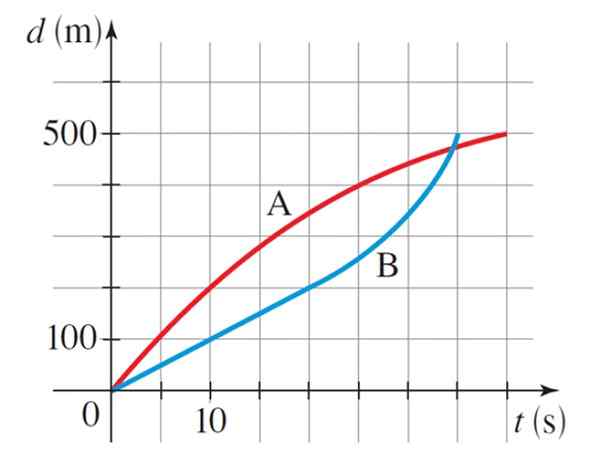
Wykres pokazuje odpowiednie krzywe odległości w porównaniu z czasem dwóch olimpijskich łyżwiarzy prędkości A i B, w modalności 500 metrów. Który wygrał wyścig? Jaka była średnia prędkość każdego łyżwiarza?

Rozwiązanie

Obserwując wykres, następuje, że skater B (niebieska krzywa) wygrał wyścig, ponieważ koncertował 500 m w 35 s, podczas gdy skater A (czerwona krzywa), zrobił to w 40 s.

Odpowiednie średnie prędkości wynosiły:

Bibliografia

1. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. Pod redakcją Douglas Figueroa (USB).
2. Glencoe Science. Szybkość zmian i nachylenia (2021). Odzyskane z: Glencoe.com.
3. Larson, r. (2012). Przedłużanie. 8. Wydanie. Cengage Learning.
4. Larson, r. (1986). Obliczenia z geometrią analityczną, 2. Wydanie. McGraw-Hill.
5. Stewart, J. (2011). Algebra uczelni, koncepcje i konteksty. Brooks/Cole.