Jakie użytkownika mają tabele i wykresy w raporcie?

Tabele i wykresy Są to narzędzia analityczne, których celem jest organizowanie, podsumowanie i komunikowanie informacji. Mają one ogromne znaczenie, zwłaszcza gdy w grę wchodzą dane liczbowe, ponieważ gdy są odpowiednio uporządkowane, ich interpretacja jest ułatwiona.

Postępowane są kwoty, które są obsługiwane Zmienne, które reprezentują atrybuty badanych wielkości. Mogą być numeryczne, takie jak miara lub wiek, a także jakościowe, takie jak płeć, kolor włosów lub inny.

Za pomocą tabel i wykresów ujawniają się wzorce, które umożliwiają określenie związku między różnymi zmiennymi. Bez odpowiedniej organizacji te wzorce te mogą być trudne do znalezienia, szczególnie gdy objętość danych jest duża.

Ze swojej strony wykres to rysunek, który pozwala czytelnikowi docenić istniejące wzory na pierwszy rzut oka.

Tabele służą nie tylko do zamówienia danych numerycznych, co będzie widać wkrótce. Służą również do podsumowania odpowiednich informacji na dany temat, takich jak listy z formułami, cechami, aplikacjami i przykładami, dlatego stanowią wspaniałe narzędzie do badań.

Stoły lub zdjęcia

Składają się z układu siatki z rzędami i kolumnami, należycie zidentyfikowane. W siatkach umieszczane są informacje, czy to numeryczne, tekstowe, czy kombinacja obu.

Tabela musi mieć tytuł, który go identyfikuje, a także różne wielkości i cechy, które zawiera. Jeśli są to wielkości numeryczne, zastosowana jednostka miary, na przykład długość należy określić w metrach, kilometrach, stopach, milach lub innej odpowiedniej jednostce.

Istnieje wiele rodzajów tabel, w tym, co następuje kilka przykładów, które ilustrują ich użycie:

Może ci służyć: hipoteza badań: co to jest, typy, przykłady

1. Opisowy stół lub tabela

Służy do podsumowania informacji na dany temat i ułatwienia badania. Jego konstrukcja jest bardzo zróżnicowana, w tym kolory, różne rodzaje liter, ikony i inne, zgodnie z projektantem obrazu.

Wiele procesorów tekstowych zawiera opcje projektowania tworzenia tabel i wstawienia ich do raportu lub dokumentu. Należy zauważyć, że zdjęcie lub tabela niekoniecznie zawiera wszystkie informacje na temat badanego tematu, ale te, które autor uważa za wygodne. Szczegóły można rozszerzyć w dalszej części raportu.

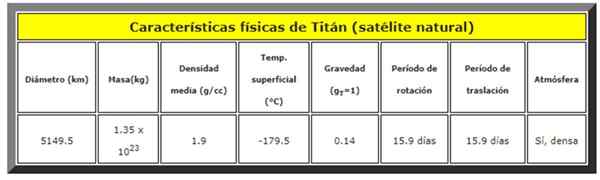
Jako przykład pokazano obraz o najwybitniejszych cechach fizycznych Tytana, naturalnego satelity planety Saturn. Niektórzy badacze twierdzą, że ten satelita spełnia warunki, które należy skolonizować przez ludzi w przyszłości.

2. Tabela porównawcza lub tabela

Jest to zasób używany do porównywania pojęć, pomysłów lub wielkości. Możesz dołączyć teksty z opisami i danymi liczbowymi. Poniżej znajduje się tabela porównawcza między pilny Thinker Inmanuel Kant Philosophical (1724-1804).

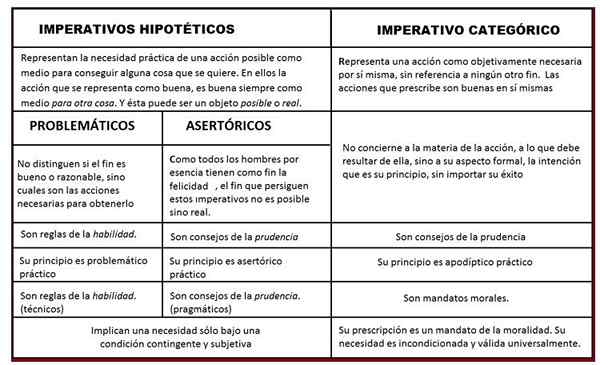Porównawcza tabela imperatywów Kanta. Źródło: Wikimedia Commons.

3. Tabela częstotliwości

W statystykach opisowych wygodne jest grupowanie danych na częstotliwościach, zasob.

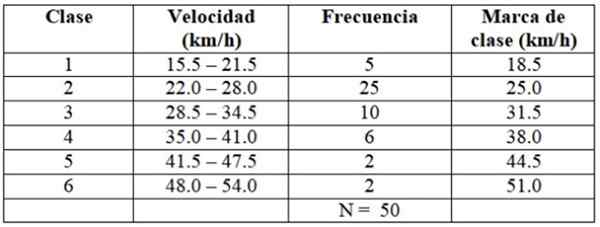
Poniższa tabela pokazuje prędkości pobrane przez radar, 50 samochodów, które przeszły przez aleję. 50 danych zorganizowano w 6 klasach, których odpowiednie częstotliwości i marki klasowe są pokazane. Ta tabela służy do obliczenia średniej, wariancji i odchylenia standardowego danych.

4. Tabela wartości funkcji

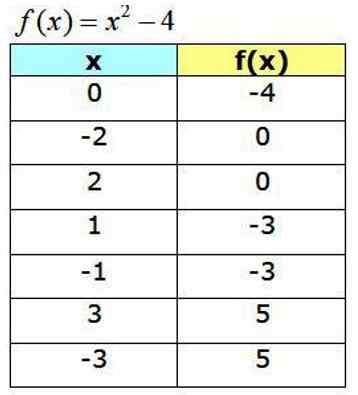
Pojęcie funkcji matematycznej jest kluczem do modelowania zarówno zjawisk natury, jak i najbardziej różnorodnych sytuacji. Funkcja zmienna X Można go reprezentować za pomocą tabeli wartości.

Może ci służyć: ośrodkowy układ nerwowy: funkcje, części, choroby

Następnie pokazano tabelę wartości dla funkcji f (x) = x²-4:

5. Tabela prawdy    

Tabele prawdy są używane w logice zdań, aby poznać wartość prawdy propozycji.

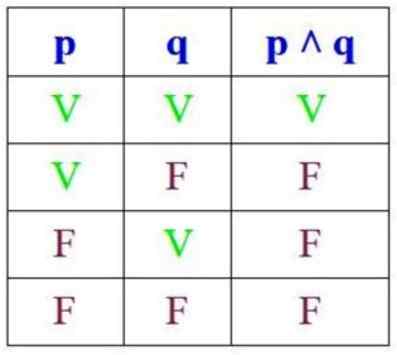
Tabela prawdy dla logicznej koniunkcji pojawia się natychmiast, która składa się z kombinacji dwóch prostych logicznych propozycji przez literę „y”, oznaczoną przez odwrócone „V”.

Kołustwo jest prawdziwe (v), gdy propozycje p i q są prawdziwe, jak w "Księżyc i Tytan to naturalne satelity”, W przeciwnym razie jest to fałszywe (f). Wartości prawdy kombinacji pokazano w tabeli:

Wykresy

Wykresy to zasoby wizualne, które ułatwiają analizę danych, poprzez ustalenie związku między zmiennymi. Są szeroko stosowane w takich obszarach, jak nauki podstawowe, statystyki, ekonomia i nauki społeczne.

Rodzaj wykresu zależy od charakteru reprezentowanych danych. Oto kilka przykładów wykresów częstego wyglądu:

1. Funkcje wykresy

Dla funkcji zmiennej wykres funkcji ma reprezentować uporządkowane pary (x, y) na płaszczyźnie kartezjańskiej. Składa się to z dwóch linii prostopadłych do siebie, jednej z nich poziomej, zwykle nazywanej osi x, a drugą pionową, zwaną osą i.

Dla funkcji f (x) = x²-4, którego tabela wartości pojawia się w poprzedniej sekcji, jego wykres jest łatwo narysowany za pomocą oprogramowania typu arkuszu kalkulacyjnego lub z internetowym programem graficznym.

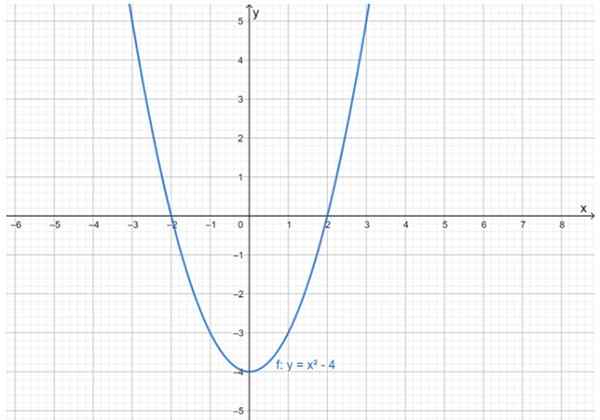Wykres funkcji kwadratowej. Źródło: f. Zapata przez Geogebra.

2. Bars Graphics

Zezwalaj na zmienne ilościowe i jakościowe, poprzez poziome lub pionowe słupki.

Może ci służyć: Charakterystyka kwadratu

Typowa piramida populacji jest dobrym przykładem wykresu słupkowego. W nim następuje coroczny podział populacji, według płci i rangi wiekowej.

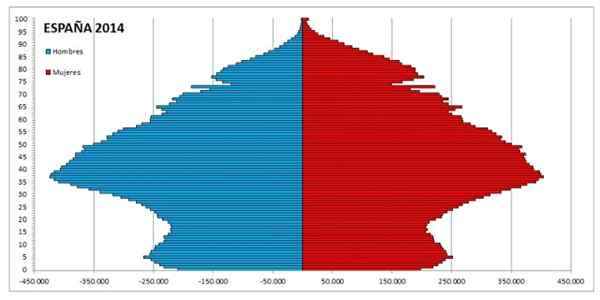Wykres barów z dystrybucją populacji hiszpańskiej na 2014. Źródło: Wikimedia Commons.

3. Wykresy sektorowe

Składają się z koła, które reprezentuje 100% danej zmiennej. Rozmiary sektorów kołowych są proporcjonalne do częstotliwości, z jaką pojawia się pewna charakterystyka lub atrybut. W poniższym przykładzie wykres jest pokazany przez sektory populacji angielskiej na świecie.

Obszar każdego sektora okrągłego jest proporcjonalny do ilości angloplanty w kraju i jest obliczany przez pomnożenie liczby PI, promień koła kwadratowego i amplitudę sektora mierzonego w stopniach, a następnie dzieląc wszystko przez 360º.

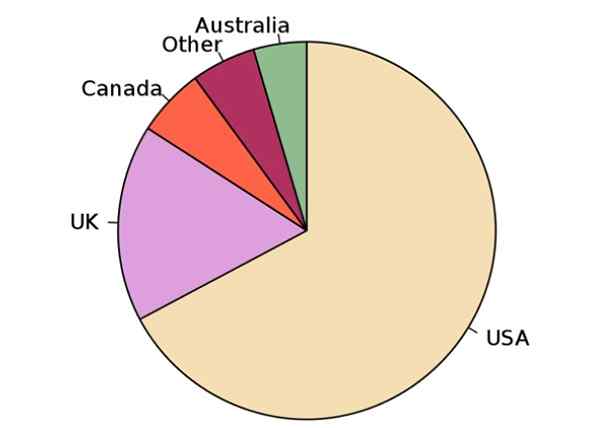Wykres według sektorów krajów Angloper. Źródło: Wikimedia Commons.

4. Wykres organizacji

Jest to graficzna reprezentacja hierarchicznej struktury, takiej jak firma lub organizacja. W ten sposób czytelnik raportu docenia dystrybucję głównych funkcji w tej organizacji.

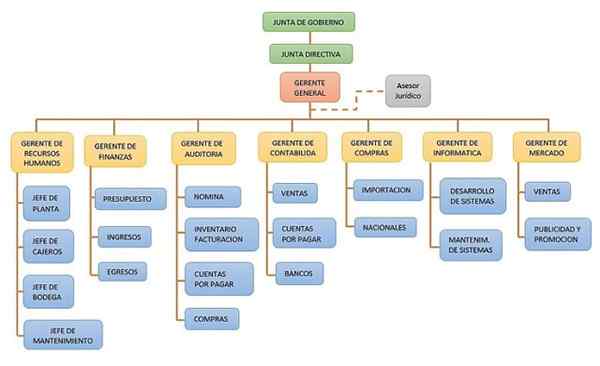Schemat organizacyjny. Źródło: Wikimedia Commons.

5. Wykresy ułamków

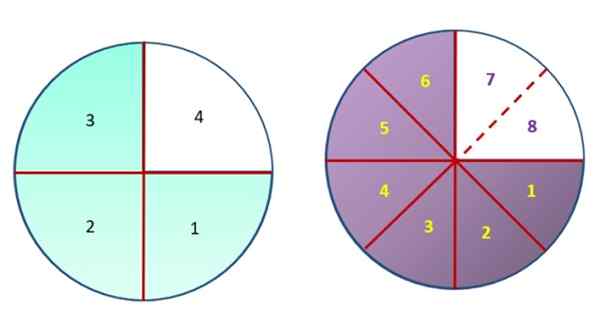
Służą do wizualizacji liczby ułamkowej. Na poniższym obrazie po lewej stronie okrąg jest podzielony na cztery równe części, tak że ułamek ¼ reprezentuje jedną z tych części.

Na lewym obrazie okrąg jest podzielony na osiem równych części, jeden z nich reprezentuje frakcję 1/8, a dwa z nich to 2/8, co odpowiada ¼.