Jaka jest prędkość liniowa? (Z rozwiązanymi ćwiczeniami)

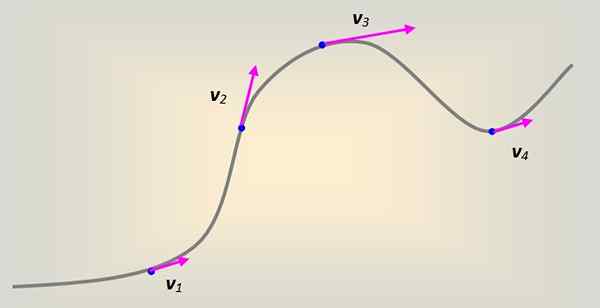
Prędkość liniowa Jest zdefiniowany jako ten, który jest zawsze styczny do trajektorii, a następnie cząsteczka, niezależnie od tego. Jeśli cząstka zawsze porusza się w trajektorii prostoliniowej, nie ma problemu z wyobrażeniem sobie, w jaki sposób wektor prędkości towarzyszy ta linia prosta.

Jednak ogólnie ruch jest przeprowadzany na krzywej arbitralnie. Każda część krzywej można modelować tak, jakby była częścią koła radiowego Do, które w każdym punkcie jest styczne do ścieżki.

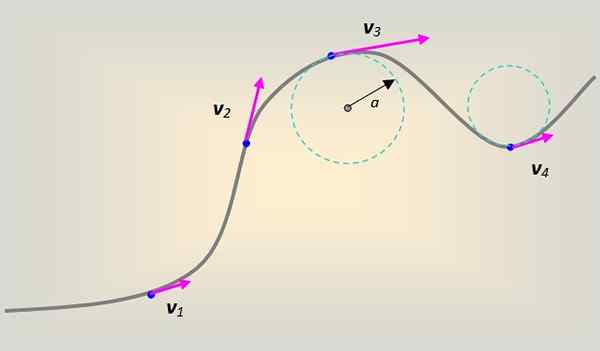Rysunek 1. Prędkość liniowa na telefonie komórkowym, który opisuje krzywoliniową trajektorię. Źródło: Self Made.

W takim przypadku prędkość liniowa towarzyszy stycznie i przez cały czas do krzywej w każdym punkcie.

Matematycznie natychmiastowa prędkość liniowa jest pochodną pozycji w odniesieniu do czasu. Być R wektor położenia cząstki w jednej chwili T, Następnie wyrażenie podaje prędkość liniową:

v = R'(T) = dR / dt

Oznacza to, że prędkość liniowa lub prędkość styczna, jak się nazywa, jest niczym innym jak zmianą pozycji w odniesieniu do czasu.

[TOC]

Prędkość liniowa w ruchu okrągłym

Kiedy ruch jest obwód, możemy w każdym punkcie przejść obok cząstki i zobaczyć, co stanie się w dwóch bardzo specjalnych kierunkach: jeden z nich jest tym, który zawsze wskazuje na środek. To jest adres promieniowy.

Innym ważnym kierunkiem jest ten, który ma miejsce na obwodzie, to jest adres styczny A prędkość liniowa zawsze ją ma.

Może ci służyć: ciśnienie manometryczne: wyjaśnienie, wzory, równania, przykłady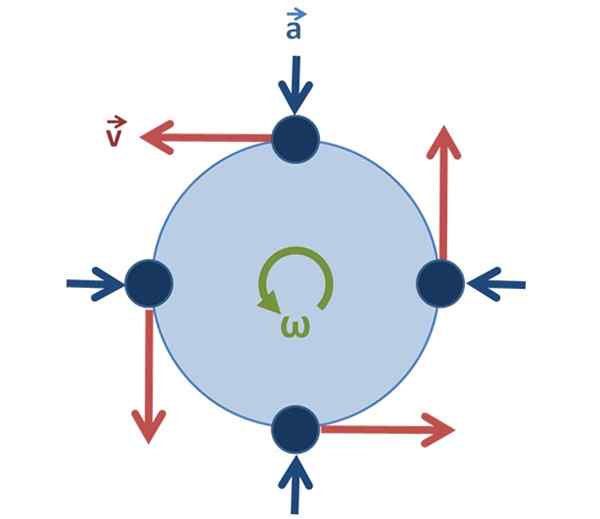Rysunek 2. Jednolity ruch kołowy: wektor prędkości zmienia kierunek i kierunek, gdy cząstka się obraca, ale jego wielkość jest taka sama. Źródło: Original by User: Brews_ohare, SVED przez użytkownika: Sjleg [CC BY-SA 3.0 (https: // creativeCommons.Org/licencje/by-sa/3.0)].

W przypadku jednolitego ruchu okrągłego jest ważne tak, pozostaje niezmienione.

W przypadku tego ruchu pozycja w funkcji czasu jest podana przez S (t), Gdzie S czy on jest Tourd Arc I T Już czas. W takim przypadku chwilowa prędkość wyraża wyrażenie V = ds/dt I jest stały.

Jeśli wielkość prędkości również różni się (wiemy już, że kierunek zawsze to robi, w przeciwnym razie telefon nie mógł się obrócić), stajemy w obliczu różnorodnego ruchu okrągłego, podczas którego mobilne oprócz obrotu może zatrzymać lub przyspieszyć.

Prędkość liniowa, prędkość kątowa i przyspieszenie dośrodkowe

Ruch cząstek można również zobaczyć z punktu widzenia Kąt zamiatania, Zamiast robić to z bramki podróży. W tym przypadku mówi się o prędkość kątowa. Do ruchu w kręgu radiowym R, Istnieje związek między łukiem (w radianach) a kątem:

S = r θ

Duszowanie w odniesieniu do obu stron:

ds/dt = r (dθ/dt)

Nazywając pochodną θ w odniesieniu do T Jak prędkość kątowa I oznaczając go grecką literą ω „omega”, masz ten związek:

v = ωR

Przyspieszenie dośrodkowe

Każdy ruch kołowy ma przyspieszenie dośrodkowe, To zawsze jest skierowane w kierunku środka obwodu. Uważa, że ​​prędkość zmienia się, aby poruszać się z cząsteczką, gdy się obraca.

Może ci służyć: krzywa kalibracji: po co to zrobić, jak to zrobić, przykłady

Przyspieszenie dośrodkowe Do_C albo Do_R Zawsze wskazuje na środek (patrz rysunek 2) i jest związany z prędkością liniową w ten sposób:

Do_C = v² /R

I z prędkością kątową jako:

Do_C = (ΩR)² /R = ω²R

W przypadku jednolitego ruchu okrągłego pozycja S (t) Jest to forma:

S (t) = so+ vt

Ponadto zróżnicowany ruch kołowy musi mieć element zwanego przyspieszenia Styczne przyspieszenie Do_T, To dotyczy zmiany wielkości prędkości liniowej. Tak Do_T  To jest stałe, Pozycja to:

S (t) = s_albo + v_alboT + ½ a_TT²

Z v_albo Jak początkowa prędkość.

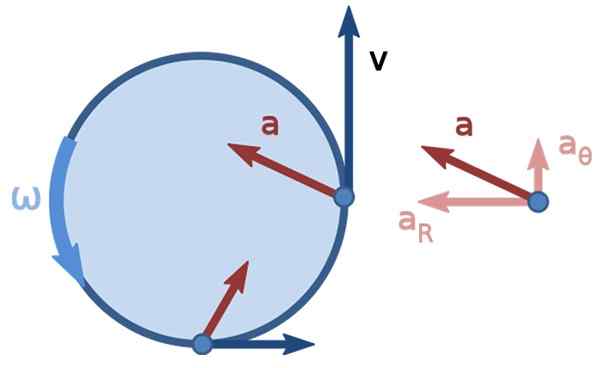Rysunek 3. Nieprzezroczysty ruch okrągły. Źródło: NonUniform_circular_motion.PNG: Brews Ohredorivative Prace: Kooning Jons [CC BY-SA 3.0 (https: // creativeCommons.Org/licencje/by-sa/3.0)].

Rozwiązane ćwiczenia liniowe

Rozwiązane ćwiczenia przyczyniają się do wyjaśnienia właściwego zastosowania podanych pojęć i równań.

-Ćwiczenie rozwiązane 1 

Owad porusza się na półkurku promienia r = 2 m, zaczynając od spoczynku w punkcie A podczas zwiększenia prędkości liniowej, z prędkością p m/s². Znajdź: a) Po tym, o której godzinie osiąga punkt B, B) Wektor prędkości liniowej w tym momencie, C) Przyspieszenie wektora w tym momencie.

Rysunek 4. Owad zaczyna się od A i dociera do B na półkolistej trajektorii. Ma prędkość liniową. Źródło: Self Made.

Rozwiązanie

a) Oświadczenie wskazuje, że przyspieszenie styczne jest stałe i jest warte π m/s², Wówczas ważne jest użycie równania do równomiernie zróżnicowanego ruchu:

S (t) = s_albo + v_alboT + ½ a_T.T²

Z s_albo = 0 i v_albo = 0:

S (t) = ½ a_T.T²

S = πR (Połowa długości obwodu)

T = (2. πR /Do_T) ^½ S = (2π.2 /π)^½S = 2 s

B) v (t) = v_albo + Do_T. T = 2π SM

Gdy w punkcie B liniowy wektor prędkości wskazuje w kierunku pionowym w dół w kierunku (-I):

Może ci służyć: jaka jest stała dielektryczna?

v (t) = 2π SM(-I)

c) Przyspieszenie styczne jest już miało, brakuje przyspieszenia dośrodkowego, aby mieć wektor prędkości Do:

Do_C = v² / R = (2π)² / 2 m/ s² = 2π² SM²

Do = a_C (-X) + a_T (-I) = 2π²(-X)+ π (-I) SM²

-Ćwiczenie rozwiązane 2

Cząstka obraca się w okręgu radiowym 2.90 m. W pewnym momencie jego przyspieszenie jest warte 1.05 m/s² w takim kierunku, który tworzy 32 z kierunkiem ruchu. Znajdź swoją liniową prędkość przy: a) w tej chwili, b) 2 sekundy później, zakładając, że przyspieszenie styczne jest stałe.

Rozwiązanie

a) Dyrekcja ruchu jest dokładnie adresem stycznym:

Do_T = 1.05 m/s² . cos 32º = 0.89 m/s² ; Do_C = 1.05 m/s² . Sen 32º = 0.56 m/s²

Prędkość wyczyściła Do_C = v² / R Jak:

v = (r.Do_C)^1/2  = 1.27 m/s

b) Równanie dla równomiernie zróżnicowanego ruchu jest ważne w następujący sposób: v = v_albo + Do_TT = 1.27 + 0.89 .2² m/s = 4.83 m/s

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill. 84-88.
2. Figueroa, zm. Seria fizyczna dla nauki i inżynierii. Tom 3. Wydanie. Kinematyka. 199-232.
3. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6^th… Ed Prentice Hall. 62-64.
4. Ruch względny. Odzyskane z: kursów.Lumenarning.com
5. Wilson, J. 2011. Fizyka 10. Edukacja Pearsona. 166-168.