Nieliniowe metody programowania i ćwiczenia

 Programowanie nieliniowe Jest to proces optymalizacji funkcji, która zależy od kilku zmiennych niezależnych, które z kolei podlegają ograniczeniom.

Jeśli jedno lub więcej ograniczeń lub funkcja w celu maksymalizacji lub zminimalizowania (nazywana Funkcja celu), nie jest wyrażany jako liniowa kombinacja zmiennych, więc istnieje problem programowania nieliniowego.

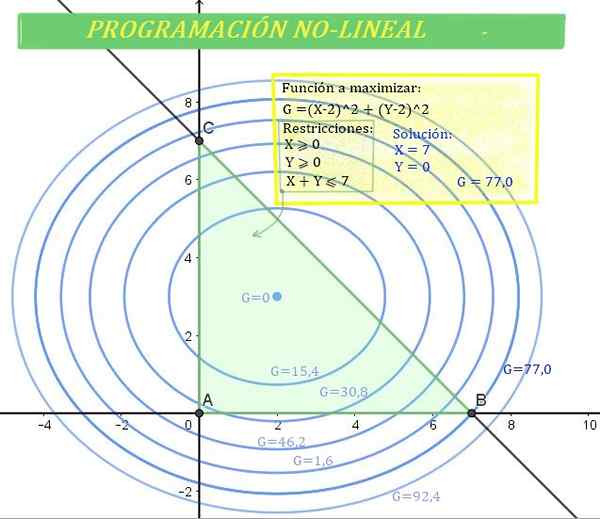
Rysunek 1. Problem z programowaniem nieliniowym (NLP). w której g jest funkcją (nieliniową) do optymalizacji w zielonym regionie, określonym przez ograniczenia. Źródło: f. Zapata.

I dlatego nie można zastosować procedur i metod programowania liniowego.

Na przykład nie można zastosować dobrze znanej metody Simplex, który ma zastosowanie tylko wtedy, gdy funkcja celu i ograniczenia są liniowe połączenie zmiennych problemu.

[TOC]

Metody programowania liniowego

Do programowania nieliniowego główne metody, które należy zastosować, to: 

1.- Metody graficzne.

2.- Mnożniki Lagrange w celu zbadania granicy regionu roztworu.

3.- Obliczanie gradientu w celu zbadania końców funkcji celu.

4.- Metoda zstępujących kroków, aby znaleźć punkty zero gradientu.

5.- Zmodyfikowana metoda mnożników Lagrange'a (ze stanem Karush-Kuhn-Tucker).

Przykład rozwiązania z metodą graficzną

Przykładem rozwiązania z metodą graficzną jest to, co można zobaczyć na rycinie 2:

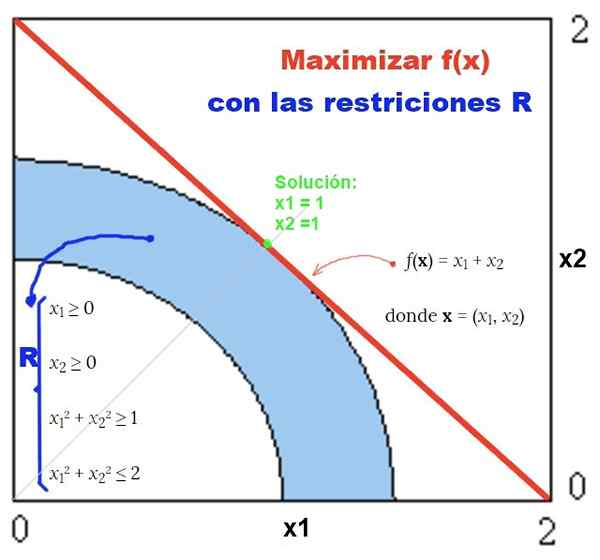Rysunek 2. Przykład problemu nieliniowego z ograniczeniami nieliniowymi i jego rozwiązaniem graficznym. Źródło: f. Zapata.

Ćwiczenia

- Ćwiczenie 1 (metoda graficzna)

Zysk z określonej firmy zależy od kwoty sprzedanej produktu X i kwoty sprzedanej produktu, a ponadto zysk jest określany przez następującą formułę:

Może ci służyć: sprzężony dwumian: jak jest rozwiązany, przykłady, ćwiczenia

G = 2 (x - 2)² + 3 (i - 3)²

Wiadomo, że kwoty x i y mają następujące ograniczenia:

X ≥0; Y≥0 i x + i ≤ 7

Określ wartości x i y, które wytwarzają maksymalny wzmocnienie.

Rysunek 3. Zysk firmy można modelować matematycznie, aby znaleźć maksymalny zysk przez programowanie nieliniowe. Źródło: Pixabay.

Rozwiązanie 

W tym problemie funkcja celu jest nieliniowa, podczas gdy nierówności, które określają ograniczenia. To jest problem Programowanie nieliniowe.

W przypadku rozwiązania tego problemu zostanie wybrana metoda graficzna.

Po pierwsze, zostanie określony obszar rozwiązania, który jest podany przez ograniczenia.

Jako x≥0; Y≥0, rozwiązaniem musi być wyszukiwanie w pierwszej ćwiartce płaszczyzny XY, ale jak dodatkowo należy spełnić, że x + y ≤ 7, roztwór znajduje się w dolnej półplanie linii x + y = 7 = 7.

Obszar roztworu jest przecięciem pierwszej ćwiartki z dolną półplaną linii, która powoduje powstanie trójkątnego regionu, w którym znajduje się roztwór. Jest taki sam, jak wskazano na rycinie 1.

Z drugiej strony, wzmocnienie g można również reprezentować w płaszczyźnie kartezjańskiej, ponieważ jego równanie dotyczy elipsy z centrum (2,3).

Elipsa pokazano na rycinie 1 dla kilku wartości g. Wyższa wartość g, większy wzrost.

Istnieją rozwiązania, które należą do regionu, ale nie dają maksymalnej wartości g, podczas gdy inne, takie jak g = 92.4, są poza zieloną strefą, to znaczy strefą roztworu.

Następnie maksymalna wartość g, taka, że ​​x e y należy do regionu roztworu, odpowiada: 

Może ci służyć: teoretyczne prawdopodobieństwo: jak to wyciągnąć, przykłady, ćwiczenia

G = 77 (maksymalny wzmocnienie), który występuje dla x = 7 e y = 0. 

Co ciekawe, maksymalny zysk występuje, gdy kwota sprzedaży produktu i jest nieważna, podczas gdy ilość produktu X osiąga największą możliwą wartość.

- Ćwiczenie 2 (Metoda analityczna: mnożniki Lagrange) 

Znajdź rozwiązanie (x, y), które sprawia, że ​​funkcja F (x, y) = x² + 2 i² być maksymalnie w regionie G (x, y) = x² + I² - 1 = 0.

Rozwiązanie

Jest to wyraźnie nieliniowy problem programowania, ponieważ zarówno funkcja celu f (x, y), jak i ograniczenie g (x, y) = 0, nie są liniową kombinacją zmiennych x i y.

Zostanie zastosowana metoda mnożnika Lagrange'a, która najpierw wymaga zdefiniowania funkcji Lagrange L (x, y, λ):

L (x, y, λ) = f (x, y) - λ g (x, y) = x² + 2 i² - λ (x² + I² - 1) 

Gdzie λ to parametr zwany Mnożnik Lagrange.

Aby określić ekstremalne wartości funkcji celu f, w regionie rozwiązania podanym przez ograniczenie g (x, y) = 0, następuje te kroki:

-Znajdź częściowe pochodne funkcji Lagrange'a, w odniesieniu do x, y, λ.

-Zero każdej pochodnej.

Tutaj sekwencja tych operacji:

1. ∂L/∂x = 2x - 2λx = 0
2. ∂L/∂y = 4y - 2λy = 0
3. ∂L/∂λ = -(x² + I² - 1) = 0

Możliwe rozwiązania systemowe

Możliwym rozwiązaniem tego systemu jest λ = 1, aby spełnić pierwsze równanie, w którym to przypadku y = 0, aby spełnić drugie.

To rozwiązanie implikuje, że x = 1 lub x = -1, tak aby trzecie równanie było spełnione. W ten sposób uzyskano dwa rozwiązania S1 i S2:

S1: (x = 1, y = 0)

S2: (x = -1, y = 0).

Inną alternatywą jest to, że λ = 2, aby drugie równanie zostało spełnione, niezależnie od wartości i.

Może ci służyć: limit fermat: to, co składa się i ćwiczenia rozwiązane

W tym przypadku jedynym sposobem na spełnienie pierwszego równania jest to, że x = 0. Biorąc pod uwagę trzecie równanie, istnieją tylko dwa możliwe rozwiązania, które nazwiemy S3 i S4:

S3: (x = 0, y = 1)

S4: (x = 0, y = -1)

Aby wiedzieć, które lub które z tych rozwiązań zmaksymalizuj funkcję celu, przejdź do wymiany w F (x, y):

S1: F (1, 0) = 1² + 2.0² = 1

S2: F (-1, 0) = (-1)² + 2.0² = 1

S3: F (0, 1) = 0² + 2.1² = 2

S4: F (0, -1) = 0² + dwadzieścia jeden)² = 2

Dochodzimy do wniosku, że rozwiązania, które maksymalizują f, gdy x i y należą do obwodu g (x, y) = 0 to s3 i s4.

Pary wartości (x = 0, y = 1) y (x = 0, y = -1) zmaksymalizują f (x, y) w regionie roztworu g (x, y) = 0.

- Ćwiczenie 3 (gradient zerowy)

Znajdź rozwiązania (x, y) dla funkcji celu:

f (x, y) = x² + 2 i²

Być maksymalnie w regionie G (x, y) = x² + I² - 1 ≤ 0.

Rozwiązanie

Ćwiczenie to jest podobne do ćwiczenia 2, ale region rozwiązania (lub ograniczenie) rozciąga się na wewnętrzny obszar obwodu g (x, y) = 0, to znaczy do okręgu g (x, y) ≤ 0. Obejmuje to obwód i jego obszar wewnętrzny.

Rozwiązanie graniczne zostało już określone w ćwiczeniu 2, ale konieczne jest zbadanie wewnętrznego regionu.

Aby to zrobić, gradient funkcji f (x, y) musi być obliczony i równy zerowi, aby poszukać ekstremalnych wartości w obszarze roztworu. Jest to równoważne obliczanie częściowych pochodnych F w odniesieniu do x i odpowiednio i wyrównanie zero:

∂f/∂x = 2 x = 0

∂f/∂y = 4 y = 0

Ten układ równań ma jedyne rozwiązanie (x = 0, y = 0), które należy do koła g (x, y) ≤ 0.

Zastępowanie tej wartości w funkcji F Wyniki:

f (0, 0) = 0

Podsumowując, maksymalna wartość, która zajmuje funkcję w regionie roztworu, wynosi 2 i występuje na granicy regionu rozwiązania, dla wartości (x = 0, y = 1) y (x = 0, y = -1).

 Bibliografia

1. Avriel, m. 2003. Programowanie nieliniowe. Publishing Dover.
2. Bazaraa. 1979. Programowanie nieliniowe. John Wiley & Sons.
3. Bertsekas, zm. 1999. Programowanie nieliniowe: wydanie 2. Atena Scientific.
4. Nocedal, J. 1999. Optymalizacja numeryczna. Springer-Verlag.
5. Wikipedia. Programowanie nieliniowe. Odzyskane z: jest.Wikipedia.com