Charakterystyka procesu politycznego, zastosowania i przykłady

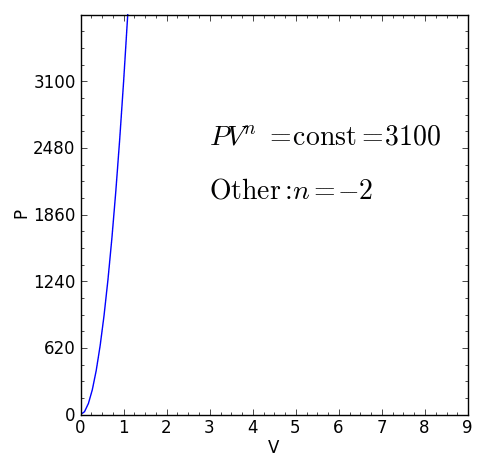
A Proces polityczny Jest to proces termodynamiczny, który występuje, gdy związek między ciśnieniem P i objętość V podane przez P.V^N Pozostaje stały. Wykładnik N Jest to liczba rzeczywista, ogólnie między zero a nieskończonością, ale w niektórych przypadkach może być ujemne.

Wartość N otrzymać nazwę Indeks polityczny I należy podkreślić, że podczas politropowego procesu termodynamicznego powiedział, że indeks musi zachować stałą wartość, w przeciwnym razie proces nie będzie uważany za politropowy.

Rysunek 1. Charakterystyczne równanie politropowego procesu termodynamicznego. Źródło: f. Zapata.

[TOC]

Charakterystyka procesów politropowych

Niektóre charakterystyczne przypadki procesów politropowych to: 

- Proces izotermiczny (w stałej temperaturze t), w którym wykładnik wynosi n = 1.

- Proces izobaryczny (stałe ciśnienie p), w tym przypadku n = 0.

- Proces izokoryczny (do stałej objętości V), dla którego n =+∞.

- Procesy adiabatyczne (do stałej entropii), w których wykładnik wynosi n = γ, będąc γ stałą adiabatyczną. Ta stała jest ilorazem między pojemnością cieplną przy stałym ciśnieniu CP podzielonym przez pojemność cieplną przy stałej objętości CV:

γ = CP/CV

- Każdy inny proces termodynamiczny, który nie jest żadnym z poprzednich przypadków. Ale przestrzegaj P.V^N = CTTE Z prawdziwym i stałym indeksem politropowym N Będzie to również proces politropowy.

Rysunek 2. Różne charakterystyczne przypadki politropowych procesów termodynamicznych. Źródło: Wikimedia Commons.

Aplikacje

Jednym z głównych zastosowań równania politropowego jest obliczenie pracy wykonanej przez zamknięty układ termodynamiczny, gdy przechodzi on ze stanu początkowego do innego końca w sposób quasi -statyczny, to znaczy po sukcesji stanów równowagi.

Praca w procesach politropowych dla różnych wartości n

Dla n ≠ 1

Prace mechaniczne W przeprowadzone przez zamknięty układ termodynamiczny jest obliczany na podstawie wyrażenia:

W = ∫p.DV

Może ci służyć: diamagnetyzm: materiały, aplikacje, przykłady

Gdzie p jest ciśnieniem i v objętość.

Podobnie jak w przypadku procesu politropowego, związek między ciśnieniem a objętością wynosi:

P.V ^N = stała = c

Oczyszczanie P poprzedniego wyrażenia, aby zastąpić go w wyrażeniu pracy:

P = c /V ^N

Masz pracę mechaniczną podczas procesu politropowego, który rozpoczyna się w stanie początkowym 1, a kończy w stanie końcowym 2. Wszystko to pojawia się w następującym wyrażeniu:

Jeśli n ≠ 1, masz:

Ponadto, ponieważ stany początkowe i końcowe są dobrze zdefiniowane, stała jest również określana przez następujące wyrażenie:

C = p₁ V₁^N = P₂ V₂^N

Zastępowanie wartości stały w ekspresji pracy jest uzyskiwane:

W = (p₂ V₂ - P₁ V₁)/(1-N)

W przypadku, gdy substancja robocza można modelować jako gaz idealny, ma następujące równanie stanu:

P.V = m.R.T

Gdzie m jest liczbą moli idealnego gazu, a r jest uniwersalną stałą gazów.

Dla idealnego gazu, który następuje po politropowym z indeksem politropii inną od urządzenia i który przechodzi ze stanu o początkowej temperaturze t₁ do innego stanu o temperaturze t₂ Prace wykonane jest następujący formuła:

W = m r (t₂ - T₁)/(1-N)

Dla n → ∞

Zgodnie z wzorem dla prac uzyskanych w poprzednim rozdziale praca politropowego z n = ∞ jest zerowa, ponieważ ekspresja pracy jest podzielona między nieskończoność, a zatem wynik ma tendencję do zera.

Innym sposobem osiągnięcia tego wyniku jest rozpoczęcie od relacji P₁ V₁^N = P₂ V₂^N, które można przepisać w następujący sposób:

(P₁/P₂) = (V₂/V1)^N

Biorąc korzeń n-Thicker w każdym otrzymanym członku:

(V₂/V1) = (p₁/P₂)^(1/n)

W przypadku n → ∞, musisz (v₂/V1) = 1, co oznacza, że:

Może ci służyć: Ceded Heat: Formule, jak je obliczyć i rozwiązane ćwiczenia

V₂ = V₁

Oznacza to, że objętość nie zmienia się w procesie politropowym z n → ∞. Dlatego różnica objętości DV w całce pracy mechanicznej wynosi 0. Tego rodzaju procesy politropowe są również znane jako procesy izokoryczny, o Procesy przy stałej objętości.

Dla n = 1

Znowu mamy wyraz pracy:

W = ∫p DV

W przypadku procesu politropowego o n = 1 związek między ciśnieniem a objętością wynosi:

P V = stała = C

Oczyszczając P poprzedniego wyrażenia i zastępując, wykonano pracę, aby przejść ze stanu początkowego 1 do stanu końcowego 2:

W = ∫12p dv = ctte ∫12 v^( - 1) dv = ctte (ln (v2) - ln (v1))

To jest do powiedzenia:

W = c ln (v₂/V₁).

Ponieważ stany początkowe i końcowe są dobrze ustalone, podobnie jak CTTE. To jest do powiedzenia:

C = p₁ V₁ = P₂ V₂

Wreszcie, dostępne są następujące przydatne wyrażenia, aby znaleźć pracę mechaniczną politropowego zamkniętego układu, w którym n = 1.

W = p₁ V₁ LN (v₂/V₁) = P₂ V₂ LN (v₂/V₁)

Jeśli składa się substancja robocza M Mole idealnego gazu, wówczas można zastosować równanie gazowe idealne: p v = m.R.T.

W tym przypadku, jak P.V₁ = CTTE, proces politropowy o n = 1 jest procesem w stałej temperaturze t (izotermicznej), dzięki czemu można uzyskać następujące wyrażenia pracy:

W = m r t₁ LN (v₂/V₁) = m r t₂ LN (v₂/V₁)

Rysunek 3. Topnienie Carambana, przykład procesu izotermicznego. Źródło: Pixabay.

Przykłady procesów politropowych

- Przykład 1

Załóżmy cylinder z ruchomym tłokiem pełnym z kilogramem powietrza. Początkowo powietrze zajmuje tom v₁= 0,2 m³ pod ciśnieniem p₁= 400 kPa. Proces politropowy następuje n = γ = 1,4, którego stan końcowy ma ciśnienie p₂ = 100 kPa. Określić pracę wykonaną w powietrzu na tłoku.

Rozwiązanie

Gdy wskaźnik politropii jest równy stałej adiabatycznej, istnieje proces, w którym substancja robocza (powietrze) nie wymienia ciepła z środowiskiem, a zatem nie zmienia entropii.

Może ci służyć: trzecie prawo termodynamiki: wzory, równania, przykłady

W przypadku powietrza idealnego gazu diatomic masz:

γ = CP/CV, z CP = (7/2) R i CV = (5/2) R

Więc:

γ = 7/5 = 1,4

Korzystając z wyrażenia procesu politropowego, można określić końcową objętość powietrza:

V₂ = [Str₂ V₁^1.4)/P₂]^(1/1.4) = 0,54 m³.

Teraz istnieją warunki do zastosowania wzoru roboczego wykonanego w procesie politropowym dla n ≠ 1 uzyskane powyżej:

W = (p₂ V₂ - P1 V1)/(1-N)

Zastąpienie odpowiednich wartości to:

W = (100 kPa 0,54 m³ - 400 kPa 0,2 m³)/(1 - 1,4) = 65,4 kJ

- Przykład 2

Załóż ten sam cylinder z przykładu 1, z ruchomym tłokiem pełnym z kilogramem powietrza. Początkowo powietrze zajmuje objętość V1 = 0,2 m³ Pod ciśnieniem P1 = 400 kPa. Ale w przeciwieństwie do poprzedniego przypadku powietrze rozszerza się izotermicznie, aby osiągnąć ciśnienie końcowe P2 = 100 kPa. Określić pracę wykonaną w powietrzu na tłoku.

Rozwiązanie

Jak wcześniej widać, procesy izotermiczne są procesami politropowymi o indeksie n = 1, więc jest spełnione, że:

P1 V1 = P2 V2

W ten sposób ostateczny objętość można łatwo odłączyć, aby uzyskać:

V2 = 0,8 m³

Następnie użycie wyrażenia pracy wcześniej uzyskanej dla przypadku n = 1 musisz pracować w powietrzu na tłoku w tym procesie:

W = P1 V1 LN (V2/V1) = 400000 PA × 0,2 M³ LN (0,8/0,2) = 110,9 kJ.  

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
2. Cengel i. 2012. Termodynamika. 7. edycja. McGraw Hill.
3. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 4. Płyny i termodynamika. Pod redakcją Douglas Figueroa (USB).
4. López, c. Pierwsze prawo termodynamiki. Odzyskane z: cultureacientafica.com.
5. Knight, r. 2017. Fizyka dla naukowców i inżynierii: podejście strategiczne. osoba.
6. Serway, r., Vulle, c. 2011. Podstawy fizyki. 9na ed. Cengage Learning.
7. Uniwersytet Sevilla. Maszyny termiczne. Odzyskany z: Laplace.nas.Jest.
8. Wikiwand. Proces polityczny. Odzyskane z: Wikiwand.com.