Heksagonalny pryzmat

Wyjaśniamy, czym jest heksagonalny pryzmat, jego cechy, elementy, obszar, wierzchołki, krawędzie i jak je obliczyć.

Co to jest heksagonalny pryzmat?

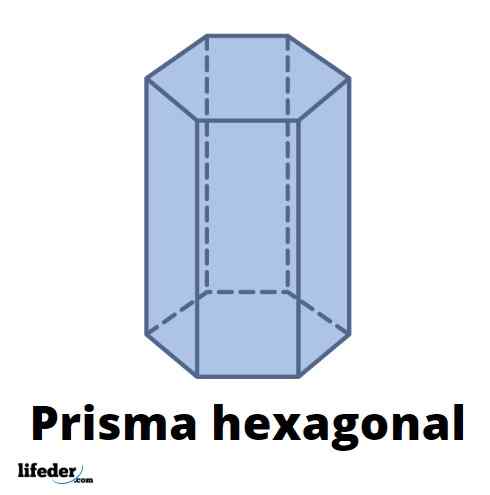
A Heksagonalny pryzmat Jest to trójwymiarowe ciało złożone z dwóch kształtów sześciokąta i boków w kształcie prostokąta lub równoległoboku. Można go znaleźć w naturze, w krystalicznej strukturze minerałów, takich jak beryl, grafit, cynk i lit,.

Elementy heksagonalnego pryzmatu to podstawa, twarz, krawędź, wysokość, wierzchołek, radio i apothem. Z nich można obliczyć obszary i objętości.

Górna postać pokazuje heksagonalny pryzmat z prostokątnymi twarzami bocznymi; to jest do powiedzenia, Prosty heksagonalny pryzmat. Sześciokąt baz są regularne, to znaczy ich wewnętrzne strony i kąty są takie same. Jednak heksagonalne twarze pryzmatyczne mogą być nieregularnymi sześciokątami.

Charakterystyka heksagonalnego pryzmatu

1- heksagonalny pryzmat jest trójwymiarową postacią z heksagonalnymi bazami.

2- Istnieje wiele różnych obiektów, które reagują na tę definicję, a jednak są zupełnie inne.

W poniższej liczbie istnieje wiele heksagonalnych pryzmatów: po lewej prostej heksagonalnej pryzmatu zwykłych twarzy, po prawej i w dół dwóch sześciokątnych pryzmatów nieregularnych twarzy. Sześciokąt u podstawy pryzmatu poniżej ma szczególną szczególność wklęsły, Co oznacza, że ​​niektóre z jego wewnętrznych kąty są większe niż 180 °.

Różnorodność heksagonalnych pryzmatów. Źródło: Wikimedia Commons.

Z drugiej strony, sześciokątne podstawy pryzmatów powyżej to wielokąt wypukły: Wszystkie kąty wewnętrzne mierzą mniej niż 180 °.

Elementy heksagonalne pryzmatyczne

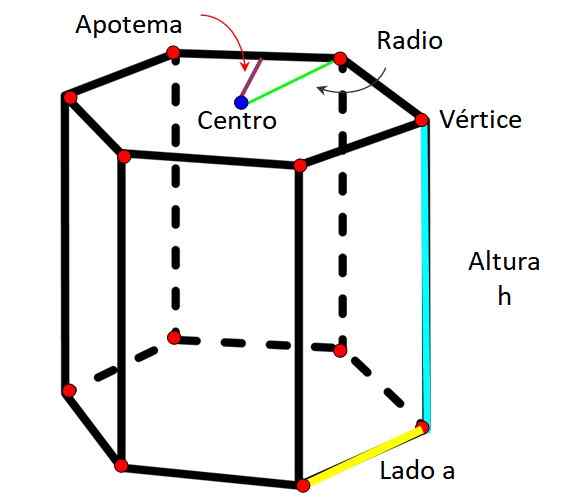Elementy heksagonalne pryzmatyczne. Źródło: f. Zapata

Jak każdy pryzmat, heksagonalny pryzmat charakteryzuje się posiadaniem następujących elementów:

Może ci służyć: odwrotność multiplikatywna: wyjaśnienie, przykłady, rozwiązane ćwiczenia

-Bazy: w liczbie dwóch (2), w postaci sześciokąta i przystających, to znaczy równej miary. Heksagonalne twarze mogą być regularne lub nieregularne.

-Twarze: Heksagonalny pryzmat ma ogółem osiem (8) twarzy, które można policzyć za pomocą rysunku 1. Z 8 twarzy dwie (2) to podstawy, a sześć (6) jest bocznych.

-Krawędź: To segment łączy dwie bazy lub dwie strony pryzmatu.

-Wysokość: Jest to odległość między dwiema twarzami pryzmatu. Zbiega się z długością krawędzi w przypadku prostego pryzmatu.

-Wierzchołek: Wspólny punkt między bazą i dwiema stronami bocznymi.

Jeśli podstawy pryzmatu są regularne, symetria postaci pozwala zdefiniować dodatkowe elementy zwykłej strony sześciokątnej Do.

-Radio: Jest to odległość mierzona od środka sześciokąta i dowolnego wierzchołka.

-Apothem: To segment przechodzi od środka sześciokątnej twarzy na środek jednej strony.

Za pomocą tych elementów obliczane są obszary i objętości, jak zobaczymy później.

Formuły

Istnieje wiele formuł związanych z heksagonalnym pryzmatem. Służą do obliczania obszaru ich podstaw i twarzy, jego objętości i innych ważnych cech. Przydatne są obszary regularnego sześciokąta, nieregularnego sześciokąta i równoległoboku, a także obwodów.

Obwód płaskiej figury

Jest miarą jego konturu, który w przypadku wielokąta, takiego jak heksagon, jest sumą jego boków. Jeśli sześciokąt jest regularny na boki Do, Istnieje formuła obwodu P:

P = 6.Do

Regularny obszar sześciokąta

Zadzwońmy do ALS i L_DO Na długości Apotheme. Obszar jest podany przez:

Może ci służyć: Dane bez grupy: Przykłady i ćwiczenia rozwiązane

A = p. L_DO/2 = 6a. L_DO/2

Gdzie P jest obwodem figury.

W zależności od wielkości strony Do, Obszar można również obliczyć przez:

A = 2.5981.Do²

Nieregularny obszar sześciokąta

Nie ma konkretnej formuły, ponieważ zależy to od rozmieszczenia boków, ale sześciokąt można podzielić na trójkąty, obliczyć obszar każdego z nich i dodać.

Inną metodą znalezienia obszaru jest determinanty Gaussa, dla których konieczne jest znanie współrzędnych wierzchołków sześciokątnych.

Obszar równoległobramowy

A = podstawa x wysokość

Tak Do jest podstawą i H To wysokość, obszar to:

A = a.H

Sześciokątny obszar pryzmatu

Jest to suma obszarów baz -dwa heksagony -i obszary twarzy -6 prostokąty lub równoległoboki-.

Regularny sześciokątny obszar pryzmatu

Jeśli heksagonalny pryzmat ma podstawy w postaci zwykłych heksagonów, a krawędzie boczne są prostopadłe do tych baz, jego obszar jest podany przez sumę:

A = 2 x 2.5981.Do² + 6th.H

Gdzie Do To jest strona sześciokątna i H Jest to wysokość pryzmatu.

Nieregularny i prosty heksagonalny obszar pryzmatu

Jeśli podstawy są nieregularnymi heksagonami, obszar oblicza się przez:

A = 2a_baza  + P.H

Gdzie:

-DO_baza Jest to nieregularny sześciokątny obszar podstawowy.

-P jest obwodem podstawy.

-H to wysokość pryzmatu

Wierzchołki

Każda sześciokątna twarz ma 6 zakrętów lub wierzchołków, co daje w sumie 12 wierzchołków dla heksagonalnego pryzmatu.

Krawędzie

Istnieje formuła znalezienia liczby krawędzi pryzmatu. Został odkryty przez wielkiego matematyka Leonharda Eulera (1707-1783) i nazywa się Twierdzenie Eulera dla Polyhedros. Mówi więc:

Może ci służyć: rozumowanie algebraiczne

Jeśli C jest liczbą twarzy i ilości Vértices V i całkowitych krawędzi. To prawda, że:

C+V = a+2

Ilości dla heksagonalnego pryzmatu wynoszą: c = 8 i v = 12. Dlatego jest:

A = C + V - 2 = 8 + 12-2 = 18

Tom

Objętość V każdego pryzmatu, zarówno prostego lub ukośnego, regularnych lub nieregularnych twarzy, jest podana przez:

V = powierzchnia podstawy x wysokość

Dlatego będziemy potrzebować formuł dla obszaru, który widzieliśmy wcześniej.

Na przykład, dla prostego heksagonalnego pryzmatu, którego podstawami są zwykłe sześciokąt, tom jest podany przez:

V = 2.5981.Do².H

Bibliografia

1. Odniesienie do otwartego matematyki. Obszar wielokąta. Odzyskane z: Mathpenref.com.
2. Wikipedia. Pryzmat. Odzyskane z: jest.Wikipedia.com.