Zasadnicza formuła, demonstracja, aplikacje

On Zasada Archimedesa Mówi, że całkowicie lub częściowo zanurzone ciało otrzymuje powołaną siłę pionową naciskać, co odpowiada ciężarowi objętości cieczy przemieszanej przez ciało. 

Niektóre obiekty unoszą się w wodzie, inne tonie, a niektóre częściowo zanurzają się. Zatopić piłkę plażową, konieczne jest podjęcie wysiłku, ponieważ siła ta jest natychmiast postrzegana, która próbuje jej zwrócić na powierzchnię. Zamiast tego metalowa kula szybko tonie. 

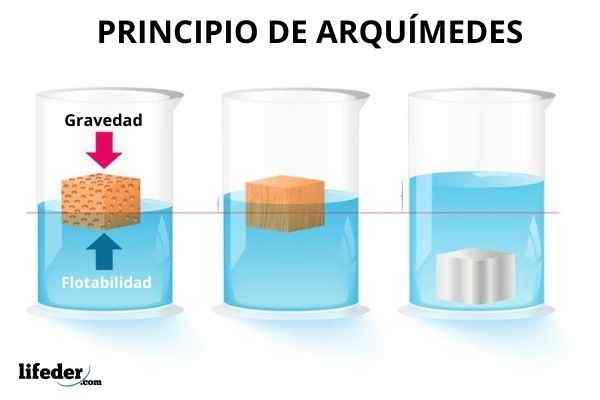
Z drugiej strony, zanurzone obiekty wydają się lżejsze, dlatego istnieje siła wywierana przez płyn przeciwny wagi. Ale nie zawsze możesz w ogóle zrekompensować grawitację. I chociaż jest to bardziej widoczne w przypadku wody, gazy są również w stanie wytworzyć tę siłę na zanurzonych obiektach.

[TOC]

Historia

Archimedes of Syracuse (287-212 A. C.) To był ten, który musiał odkryć tę zasadę, będąc jednym z największych naukowców w historii. Mówią, że król Hierón II z Syracuse wysłał złota do wyprodukowania nowej korony, za którą wręczył mu pewną ilość złota.

Archimedes

Kiedy król otrzymał nową koronę, miał odpowiednią wagę, ale podejrzewał, że złotnik go zdradził, dodając srebro zamiast złota. Jak mogłem to sprawdzić bez niszczenia korony?

Hierón nazwał Archimedes, którego sława uczonego była dobrze znana, aby pomóc mu rozwiązać problem. Legenda potwierdza, że ​​Archimedes zanurzył się w wannie, gdy znalazł odpowiedź i, taka była jego emocje, że pobiegł nago ulicami Syracuse, aby poszukać króla krzyczącego „Eureka”, co oznacza „znalazłem to”.

https: // giphy.com/gifs/stito3echtlnbvliz3

Co znaleźli Archimedes? Cóż, podczas biorąc łazienkę poziom wody w wannie, kiedy wszedł, co oznacza, że ​​zanurzone ciało wypiera pewną objętość płynu.

A jeśli zanurzyłem koronę w wodzie, musiała również poruszyć pewną objętość wody, jeśli korona została wykonana ze złota i innego, jeśli została wykonana ze stopu z srebrem.

Zasada archimedesa formuła

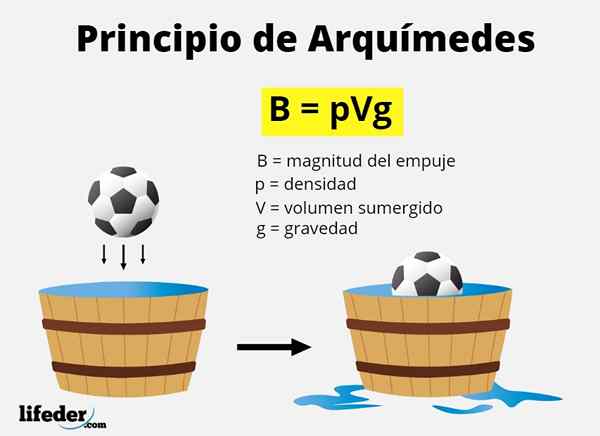
Siły promocyjne, o których mowa w zasadzie Archimedesa, jest znana jako naciskać hydrostatyczny albo siła flotacyjna I, jak powiedzieliśmy, jest to równoważne ciężarowi objętości płynu przemieszczonego przez ciało po zanurzeniu.

Przesunięty wolumin jest równoważny objętości zanurzonego obiektu, całkowicie lub częściowo. Ponieważ waga czegokolwiek jest Mg, A masa płynu jest Gęstość x objętość, Zaprzeczając, jak B do wielkości ciągu, matematycznie musi:

B = m_biegły x g = gęstość płynu x zanurzona objętość x grawitacja

B = ρ_biegły x v_zanurzony x g

Gdzie grecka litera ρ („rho”) oznacza gęstość.

Pozorna waga

Waga obiektów jest obliczana przez dobrze znane wyrażenie Mg, Jednak sprawy są lżejsze, gdy są zanurzone w wodzie. 

On pozorna waga obiektu jest to, co ma, gdy jest zanurzony w wodzie lub w innym cieczy i wiedząc o tym, możesz uzyskać objętość nieregularnego obiektu, takiego jak korona króla Hieróna.

Może ci służyć: 13 przykładów pierwszego prawa Newtona w prawdziwym życiu

Aby to zrobić, jest całkowicie zanurzony w wodzie i podlega linę przymocowaną do dynamometr -instrument dostarczany ze sprężyną, która służy do pomiaru sił-. Im większa waga obiektu, tym większe wydłużenie sprężyny, które jest mierzone w skali dostarczonej w urządzeniu.

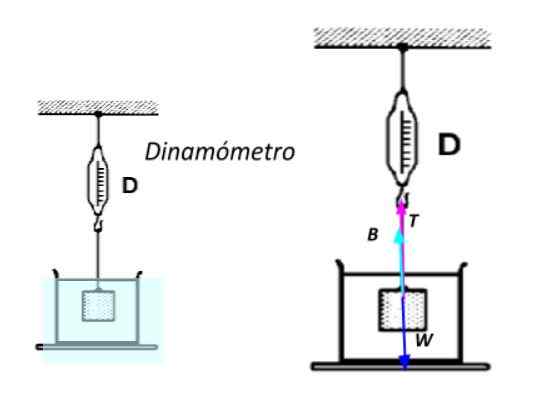Widoczna waga zanurzonego obiektu. Źródło: Przygotowane przez F. Zapata.

Zastosowanie drugiego prawa Newtona, wiedząc, że obiekt jest w spoczynku:

Σf_I = B + t - w = 0

Pozorna waga w_Do Jest to równoważne napięciem na linii:

T = w_Do

W_Do = mg - ρ_biegły . V. G

Jeśli wymagany jest zanurzony tom V, jest on wyczyszczony jako:

V = (w - w_Do ) / ρ_biegły  . G

Demonstracja

https: // giphy.com/gifs/mcphppgtnpbhl4cgaq

Kiedy ciało zanurza się, ciąg jest siłą wynikającą ze wszystkich sił wywieranych na ciało przez ciśnienie spowodowane otaczającym płynem:

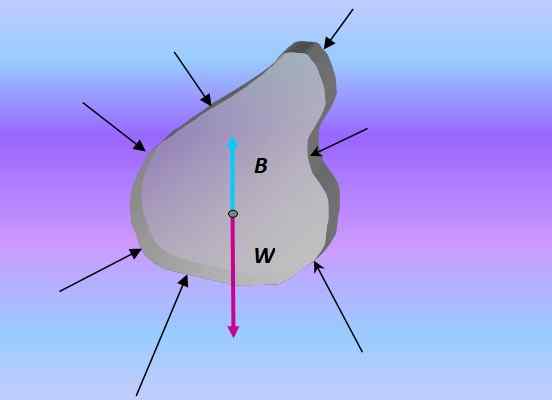Bezpłatny schemat ciała zanurzonego obiektu. Źródło: Przygotowane przez F. Zapata.

Ciśnienie i głębokość

Ponieważ ciśnienie wzrasta wraz z głębokością, wynik tych sił jest zawsze kierowany pionowo w górę. Dlatego zasada Archimedesa jest konsekwencją podstawowego twierdzenia hydrostatycznego, które wiąże ciśnienie p wywierane przez płyn o głębokości z Jak:

P = ρ.G.z

Siły na statycznym płynie równowagi

Aby zademonstrować zasadę Archimedesa, w spoczynku niewielka cylindryczna część spoczynkową jest analiza wywieranych na nią sił, jak pokazano na poniższym rysunku. Siły na zakrzywionej powierzchni cylindra są anulowane. 

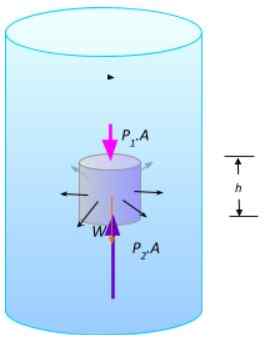Część płynu w równowadze. Źródło: Przygotowane przez F. Zapata.

Wielkości sił pionowych są F₁ = P₁.A i F₂ = P2.A, jest waga W. Ponieważ płyn jest w równowadze, suma sił należy anulować:

∑f_I = P₂.A- p₁.A- W = 0

P₂.A- p₁.A = w

Ponieważ ciąg kompensuje wagę, ponieważ część płynu jest w spoczynku, następnie:

B = p₂.A- p₁.A = w

Z tego wyrażenia wynika, że ​​ciąg jest spowodowany różnicą ciśnienia między górną powierzchnią cylindra a dolną. Jak W = mg = ρbiegły. V. G, Musisz:

B = ρ_biegły. V_zanurzony. G

Co jest dokładnie wyrażeniem pędu wymienionego w poprzednim rozdziale.

Zastosowania Zasady Archimedes

Balony, które unoszą się: zasada Archimedes w akcji

Zasada Archimedesa pojawia się w wielu praktycznych zastosowaniach, wśród których możemy wymienić:

- Balon aerostatyczny. Które dzięki średniej gęstości mniejszej niż otaczającego powietrza unosi się w nim z powodu siły ciągu.

- Związki. Hełm statku jest cięższy niż woda. Ale jeśli kadłub jest rozpatrywany plus powietrze w środku, iloraz między masą całkowitą a objętością jest mniejszy niż w przypadku wody i to jest powód, dla którego statki unoszą się.

- Kamizelki ratunkowe. Po zbudowaniu lekkich i porowatych materiałów są w stanie unosić się, ponieważ stosunek masowy jest mniejszy niż w przypadku wody.

- Pływający w celu zamknięcia kranu napełniającego zbiornika na wodę. Jest to kula pełna powietrza o dużej objętości, która unosi się nad wodą, która powoduje siłę ciągu - pomnożoną przez efekt dźwigni - zamyka nasadkę kranu napełniającego zbiornika wody, gdy osiągnie całkowitą liczbę poziomów.

Może ci służyć: fale jednoznaczne: wyrażenie matematyczne i przykłady

Przykłady

Przykład 1

Legenda mówi, że król Hierón dał złotowi pewną ilość złota, aby stworzyć koronę, ale nieufny monarcha pomyślał, że złotnik mógł oszukać, umieszczając mniej cennego metalu w koronie niż korona. Ale skąd mogę wiedzieć bez niszczenia korony? 

Król zlecił Archimedesa i to, szukając rozwiązania, odkrył swoją słynną zasadę.

Załóżmy, że korona waży 2,10 kg-F w powietrzu i 1,95 kg-F, gdy jest całkowicie zanurzona w wodzie. W takim przypadku nie ma oszustwa?

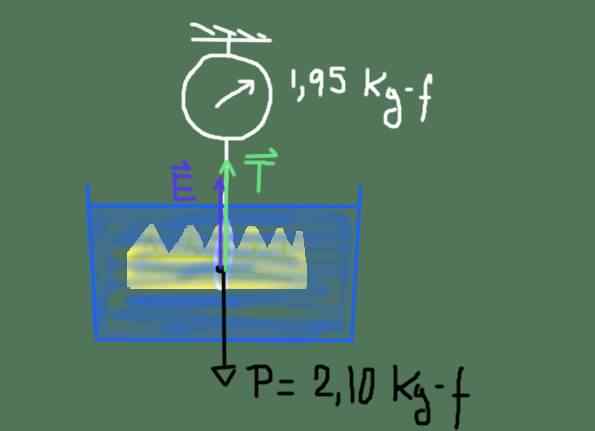Schemat ciała Króla Herona Wolne ciało. Źródło: Przygotowane przez F. Zapata

Schemat sił pokazano na poprzedniej rysunku. Te siły to: waga P korony, ciąg I i napięcie T liny, która wisi na skali.

P = 2,10 kg-f i t = 1,95 kg-f jest znane, konieczne jest określenie wielkości ciągu I:

T + e = p ⇒ e = p - t = (2,10 - 1,95) kg -f = 0,15 kg -f

Z drugiej strony, zgodnie z zasadą Archimedesa, ciąg jest równoważny ciężarowi eksmitowanej wody przestrzeni zajmowanej przez koronę, to znaczy gęstość wody przez objętość korony z powodu przyspieszenia grawitacji :

E = ρ_woda⋅V⋅G = 1000 kg/m^3 ⋅ v ⋅ 9,8 m/s^2 = 0,15 kg ⋅ 9,8 m/s^2

Gdzie można obliczyć objętość korony:

V = 0,15 kg / 1000 kg / m^3 = 0,00015 m^3

Gęstość korony jest ilorazem między masą korony z wody a jej objętością:

Gęstość korony = 2,10 kg / 0,00015 m^3 = 14000 kg / m^3

Gęstość czystego złota można określić na podstawie podobnej procedury, a wynik to 19300 kg/m^3.

Porównując dwie gęstości, oczywiste jest, że korona nie jest czystym złotem! 

Przykład 2 

Na podstawie danych i wyniku przykładu 1 możliwe jest ustalenie, ile złota zostało skradzione przez Goldsmith w przypadku, że część złota została zastąpiona srebrem, która ma gęstość 10500 kg/m^3 3.

Nazwimy ρc do gęstości korony, ρo do gęstości złota i ρ_P do gęstości srebra.

Całkowita masa korony to:

M = ρc⋅v = ρo⋅vo + ρ_P⋅VP

Całkowita objętość korony to objętość srebra plus objętość złota:

V = vo + vp ⇒ vp = v - vo

Zastąpienie w równaniu masowym:

ρc⋅v = ρo⋅vo + ρ_P⋅ (v - vo) ⇒ (ρo - ρ_P) Vo = (ρc - ρ_P) V

To znaczy, że objętość złota, która zawiera koronę całkowitej objętości V to:

VO = v⋅ (ρc - ρ_P)/(ρo - ρ_P) =…

… = 0,00015 m^3 (14000 - 10500)/(19300 - 10500) = 0,0000596 m^3

Poznać wagę złota, która zawiera koronę, którą mnożymy, dla gęstości złota:

Może ci służyć: zasada prawej ręki

MO = 19300 *0,00005966 = 11514 kg

Ponieważ masa korony wynosi 2,10 kg, wiemy, że Goldsmith skradzione 0,94858 kg.

Rozwiązane ćwiczenia

Ćwiczenie 1

Ogromny balon helowy jest w stanie utrzymać równowagę (bez wchodzenia lub schodzenia) do osoby.

Załóżmy, że waga osoby, a także kosz, struny i balon wynoszą 70 kg. Jaka jest objętość helu niezbędna do tego? Jaki rozmiar będzie miał balon?

Rozwiązanie

Zakładamy, że ciąg ten wytwarza głównie objętość helu i że ciąg pozostałych składników jest bardzo mały w porównaniu z helem, który zajmuje znacznie większą objętość.

W takim przypadku wymagana będzie objętość helu, zdolna do dostarczenia ciągu 70 kg +.

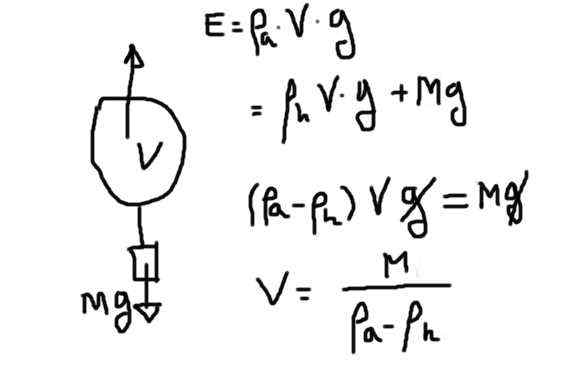Bezpłatny fdiaogram ciała pełen helu. Źródło: Przygotowane przez F. Zapata.

Pęd jest iloczyn objętości helu z powodu gęstości helu z powodu przyspieszenia grawitacji. Ten pęd musi zrekompensować ciężar helu plus wagę resztę.

Da⋅v⋅g = da⋅v⋅g + m⋅g

gdzie stwierdza się, że v = m / (da - dh)

V = 70 kg / (1.25 - 0,18) kg/m^3 = 65.4 m^3

To znaczy 65 jest wymaganych.4 m^3 helu pod ciśnieniem atmosferycznym w celu wsparcia.

Jeśli założymy sferyczny balon, możemy znaleźć promień tego samego z związku między objętością a promieniem kuli:

V = (4/3) ⋅π⋅r^3

Gdzie r = 2,49 m. Innymi słowy, wymagana będzie średnica 5 m pełna helu.

Ćwiczenie 2

Materiały o niższej gęstości, które woda unosi się w tym samym. Załóżmy, że masz kostki polistyrenowe (biały kork), drewno i lód. Jego gęstości w kg na metr sześcienny wynosi odpowiednio: 20, 450 i 915.

Znajdź, jaki ułamek całkowitej objętości jest poza wodą i jaka wysokość wyróżnia się w odniesieniu do powierzchni wody przyjmującej jako gęstość ostatnich 1000 kilogramów na metr sześcienny.

Rozwiązanie 

Wybór występuje, gdy masa ciała jest równa ciągu z powodu wody:

E = M⋅G

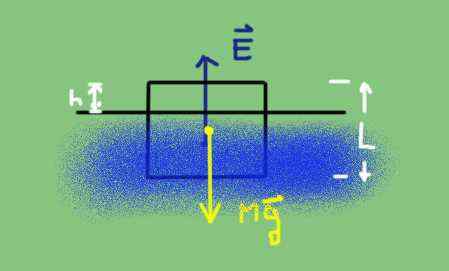Schemat wolnego ciała częściowo zanurzonego obiektu. Źródło: Przygotowane przez F. Zapata.

Waga to gęstość ciała DC pomnożona przez jego objętość V i przyspieszenie grawitacji g.

Pęd jest ciężarem przesuniętego płynu zgodnie z zasadą Archimedesa i jest obliczany przez pomnożenie gęstości d wody przez zanurzoną objętość V 'i przyspieszenie grawitacji.

To jest:

D⋅V'lg = DC⋅V⋅G

Co oznacza, że ​​zanurzona frakcja objętościowa jest równa ilorazu między gęstością ciała a gęstością wody.

(V '/v) = (dc/d) 

To znaczy, że wybitny ułamek wolumenu (v "/v) jest

(V "/v) = 1 - (dc/d)

Tak H Jest to wyjątkowa wysokość i L Strona kostki Ułamek objętościowy można zapisać jako

(H⋅l^2)/(l^3) = h/l, Innymi słowy, wybitny ułamek wysokości jest również

(h/l) = 1 - (dc/d)

Następnie wyniki żądanych materiałów to:

Polistyren (biały kork):

(H/l) = (v "/v) = 1 - (dc/d) = 1- (20/1000) = 98% z wody

Drewno:

(h/l) = (v "/v) = 1 - (dc/d) = 1- (450/1000) = 55% z wody

Lód:

(h/l) = (v "/v) = 1 - (dc/d) = 1- (915/1000) = 8.5% z wody

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill. 417-455.
2. Cengel Y, Cimbala J. 2011.Mechanika płynów. Podstawy i wnioski. Pierwsza edycja. McGraw Hill.
3. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 4. Płyny i termodynamika. Pod redakcją Douglas Figueroa (USB). 1 - 42.
4. Giles, r. 2010. Mechanika płynów i hydraulicznych. McGraw Hill. 
5. Rex, a. 2011. Podstawy fizyki. osoba. 239-263.
6. Tippens, s. 1. 2011. Fizyka: koncepcje i zastosowania. 7. edycja. McGraw Hill.