Wyjaśnienie stanu pierwszej równowagi, przykłady, ćwiczenia

First Bilans Warunek Wymaga to, aby wektor podsumowujący wszystkie siły działające na ciele był nieważny, tak że jest w spoczynku (równowaga statyczna) lub z jednolitym ruchem prostoliniowym (równowaga dynamiczna).

Ta suma sił jest niczym innym jak siłą netto, która działa na ciało, wyrażając ten tryb matematycznie:

F_Internet = 0

∑ F = 0

Rysunek 1. Budowniczowie starożytności zastosowali już pierwszy stan równowagi, o czym świadczy pomnik Stonehenge. Źródło: Pixabay.

W przestrzeni pierwszy warunek równowagi daje trzy równania, po jednym dla każdego wymiaru:

∑ f_X = 0; ∑ f_I = 0 i ∑ f_z = 0

Gdy równania te są spełnione, obiekt się nie porusza lub jeśli tak, będzie z stałą prędkością.

Obserwując wokół nas.

Dlatego stara się zrekompensować przyciąganie grawitacyjne Ziemi poprzez wsparcie, liny lub wsparcie, aby rzeczy pozostały na miejscu i nie poszły na ziemię.

Innym razem potrzebne jest zapobieganie zakłóceniu zewnętrznych pól elektromagnetycznych. W takim przypadku są to ładunki elektryczne, które muszą być w równowadze.

[TOC]

Przykłady

Duża liczba obiektów codziennych spełnia pierwszy stan równowagi, jest kwestią uważnej obserwacji:

Budynki

Budowniczowie szukają stabilności w konstrukcjach, aby użytkownicy zachowali bezpieczeństwo. Celem statycznym jest zbadanie warunków równowagi statycznej w budynkach, mostach, drogach i wszelkiego rodzaju strukturach.

Higafory i wiszące ostrzeżenia

Te urządzenia sygnalizacyjne muszą pozostać naprawione, aby spełnić swoje funkcje, dlatego podlegają kable, słupkom i pręciom w taki sposób, aby pierwszy warunek równowagi został spełniony.

Może ci służyć: trzecie prawo termodynamiki: wzory, równania, przykładyRysunek 2. Światła światła i wiszące ostrzeżenia są przedmiotem w taki sposób, że spełniają pierwszą warunek równowagi. Źródło: pxfuel.

Sterowniki równowagi elektrostudaszek

Gdy materiały przewodzące, takie jak miedź i inne metale, nabierają ładunku elektrycznego, wkrótce ustalono równowagę elektrostatyczną, pozostawiając nadwyżkę obciążenia na powierzchni przewodzącej. Wewnątrz pola elektrycznego wynosi zero.

Efekt ten jest często stosowany do izolowania urządzeń elektrycznych i elektronicznych pól zewnętrznych za pomocą SO -CALED FARADAY CAGE. Klatka jest wykonana z materiału przewodzącego i otacza sprzęt do ochrony.

Podczas burz samochody służą jako klatki Faraday, chroniąc mieszkańców przed porażeniami elektrycznymi.

Lampy sufitowe

W systemach oświetleniowych, takich jak wiszące lampy, pierwszy warunek równowagi służy do ustalenia ich na dachu, na podłodze lub ścianie.

Rysunek 3. Skomplikowana lampa dachowa zwana „pająki” spełnia pierwszy stan równowagi. Źródło: Pixabay.

Książki i obiekty na tabelach

Obiekty umieszczone na tabelach i półkach spełniają pierwszy warunek równowagi. Normalna siła, którą wsparcie wywiera na obiekty, jest odpowiedzialna za zrekompensowanie wagi.

Miara lepkości cieczy

Aby określić lepkość cieczy, sferyczny obiekt o znanej średnicy, która zobaczy jej prędkość z powodu oporu, zostanie zrzucona w środku. Prędkość kuli jest stała, jest w równowadze dynamicznej.

Większa lepkość cieczy, mniejsza prędkość, z jaką kula porusza się w środku.

Kroki w celu zastosowania pierwszego stanu równowagi

-Zrób schemat wolnego ciała, który pokazuje wszystkie siły, które działają na ciele (pomiń, co ciało wywiera na innych).

Może ci służyć: fizyka w średniowieczu

-Wybierz kartezjański układ współrzędnych, zapewniając, że jeśli to możliwe, siły znajdują się na dowolnej osie. Pozytywny adres jest zwykle przyjmowany w sensie ruchu lub możliwego ruchu.

-Określ elementy kartezjańskie każdej siły.

-Zastosuj drugie prawo Newtona dla każdego komponentu, jak ustalono na początku, istnieje system równań.

-Rozwiąż układ równań podniesionych w poprzednim kroku.

Rozwiązane ćwiczenia

- Ćwiczenie rozwiązane 1

Blok figury, masy M, Porusza się w dół na płaszczyźnie kąta θ ze stałą prędkością. Obliczyć wartość tarcia kinetycznego współczynnika μ_k, Jeśli masa bloku wynosi m = 5 kg i θ = 37º.

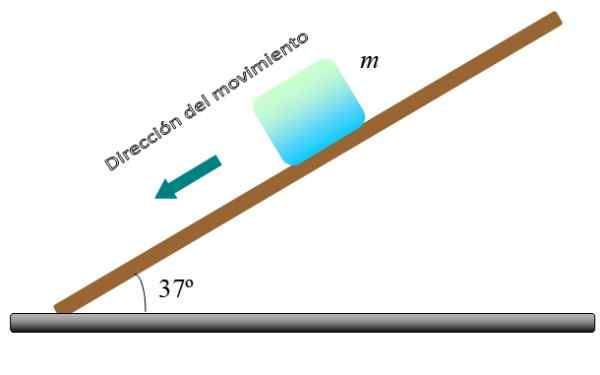Rysunek 4. Blok ślizga się ze stałą prędkością na pochylonej płaszczyźnie. Źródło: f. Zapata.

Rozwiązanie

Pierwszym krokiem jest narysowanie schematu wolnego ciała i wybór kartezjański układ współrzędnych, aby wyrazić każdy wektor siłowy. Siły działające na bloku to:

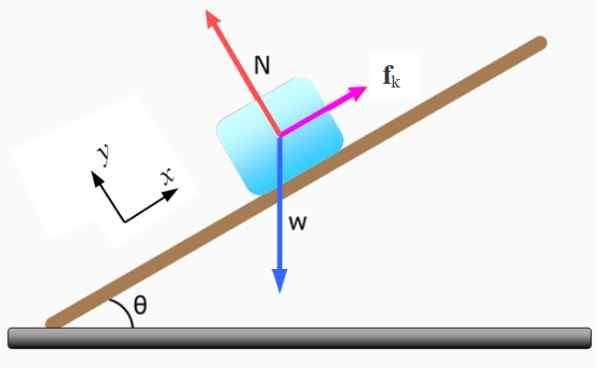Rysunek 5. Darmowy schemat ciała dla bloku. Źródło: f. Zapata.

-Normalny N wykonany przez pochyłą płaszczyznę, jest prostopadle do powierzchni tego.

-Waga W Jest skierowany pionowo.

-Tarcie kinetyczne F_k To sprzeciwia się ruchowi. Gdyby nie istniała, ciało zjechałoby z w dół z przyspieszeniem równym G.Senθ.

Jak waga W Jest pochylony w odniesieniu do wybranych osi współrzędnych, należy go podzielić na swoje komponenty kartezjańskie:

W_X = mg.Sen 37º = 5 kg x 9,8 m/s² x sin 37º = 29. 5 n
W_I = mg.COS 37º = 5 kg x 9,8 m/s² x cos 37º = 39.1 n

Drugie prawo Newtona jest teraz stosowane, dopasowując każdą sumę do 0, ponieważ bloku nie ma przyspieszenia podczas poruszania się ze stałą prędkością:

∑ f_I = N - w_I = 0
∑ f_X = W_X - F_k = 0

Wielkość tarcia kinetycznego jest proporcjonalna do wielkości normalnej, jest współczynnikiem tarcia kinetycznego μ_k Stała proporcjonalności.

Może ci służyć: presja bezwzględna: wzór, sposób obliczania, przykłady, ćwiczenia

F_k = μ_k N

W tym samym czasie:

N = w_I = 39.1 n

I również:

F_k = W_X

Dlatego:

29. 5 n = μ_k X 39.1 n

μ_k = 29. 5/39.1 = 0.75

- Ćwiczenie rozwiązane 2

Oblicz wielkość napięć, które obsługują masowy światło światła 33 kg, pokazane na rysunku:

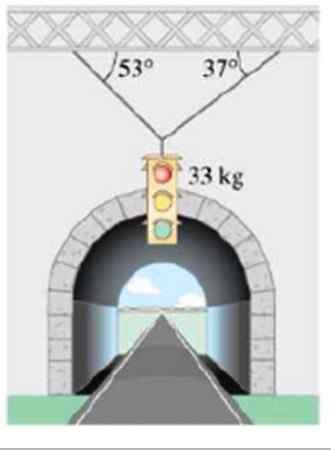Rysunek 6. Światło wisi za pomocą kabli. Źródło: Giancoli. Fizyka z aplikacjami.

Rozwiązanie

Schemat wolnego ciała odbywa się zarówno dla światła, jak i dla węzła, który trzyma kable:

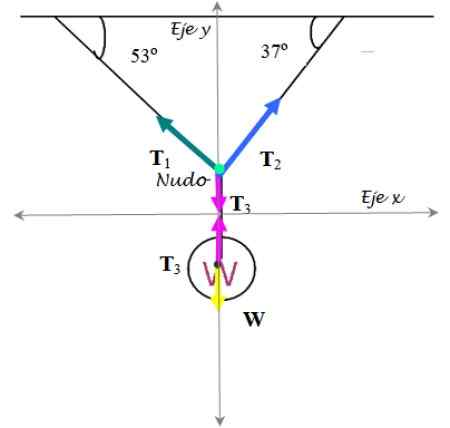Rysunek 7. Schemat wolnego ciała dla ćwiczeń rozwiązanych 2. Źródło: f. Zapata.

Sygnalizacja świetlna

O tym działaniu: napięcie t₃ W górę i waga w dół. Dlatego:

∑ f_I = W - t₃ = 0

Dlatego:

T₃ = 33 kg x 9.8 m/s² = 323.4 n

Węzeł

Napięcia rozkładają się w ich komponentach kartezjańskich:

∑ f_I = T₁ Sen 53º + T₂ Sen 37º - T₃ = 0
∑ f_X = T₂ Cos 37º - t₁ Cos 53º = 0

I uzyskuje się następujący układ równań liniowych z dwoma niewiadomymi₁  oraz T₂ :

- 0.6 t₁ + 0.8 t₂ = 0
0.8 t₁ + 0.6 t₂ = 323.4

Rozwiązaniem tego układu równań jest: t₁ = 258.7 n i t₂ = 194.0 n

Interesujące tematy

Warunki równowagi.

Drugi warunek równowagi.

Bibliografia

1. Bedford, 2000. DO. Mechanika inżynierii: statyczne. Addison Wesley.
2. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 4. Układy cząstek. Pod redakcją Douglas Figueroa (USB).
3. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1.
5. Wikipedia. Statyczny (mechaniczny). Odzyskane z: jest.Wikipedia.org.