Fale jednoznaczne wyrażenie matematyczne i przykłady

Fale jednoznaczne Są to te, które propagują się w jednym kierunku, niezależnie od tego, czy wibracja występuje, czy nie w tym samym kierunku propagacji. Dobrym ich przykładem jest fala, która porusza się wzdłuż napiętej liny jak gitara.

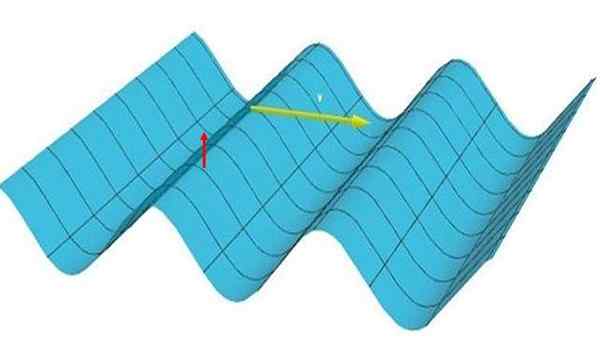
W płaskiej fali przechodzić, Cząstki wibrują pionowo (wspinają się i schodzą w dół, patrz czerwona strzałka na rycinie 1), ale jest to jedna -wymiar, ponieważ zakłócenia przemieszcza się w jednym kierunku, po żółtej strzałce.

Rysunek 1: Obraz reprezentuje fala o jeden wymiarowy. Zauważ, że grzbiety i doliny tworzą równoległe linie i prostopadle do kierunku propagacji. Źródło: Self Made.

Fale jednoznaczne pojawiają się dość często w życiu codziennym. W poniższej sekcji opisano kilka ich przykładów, a także fal, które nie są jednoznaczne, aby jasno ustalić różnice.

[TOC]

Przykłady fali jednowymiarowych i fal niewidzialnych

Fale jednoznaczne

Są to kilka przykładów jednej wymiarowej fal, które można łatwo zaobserwować:

- Puls dźwiękowy, który podróżuje przez prosty pasek, ponieważ jest to zakłócenie, które rozprzestrzenia się w całym pręcie.

- Fala, która przemieszcza kanał wodny, nawet gdy przemieszczenie powierzchni wody nie jest równoległe do kanału.

- Fale rozprzestrzeniające się na powierzchni lub przez trójwymiarową przestrzeń mogą być również jedno wymiarowe, pod warunkiem, że ich fronty falowe są samolotami równoległymi do siebie i podróżują w jednym kierunku.

Fale niewymiarowe

Przykład niewymiarowej fali znajduje się w falach, które powstają na powierzchni nieruchomej wody, gdy upuszczony jest kamień. Jest to dwuwymiarowa fala fali cylindrycznej.

Może ci służyć: dźwignia ramięRysunek 2. Obraz przedstawia przykład tego, co nie jest fala jednowymiarowa. Zauważ, że grzbiety i doliny tworzą koła, a kierunek propagacji jest promieniowy na zewnątrz, jest to dwuwymiarowa fala okrągła. Źródło: Pixabay.

Innym przykładem fali wymiarowej nieoświzyjnej jest fala dźwiękowa, która generuje petardę przez eksplozję na pewnej wysokości. To jest trzywymiarowa fala z sferycznymi frontami falowymi.

Matematyczna ekspresja jednej wymiarowej fali

Najbardziej ogólny sposób wyrażania jednej wymiarowej fali, która rozprzestrzenia się bez tłumienia w pozytywnym kierunku osi X i z prędkością v Jest matematycznie:

i (x, t) = f (x - v.T)

W tym wyrażeniu I reprezentuje zakłócenia w pozycji X Natychmiast T. Fali podaje się przez funkcję F. Na przykład funkcja fali pokazana na rycinie 1 to:  i (x, t) = cos (x - v t) a obraz fali odpowiada chwili t = 0.

Nazywana jest taka fala opisana przez funkcję cosinus lub zatok fala harmoniczna. Chociaż nie jest to jedyny przebieg, ma to ogromne znaczenie, ponieważ każda inna fala może być reprezentowana jako nakładanie się lub suma fal harmonicznych. To jest znajomy Twierdzenie Fouriera, Tak używane do opisania wszelkiego rodzaju sygnałów.

Kiedy fala porusza się w negatywnym kierunku osi x, po prostu się zmienia v przez -v W kłótni, bycie:

i (x, t) = g (x + v t)

Rycina 3 pokazuje animację fali, która przesuwa się w lewo: jest to forma zwana funkcją Lorentziana i jej Wyrażenie matematyczne to:

Może ci służyć: praca: formuła, jednostki, przykłady, ćwiczenia

i (x, t) = 1 / (1 + (x + 1⋅T)²

W tym przykładzie prędkość propagacji jest v = 1, -jednostka miejsca na każdą jednostkę czasu-.

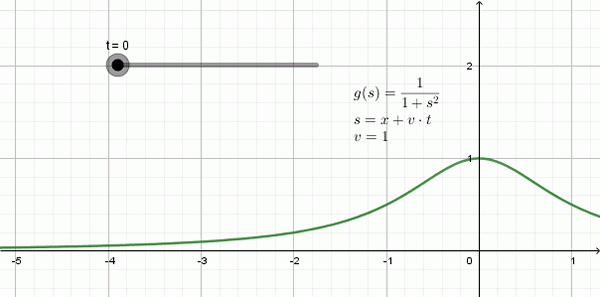Rysunek 3. Przykład fali Lorentzian, która szybko przemieszcza w lewo V = 1. Źródło: Przygotowane przez F. Zapata z Geogebra.

Równanie fali jednowymiarowe

Równanie fali jest równaniem w częściowych pochodnych, których rozwiązaniem jest oczywiście fala. Ustanawia matematyczny związek między częścią przestrzenną a jej częścią czasową i ma formę:

Rozwiązanie, które jest dokładnie funkcją y (x, t), można zweryfikować przez zastępowanie i rozwój w tym równaniu. Na przykład funkcje f (x - v t)  I  G (x + vt)  wspomniane, są to rozwiązania równań falowych.

Rozwiązany przykład

Następnie masz ogólne wyrażenie y (x, t) dla fali harmonicznej:

i (x, t) = a⋅CO (k⋅x ± Ω⋅t + θo)

a) Opisz fizyczne znaczenie parametrów A, k, ω I θo.

b) Jakie znaczenie mają znaki ± na argumencie Coseno?

c) Sprawdź, czy dane wyrażenie jest rzeczywiście rozwiązaniem równania falowego z poprzedniej sekcji i znajdź prędkość v propagacji.

Rozwiązanie)

Cechy fali znajdują się w następujących parametrach:

-DO reprezentuje amplituda lub „Wysokość fali”.

-K jest w Numer fali I jest to związane z długością fali λ Poprzez K = 2π/ λ.

-Ω To jest fekspansja kątowa I jest to związane z okres T Oscylacja fali przez

Ω = 2π/ t.

-θo To jest początkowa faza, który jest związany z punktem początkowym fali.

Może ci służyć: tarcie statyczne: współczynnik, przykład, ćwiczenie

Rozwiązanie B)

Znak ujemny jest pobierany, jeśli fala przemieszczy się w kierunku dodatnim osi x i znak dodatni w przeciwnym razie.

Rozwiązanie C)

Sprawdź, czy dane wyrażenie jest rozwiązaniem równania falowego jest proste: podejmowana jest częściowa pochodna funkcji i (x, t) Jeśli chodzi o x dwa razy, jest on częściowo pochodzący z T dwa razy, a następnie oba wyniki spełniają się, aby uzyskać równość:

Drugi pochodzący z X: ∂²i/ ∂x²= -K². DO⋅CO (k⋅x ± Ω⋅t + θo)

Drugi pochodzący z t: ∂²i/ ∂t²= -Ω². DO⋅CO (k⋅x ± Ω⋅t + θo)

Wyniki te są zastąpione w równaniu falowym:

 -k². DO⋅CO (k⋅x ± Ω⋅t + θo) = (1/v²) (-Ω². DO⋅CO (k⋅x ± Ω⋅t + θo))

Aż tak bardzo DO Ponieważ cosinus są uproszczone, ponieważ pojawiają się po obu stronach równości, a argument cosinus jest taki sam, dlatego wyrażenie jest zredukowane do:

-k² = (1/v²) (-Ω²)

Co pozwala uzyskać równanie v pod względem Ω I k:

v² = Ω² / k²

v = ± Ω / k

Bibliografia

1. E-edukacja. Równanie jednowymiarowych fal harmonicznych. Odzyskane z: e-diucative.Cathedu.Jest
2. Rincón fizyki. Zajęcia falowe. Źródło: fizyka.Blogspot.com.
3. Figueroa, zm. 2006. Fale i fizyka kwantowa. Seria: Fizyka nauk i inżynierii. Pod redakcją Douglas Figueroa. Uniwersytet Simon Bolivar. Caracas, Wenezuela.
4. Laboratorium fizyki. Ruch falowy. Odzyskany z: fisicalab.com.
5. Peirce, a. Wykład 21: Jedno wymiarowe równanie fali: Rozwiązanie D'Alemberta. Źródło: UBC.AC.
6. Równanie fali. Źródło: w:.Wikipedia.com