Formuły fal stacjonarnych, cechy, typy, przykłady

stojące fale Są to fale, które rozprzestrzeniły się w ograniczonej połowie, idąc w części przestrzeni, w przeciwieństwie do fali podróżujących, które podczas propagacji odchodzące od źródła, które je powstało i nie wraca do niego.

Są podstawą dźwięków wytwarzanych w instrumentach muzycznych, ponieważ powstają łatwo na stałych strunach, na jednym z końca. Są one również tworzone w napiętych błonach, takich jak bębny lub wewnętrzne rurki i konstrukcje, takie jak mosty i budynki.

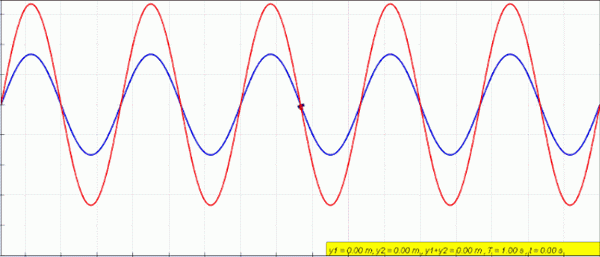Animacja stacjonarnej (czerwonej) fali stworzonej przez superpozycję lewego (niebieskiego) i prawej fali (zielony). Źródło: Lookangmany dzięki autorowi oryginalnej symulacji = Wolfgang Christian i Francisco Schembre Autor Easy Java Simulation = Francisco Schembre/CC BY-SA (https: // CreativeCommons.Org/licencje/nabrzeże/4.0)

Kiedy masz stałą linę na obu końcach, na przykład gitara, fale są tworzone z identyczną amplitudą i częstotliwością, które podróżują w przeciwnych zmysłach i łączą wytwarzanie zjawiska zwanego ingerencja.

Jeśli fale są w fazie, grzbiety i doliny są wyrównane i powodują falę o podwójnej amplitudzie. W takim przypadku mówi się o konstruktywnej ingerencji.

Ale jeśli fale, które zakłócają, nie są poza fazą, grzbiety jednego spełniają doliny innych, a amplituda wynosi zero. Jest to wówczas destrukcyjna ingerencja.

[TOC]

Wzory i równania

Głównymi elementami fali reprezentującej ją w przestrzeni i czasie są jego amplituda A, długość fali λ i częstotliwość kątowa ω.

Elementy fali. Źródło: Wikimedia Commons.

W reprezentacji matematycznej preferuje się używanie k, niż Numer fali o Liczba razy fala na jednostkę odbywa się. Dlatego jest to zdefiniowane przez długość fali λ, która jest odległością między dwiema dolinami lub dwoma grzbietami:

K = 2π/ λ

Podczas Częstotliwość kątowa Jest to związane z okresem lub czasem całkowitej oscylacji, na przykład:

Ω = 2π/ t

A także częstotliwość F jest podana przez:

F = ω / 2π

Dlatego:

F = 1/t

Ponadto fale poruszają się z prędkością v według:

v = λ.F

Matematyczne wyrażenie fali stacjonarnej

Matematycznie możemy wyrazić falę przez funkcję zatok lub funkcję cosinus. Załóżmy, że istnieją fale o równej amplitudzie A, długości fali λ i częstotliwości ω, rozprzestrzeniające się wzdłuż liny i w przeciwnych zmysłach:

I₁ = Sin (kx - ωt)

I₂ = Sin (kx + ωt)

Dodając je, znajdujemy wynikową falę i_R:

I_R = y₁ + I₂ = Sen (kx - ωt) + sin (kx + ωt)

Istnieje tożsamość trygonometryczna, aby znaleźć sumę:

Może ci służyć: co to jest względne i absolutne szorstkość?

sin α + sin β = 2 sin (α + β)/2 . cos (α - β)/2

Poprzez tę tożsamość, wynikowa fala i_R zostaje:

I_R = [2a Sen KX] . cos ωt

Lokalizacja węzłów i brzucha

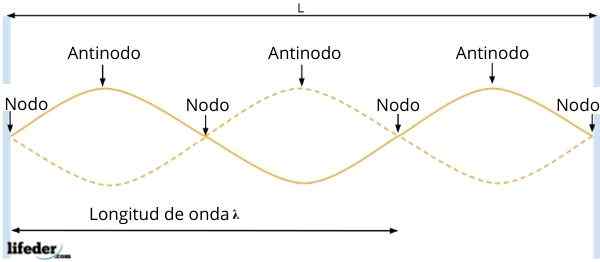Antinodos lub brzuchy i węzły

Powstała fala ma amplitudę do_R = 2ase Kx, co zależy od położenia cząstki. Następnie, w punktach, dla których sen kx = 0, amplituda fali jest anulowana, to znaczy nie ma wibracji.

Te punkty to:

Kx = π, 2π, 3π ..

Jako k = 2 π/ λ:

(2 π/ λ) x = π, 2π, 3π ..

x = λ/2, λ, 3λ/2 ..

W takich punktach występuje niszczycielska zakłócenia i są one nazywane węzły. Są one oddzielone odległością równą λ/2, jak wydedukowano z poprzedniego wyniku.

A między dwoma kolejnymi węzłami są Antinodos lub brzuch, w którym amplituda fali jest maksymalna, ponieważ występuje konstruktywna interferencja. Występują, kiedy:

sin kx = ± 1

Kx = ± π/2, 3π/2, 5π/2 ..

Ponownie k = 2 π/ λ, a następnie:

x = λ /4, 3λ /4, 5λ /4, ..

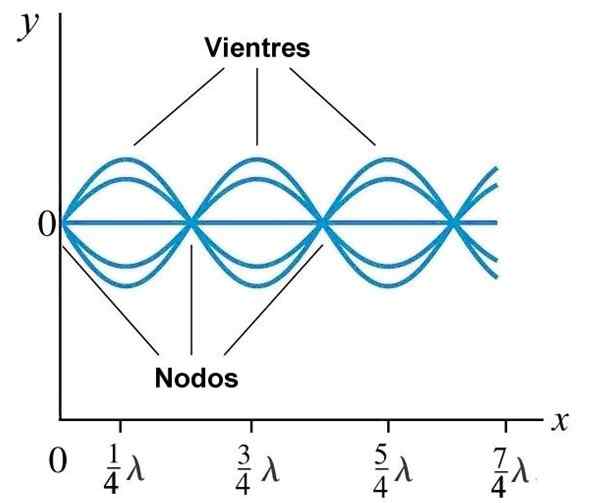Brzuch lub antynody i węzły w fali stacjonarnej wygenerowanej na linie o stałym końcu przy x = 0. Źródło: Wikimedia Commons.

Normalne tryby na linie

Warunki graniczne na linie określają, jak są długości fali i częstotliwości. Jeśli lina o długości l jest naprawiona przez dwa końce, nie może wibrować żadnej częstotliwości, ponieważ punkty, w których lina jest ustalona, ​​to już węzły.

Ponadto rozdział między sąsiednimi węzłami wynosi λ/2, a między węzłem a brzuchem wynosi λ/4, w ten sposób tylko dla niektórych długości fali są wytwarzane stacjonarne: te, w których liczba całkowita n z λ/2 wewnątrz jest dostosowana z ::

(λ/2) = L, z n = 1, 2, 3, 4 .. .

Dlatego:

λ = 2l/n

Harmoniczne

Różne wartości pobrane λ są wywoływane harmonia. Tak więc mamy:

-Pierwsza harmoniczna: λ = 2L

-Druga harmoniczna: λ = L

-Trzecia harmoniczna: λ = 2 l/3

-Pokój harmoniczny: λ = l/2

I tak dalej.

Prędkość i częstotliwość

Chociaż fala stacjonarna wydaje się nie poruszać, równanie jest nadal ważne:

v = λ. F

Dlatego:

v = (2L/N) . F

F = nv/2l

Teraz można wykazać, że prędkość, z jaką fala porusza się w linie, zależy od napięcia t w tym samym i jego gęstości liniowej masy μ (masa na jednostkę długości) jako:

Dlatego:

Może ci służyć: obciążenia martwe: charakterystyka, obliczenia, przykłady

Cechy fali stacjonarnych

-Gdy fale są stacjonarne, powstała fala nie rozprzestrzenia się jak jej komponenty, które przechodzą z jednego miejsca do drugiego. Są punkty, w których y = 0, ponieważ nie ma wibracji: węzły, innymi słowy, amplituda do_R Jest zero.

-Matematyczna ekspresja fali stacjonarnej składa się z iloczyn części przestrzennej (która zależy od współrzędnych X lub współrzędnych przestrzeni) i części czasowej.

-Wśród węzłów powstałe czarna fala oscyluje w jednym miejscu, podczas gdy fale, które przechodzą z jednego miejsca do drugiego, są tam przestarzałe.

-Tylko w węzłach energia nie jest transportowana, ponieważ jest to proporcjonalne do kwadratu amplitudy, ale jest uwięzione między węzłami.

-Odległość między sąsiednimi węzłami wynosi połowa długości fali.

-Punkty, w których ustalona jest lina, są również uważane za węzły.

Chłopaki

Fale stacjonarne w wymiarze

Fale w ustalonej linie są przykładami fal stacjonarnych w wymiarze, których opisy matematyczne zaproponowaliśmy w poprzednich sekcjach.

Fale stacjonarne w dwóch i trzech wymiarach

Fale stacjonarne można również przedstawić w dwóch i trzech wymiarach, będąc nieco bardziej złożonym opisem matematycznym.

Przykłady wyścigów Ondas

Ustalone struny

-String ustalony przez ekstremalne oscylowane ręcznie lub jednym tłokiem przez drugi generuje fale stacjonarne na jego długości.

Instrumenty muzyczne

Fale stacjonarne są tworzone w instrumentach muzycznych, takich jak wiolonczel. Źródło: Pixabay.

-Podczas gry na instrumentach smyczkowych, takich jak gitara, harfa, skrzypce i fortepian.

W lampach powietrznych tworzone są również fale stloverowe, takie jak rurki narządów.

Budynki i mosty

Fale stacjonarne powstają w strukturach takich jak mosty i budynki. Niezwykłym przypadkiem był most wiszący Tacoma w pobliżu miasta Seattle, Stany Zjednoczone. Krótko po zainaugurowaniu w 1940 r. Most ten zawalił.

Częstotliwość wiatru dopasowana do częstotliwości naturalnej mostu, tworząc w tym fale stacjonarne, które rosły ich amplitudy, dopóki most się nie zawala. Zjawisko jest znane jako rezonans.

Może ci służyć: odbicie światła

Seiches

W portach jest bardzo ciekawy zjawisko Seiche, w którym fale morza wytwarzają duże oscylacje. Jest tak, ponieważ wody w porcie są dość zamknięte, chociaż wody oceaniczne wnikają co jakiś czas przez wejście do portu.

Wody portowe poruszają się z własną częstotliwością, a także w oceanie. Jeśli oba wody pasują do ich częstotliwości, istnieje duża fala stacjonarna z powodu rezonansu, jak to się stało z mostem Tacoma.

Seiches Mogą również występować w jeziorach, zbiornikach, basenach i innych zbiornikach wodnych ograniczonych przez powierzchnie.

Zbiorniki

Fale stacjonarne mogą być tworzone w fishbowl transportowanej przez osobę, jeśli częstotliwość, z którą osoba jest równa częstotliwości huśtawki wody.

Ćwiczenie rozwiązane

Lina gitarowa ma l = 0.9 m i gęstość ciasta liniowego μ = 0.005 kg/m. Jest poddawany 72 n napięcia, a jego tryb wibracji jest tym, który pokazuje figurę, z amplitudą 2a = 0.5 cm.

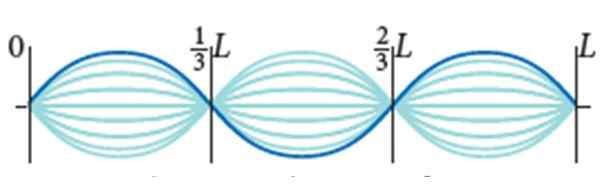Fale stacjonarne na gitarowej linie. Źródło: Bauer, w. Fizyczny.

Znajdować:

a) Prędkość propagacji

b) Częstotliwość fali

c) Odpowiednie równanie fali stacjonarnej.

Rozwiązanie

Poprzez:

Jest uzyskiwany;

V = [72 N/(0.005 kg/m)]^1/2  = 120 m/s.

Rozwiązanie b

Odległość między dwoma sąsiednimi węzłami wynosi λ/2, dlatego:

(2/3) L - (1/3) L = λ/2

(1/3) L = λ/2

λ = 2L/3 = 2 x 0.90 m / 3 = 0.60 m.

Jak v = λ.F

F = (120 m/ s)/ 0.60 m = 200 s^-1= 200 Hz.

Rozwiązanie c

Równanie to:

I_R = [2a Sen KX] . cos ωt

Musimy zastąpić wartości:

K = 2π/ λ = k = 2π/ 0.60 m = 10 π/3

F = ω / 2π

Ω = 2π x 200 Hz = 400 π Hz.

Amplituda 2A jest już podana przez stwierdzenie:

2a = 0.5 cm = 5 x 10 ^-3 M.

Dlatego:

I_R = 5 x 10 ^-3 M . sin [(10π/3) x] . cos (400πt) =

= 0.5 cm . sin [(10π/3) x] . cos (400πt)

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
2. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 7. Fale i fizyka kwantowa. Pod redakcją Douglas Figueroa (USB).
3. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
4. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wyd. Cengage Learning.
5. Tipler, str. (2006) Physics for Science and Technology. Ed. Tom 1. Redakcja Reverted.
6. Wikipedia. Seiche. Odzyskane z: jest.Wikipedia.org.