Cechy fali Senoidalnej, części, obliczenia, przykłady

Fale sinusoidalne Są to wzorce fali, które można matematycznie opisywać przez funkcje sinus i cosinus. Słusznie opisują naturalne zdarzenia i zmienne znaki w czasie, takie jak napięcia wytwarzane przez rośliny elektryczne, a następnie wykorzystywane w domach, branżach i ulicach.

Elementy elektryczne, takie jak rezystancje, kondensatory i indukcyjności, które łączą się z sinusoidalnymi wejściami napięcia, również dają odpowiedzi również sinusoidalne. Matematyka zastosowana w ich opisie jest stosunkowo prosta i została dokładnie zbadana.

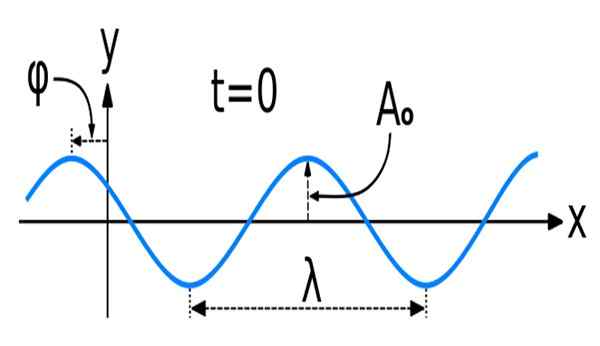
Rysunek 1. Fala sinusoidalna o niektórych głównych cechach przestrzennych: amplituda, długość fali i faza. Źródło: Wikimedia Commons. WAVE_NEW_SINE.SVG: KraaaLenestoriginally stworzony jako fala cosinus, przez użytkownika: Pelegs, jako plik: fave_new.Prace SVGDERIVATIALNE: DAVE3457 [CC BY-SA 3.0 (https: // creativeCommons.Org/licencje/by-sa/3.0)]

Matematyka fal sinusoidalnych lub sinusoidalnych, jak są również znane, to materia z funkcji sinus i cosinus.

Są to powtarzające się funkcje, co oznacza okresowość. Oba mają ten sam sposób, z zastrzeżeniem, że cosinus jest wysiedlony w lewo w odniesieniu do piersi w pokoju rowerowym. Obserwuje się na rycinie 2:

Rysunek 2. Funkcje SEN X i COS X są wyparte w odniesieniu do drugiego. Źródło: f. Zapata.

Następnie cos x = sin (x + π/2). Za pomocą tych funkcji reprezentuje się fala sinusoidalna. Aby to zrobić, dana wielkość jest umieszczana na osi pionowej, podczas gdy w osi poziomej czasu jest umieszczony.

Powtarzająca się jakość tych funkcji jest również doceniana na powyższym wykresie: wzór powtarza się w sposób ciągły i regularnie. Dzięki tym funkcjom możesz wyrażać napięcia i prądy typu sinianskiego zmieniające się w czasie, umieszczając na osi pionowej zamiast na I, A v lub jeden Siema reprezentować napięcie lub prąd oraz na osi poziomej zamiast na X, T pogoda.

Najbardziej ogólnym sposobem wyrażania fali sinusoidalnej jest:

v (t) = v_M Sin (ωt+φ)

Następnie pogłębimy znaczenie tego wyrażenia, definiując niektóre podstawowe terminy w celu scharakteryzowania fali sinusoidalnej.

[TOC]

Imprezy

Okres, amplituda, częstotliwość, cykl i faza to pojęcia dotyczą fali okresowych lub powtarzalnych i są ważne, aby je właściwie scharakteryzować.

Okres

Funkcja okresowa, taka jak wspomniane, która jest powtarzana w regularnych odstępach czasu, zawsze spełnia następującą właściwość:

f (t) = f (t + t) = f (t + 2t) = f (t + 3t) =… .

Gdzie T Jest to kwota o nazwie fala, I jest to czas, aby powtórzyć fazę tego samego. W międzynarodowych jednostkach systemowych okres jest mierzony w ciągu kilku sekund.

Amplituda

Zgodnie z ogólnym wyrazem fali Senoidalnej v (t) = v_M sin (ωt+φ), v_M Jest to maksymalna wartość funkcji, która występuje, kiedy sin (ωt+φ) = 1 (Pamiętając, że największą wartością, jaką przyznaje zatokę i funkcja cosinusa, jest 1). Ta maksymalna wartość jest dokładnie Amplituda fal, znany również jako amplituda szczytowa.

W przypadku napięcia będzie mierzone w woltach, a jeśli jest to prąd, który będzie w wzmacniaczach. W fali sinusoidalnej szerokość jest stała, ale w innych typach fali amplituda może się różnić.

Może ci służyć: termometr oporności: charakterystyka, operacja, użycia

Cykl

Jest częścią fali zawartej w okresie. Na poprzedniej figurze okres został wykonany przez pomiar go z dwóch kolejnych pików lub grzbietów, ale można go zacząć mierzyć z innych części fali, podczas gdy są one ograniczone okresem.

Uwaga na poniższym rysunku, ponieważ jeden cykl obejmuje od jednego punktu do drugiego z tą samą wartością (wysokością) i tym samym nachyleniem (nachylenie).

Rysunek 3. W fali sinusoidalnej cykl zawsze odbywa się przez okres. Ważne jest to, że punkt początkowy i koniec znajdują się na tej samej wysokości. Źródło: Boylestad. Wprowadzenie do analizy obwodów. osoba.

Częstotliwość

Jest to ilość cykli, które występują w 1 sekundzie i są powiązane z argumentem funkcji zatok: ωt. Częstotliwość jest oznaczona jako F I jest mierzony w cyklach na sekundę lub Hertz (HZ) w systemie międzynarodowym.

Częstotliwość jest odwrotną ilością okresu, dlatego:

F = 1/t

Podczas częstotliwości F jest związane z Częstotliwość kątowa ω (pulsacja) jako:

Ω = 2πF

Częstotliwość kątowa jest wyrażana w radianach /drugie w systemie międzynarodowym, ale radianie są bezwymiarowe, a zatem częstotliwość F i częstotliwość kątowa Ω Mają te same wymiary. Zauważ, że produkt ωt w rezultacie daje radianom i należy je wziąć pod uwagę przy użyciu kalkulatora w celu uzyskania wartości Sen ωt.

Faza

Odpowiada poziomemu przemieszczeniu doświadczonemu przez falę, w odniesieniu do czasu traktowanego jako odniesienie.

Na poniższym rysunku zielona fala jest w odniesieniu do czerwieni T_D. W są dwie fale sinusoidalne faza Gdy częstotliwość i faza są takie same. Jeśli faza różni się, to są w luka. Rysunek 2 fale są również przestarzałe.

Rysunek 4. Fale sinusidalne. Źródło: Wikimedia Commons. Nie dostarczył autora, który można odczytać w maszynie. Kanjo ~ Commonswiki przyjęty (na podstawie roszczeń dotyczących praw autorskich). [Domena publiczna].

Jeśli częstotliwość fal jest inna, będą one w fazie, gdy faza ωt+φ Bądź taki sam w obu falach w niektórych momentach.

Generator fali Senoidalnej

Istnieje wiele sposobów uzyskania sygnału w kształcie sinusoidalnego. Domowe biegi zapewniają im.

Zastosowanie prawa Faradaya

Dość prosty sposób na uzyskanie sygnału sinusoidalnego jest użycie prawa Faradaya. Wskazuje to, że w zamkniętym obwodzie prądu, na przykład pętli, umieszczonej na środku pola magnetycznego, indukowany prąd jest generowany, gdy przepływ pola magnetycznego przez niego zmienia się w czasie. W związku z tym Indukowane napięcie albo indukowane fem.

Przepływ pola magnetycznego zmienia się, jeśli pętla jest obracana ze stałą szybkością kątową pośrodku pola utworzonego między biegunami N i S magnetu pokazanego na rysunku.

Może ci służyć: Neptune (planeta)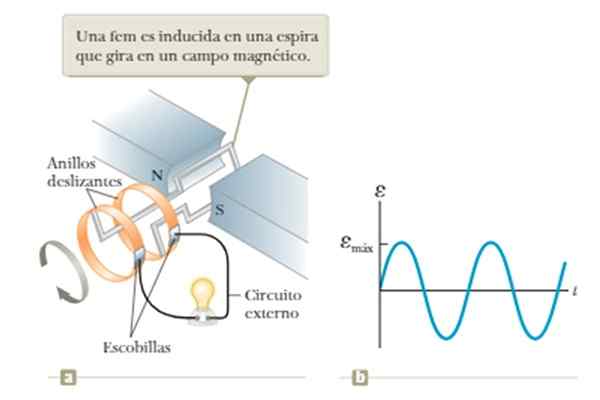Rysunek 5. Generator fal oparty na prawie indukcyjnym Faradaya. Źródło: Źródło: Raymond A. Serway, Jonh W. Jewett [CC BY-SA 4.0 (https: // creativeCommons.Org/licencje/nabrzeże/4.0)].

Ograniczeniem tego operacyjnego jest zależność od napięcia uzyskanego z częstotliwością obrotu pętli, co będzie widać bardziej szczegółowo w przykładzie 1 sekcji przykładów później.

Oscylator Wien

Inny sposób na uzyskanie fali sinusoidalnej, tym razem z elektronem. W ten sposób uzyskuje się fale sinusoidalne, których częstotliwość i amplituda użytkownik może modyfikować zgodnie z wygodą, poprzez regulację przełącznika.

Rysunek pokazuje generator sygnału sinusoidalnego, z którym można również uzyskać inne przebiegi: między innymi trójkątne i kwadraty.

Rysunek 6. Generator sygnału. Źródło: Źródło: Wikimedia Commons. Optregat at English Wikipedia [CC BY-SA 3.0 (https: // creativeCommons.Org/licencje/by-sa/3.0)].

Jak obliczyć fale sinusoidalne?

Aby wykonać obliczenia obejmujące fale sinusoidalne, stosuje się kalkulator naukowy, który ma funkcje trygonometryczne zatok i cosinus, a także odwrotnie. Te kalkulatory mają tryby do pracy pod kątem w stopniach lub radiach, i łatwo jest przekonwertować jeden sposób na drugi. Współczynnik konwersji to:

180 ° = π Radian.

Zgodnie z modelem kalkulatora należy nawigować za pomocą klucza trybu, aby znaleźć opcję stopnia, która pozwala pracować nad funkcjami trygonometrycznymi w stopniach lub opcji RAD, aby bezpośrednio pracować.

Na przykład sin 25 º = 0.4226 z kalkulatorem umieszczonym w trybie DEG. Przekształcając 25 ° w promienia, dostajesz 0.4363 Radiany i Sen 0.4363 rad = 0.425889 ≈ 0.4226.

Oscyloskop

Oscyloskop to aparat, który pozwala wizualizować na ekranie znaków napięć i prądów zarówno na przemian, jak i bezpośredni. Ma pokrętła, aby dostosować rozmiar sygnału na siatce, jak pokazano na poniższym rysunku:

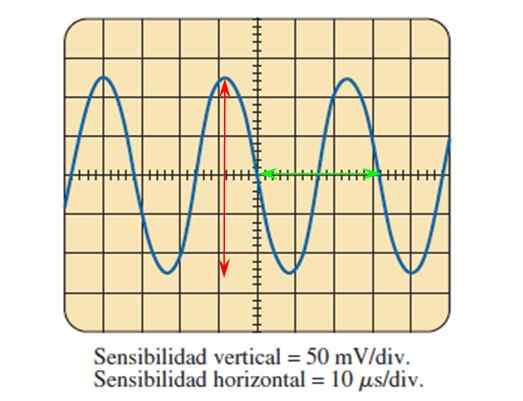Rysunek 7. Sygnał sinusoidalny zmierzony za pomocą oscyloskopu. Źródło: Boylestad.

Przez obraz dostarczony przez oscyloskop i znajomość regulacji czułości w obu osiach, możliwe jest obliczenie parametrów fali opisanych powyżej.

Może ci służyć: galaktyki eliptyczne: tworzenie, cechy, typy, przykłady

Rysunek pokazuje sygnał napięcia sinusoidalnego jako funkcję czasu, w którym każdy podział osi pionowej jest wart 50 miliWoltów, podczas gdy w osi poziomej każda dywizja jest warta 10 mikrosekund.

Amplituda szczytowa do szczytu liczy podziały, które fala obejmuje pionowo, pomagając w czerwonej strzałce:

5 podziałów jest liczone za pomocą czerwonej strzałki, więc napięcie szczytowe Pico to:

V_pp = 5 podziałów x 50 mV/podział = 250 mV.

Napięcie pico V_P Jest mierzony ze osi poziomej, wynoszącym 125 mV.

Aby znaleźć okres, mierzony cykl, na przykład ten wyznaczony przez zieloną strzałkę, która obejmuje 3.2 podziały, wówczas okres to:

T = 3.2 podziały x 10 mikrosekund/podział = 32 mikrosekund = 32 μs

Przykłady

Przykład 1

W przypadku generatora na rycinie 3 wykazaj z prawa Faradaya, że ​​napięcie indukowane ma sinus. Załóżmy, że pętla składa się z n zakrętów zamiast jednego, wszystkie z tym samym obszarem A i obracają się ze stałą szybkością kątową ω na środku pola magnetycznego B mundur.

Rozwiązanie

Prawo Faradaya mówi, że indukowana FEM ε Jest:

ε = -n (dφ_B /dt)

Gdzie Φ_B Jest to przepływ pola magnetycznego, który będzie zmienny, ponieważ zależy od tego, jak pętla jest narażona na pole w każdej chwili. Znak ujemny po prostu opisuje fakt, że ten FES sprzeciwia się przyczynie, która go wytwarza (prawo Lenza). Przepływ z powodu pojedynczej pętli to:

Φ_B = B.DO.cos θ

θ jest kątem, w którym formuje się normalny wektor do płaszczyzny pętli B Gdy obrót ma miejsce (patrz rysunek), kąt ten naturalnie zmienia się jako:

θ = ωt

Aby: Φ_B = B.DO.cos θ = b.DO.sałata ωt. Teraz musisz po prostu wyprowadzić to wyrażenie w odniesieniu do czasu, a wraz z nim uzyskuje się indukowane MES:

ε = -n.d (b.DO.sałata ωt) /dt

Jak pole B Jest jednolity, a obszar spaza się nie różni, opuszczają pochodną:

ε = -nba. D (cos ωt) /dt = ωnba. Sen ωt

Przykład 2

Pętla ma obszar 0.100 m² i przejdź do 60.0 rev/s, z osi obrotu prostopadłego do jednolitego pola magnetycznego 0.200 t. Wiedząc, że cewka ma 1000 zakrętów, aby znaleźć: a) maksymalne wygenerowane MES, b) Orientacja cewki w stosunku do pola magnetycznego, gdy występuje maksymalna indukowana MES.

Cyfra 8. Spirala n okrążeń rozbity na środku jednolitego pola magnetycznego i generuje sygnał sinusoidalny. Źródło: r. Serwera, fizyka nauk i inżynierii. Głośność 2. Cengage Learning.

Rozwiązanie

a) Maksymalna to MES ε_Max = Ωnba

Przed przystąpieniem do wymiany wartości należy przekazać częstotliwość 60 obrotów na jednostki systemu międzynarodowego. Wiadomo, że 1 rewolucja jest równoważna radanom lub 2p:

60.0 Rev/s = 120p Radiany/s

ε_Max = Radian 120p x 1000 okrążeń x 0.200 t x 0.100 m² = 7539.82 V = 7.5 kV

b) Gdy nastąpi ta wartość Sen ωt = 1 W związku z tym:

ωt = θ = 90º,

W tym przypadku płaszczyzna spiralna jest równoległa B, tak, że normalny wektor do wspomnianego płaszczyzny tworzy 90º z polem. Dzieje się tak, gdy czarny wektor na rycinie 8 jest prostopadły do ​​zielonego wektora reprezentującego pole magnetyczne.

Bibliografia

1. Boylestad, r. 2011. Wprowadzenie do analizy obwodów. 12. Wydanie. osoba. 327-376.
2. Figueroa, zm. 2005. Elektromagnetyzm. Seria fizyczna dla nauki i inżynierii. Tom 6. Edytowane przez d. Figueroa. Uniwersytet Simon Bolivar. 115 i 244-245.
3. Figueroa, zm. 2006. Laboratorium fizyki 2. Redakcja równowagi. 03-1 i 14-1.
4. Fale sinusoidalne. Wyjazd z: Iessierradegara.com
5. Serway, r. 2008.Fizyka nauk i inżynierii. Głośność 2. Cengage Learning. 881-884