Notacja opracowała to, co jest, przykłady i ćwiczenia
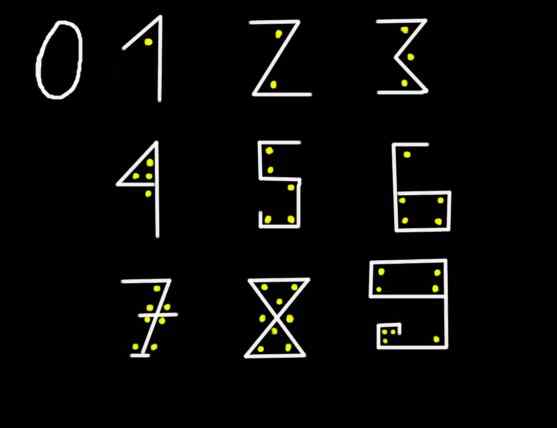
- 1249
- 256
- Eliasz Dubiel
rozwinięta notacja Jest to taki, w którym liczba numeryczna jest wyrażona jako suma, w której wartość pozycyjna każdej cyfry, która tworzy liczbę.
Na przykład podczas pisania postaci takiej jak 2345 każda cyfra ma hierarchię pozycyjną. Czytanie właściwej ekstremalnej cyfry po lewej stronie hierarchia lub wartość rośnie.
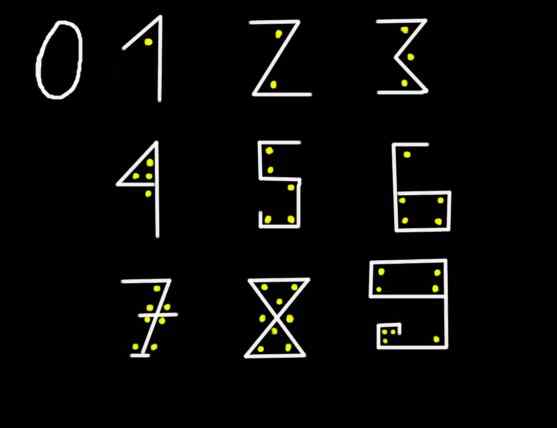 Rysunek 1. Z dziewięcioma grafemami można przedstawić dowolną liczbę.
Rysunek 1. Z dziewięcioma grafemami można przedstawić dowolną liczbę. Na rycinie 2345 cyfra 5 reprezentuje pięć jednostek, cyfra 4 reprezentuje cztery dziesiątki, 3 odpowiada trzeciej pozycji od lewej do prawej, a zatem 3 reprezentuje trzystu setek, w końcu 2 reprezentuje dwa tysiące. Oznacza to, że w rozwiniętej lub rozszerzonej notacji rysunek 2345 jest napisany w ten sposób:
2345 = 2 tysiące + 3set + 4 dziesiątki + 5 jednostek
Ale można go również wyrazić w następujący sposób:
2345 = 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1.
Rysunek 2345 może być również napisany jako suma mocy 10:
2345 = 2 x 10^3 + 3 x 10^2 + 4 x 10^1 + 5 x 10^0
Gdzie circlejo ^ oznacza podniesienie wskazanego wykładnika. Na przykład 10^3 = 10 x 10 x 10 = 1000. Innym sposobem pisania wykładników jest nadzór:
2345 = 2 x 103 + 3 x 102 + 4 x 101 + 5 x 100
[TOC]
System numerowania pozycji
System liczb arabskich to liczby używane codziennie w zdecydowanej większości kontynentów i krajów na świecie. Liczby arabskie są systemem bazowym 10, ponieważ do pisania dowolnej liczby używanych jest dziesięć symboli lub grafemów. Te dziesięć symboli to:
0 1 2 3 4 5 6 7 8 9
Z tylko jednym z tych symboli można wyrazić liczby od zera do dziewięciu. Aby wyrazić liczby większe niż dziewięć, układ pozycyjny oparty na dziesięciu. Rysunek 10 to tuzin i zero jednostek. Rysunek 11 to tuzin i jednostka. Rycina 123 (sto dwadzieścia trzy) to sto, dwa dziesiątki i trzy jednostki. Napisane w formie mocy dziesięciu numer 123 będzie:
Może ci służyć: 60 dzielników1 × 10^2 + 2 × 10^1 + 3 × 10^0
Gdzie:
10^2 = 10 x 10 = 100
10^1 = 10
10^0 = 1.
Z tym przykładem jasne jest, że położenie cyfry na końcu jest położenie 0 i reprezentuje liczbę jednostek, położenie drugiej cyfry od prawej do lewej to pozycja 1 i reprezentuje liczbę dziesiątek, trzecią cyfrę (po prawej stronie do prawej do po lewej) ma pozycję 2 i reprezentuje setki.
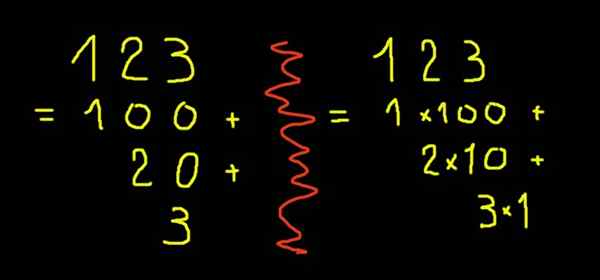 Rysunek 2. Rozwinięte notację z ryc. 123.
Rysunek 2. Rozwinięte notację z ryc. 123. Liczby ułamkowe lub dziesiętne
Z dziesiętnym systemem pozycji jest to również możliwe.
Aby reprezentować ułamek ½ w arabskim systemie dziesiętnym, to znaczy połowa jednostki jest napisana:
½ = 0,5
Aby osiągnąć to wyrażenie w naszym systemie na podstawie 10, dokonano następujących operacji:
1- Mnoż licznik i mianownik dla 5, aby mieć równoważną frakcję 5/10 = 1/2.
2- Podziel przez 10 jest równoważny z mnożeniem przez moc opartą na dziesięciu z wykładnikiem mniejszym (10^-1), czyli 5/10 = 5 × 10^-1.
3- Wykładnik ujemny wskazuje, ile razy cyfra wskazana z położenia urządzenia jest uruchamiana lub ustawiona, w naszym przypadku wynosiłaby 0,5.
4- ½ = 0,5 w rozszerzonej notacji Jest napisane w ten sposób:
0,5 = 0x10^0 + 5 × 10^-1
Gdzie 10^-1 = 0,1 to dziesiąta (ułamek odpowiadający jednostce podzielonej na 10 równych części).
W ten sposób liczba 0,5 odpowiada pięciu dziesiątym, ale liczba 0,05 odpowiada 5 setnym i 0,005 do 5 tysięcy.
Może ci służyć: dlaczego algebra jest ważna w niektórych codziennych sytuacjach?Opracowane przykłady notacji
Przykład 1
Biorąc pod uwagę figurę 40201 w notacji standardowej, przekonwertuj ją na rozwiniętą notację.
Rozwiązanie:
4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1 = 40201
Przykład 2
Napisz frakcję ¾ w rozszerzonej notacji.
Rozwiązanie:
W takim przypadku są trzy czwarte jednostki.
3/4 = 15/20 = 75/100 = 0,75 = 7/10 + 5/100 =
7 × 10^-1 + 5 × 10^-2.
Powiedział w słowach, gdyby tak:
Frakcja ¾ odpowiada siedmiu dziesiątom plus pięć setnych.
Rozwinięte ćwiczenia notacyjne
Ćwiczenie 1
Powiedz słowami wyrażenie opracowane z figury 40201 przykładu 1.
Rozwiązanie:
Rozwinięta notacja jest taka:
40201 = 4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1
Że w języku słów mówi się:
Cztery dziesiątki tysięcy plus tysiące, plus dwieście, więcej zero dziesiątek plus jednostka.
Ćwiczenie 2
Wyrażaj słowa poprzednia figura i rozbij odpowiadającą opracowaną frazę.
Rozwiązanie:
Figura 40201 słowami jest wyrażona w następujący sposób:
Czterdzieści tysięcy dwieście jeden
Poprzednia fraza może rozwinąć się jako:
40 × 1000 + 2 × 100 + 1
Można powiedzieć, że sposób wymówienia liczb jest opracowany na wpół sposób wyrażania tego.
Ćwiczenie 3
Napisz numer 7/3 opracowany.
Rozwiązanie:
Jest to liczba wyrażona jako niewłaściwa ułamek, ponieważ ponieważ licznik jest większy niż mianownik, liczba jest większa niż jednostka.
Ta niewłaściwa ułamek można rozbić jako sumę frakcji 6/3 + 1/3. Pierwsza z frakcji powoduje całkowitą liczbę 2, podczas gdy 1/3 = 0,333333, gdzie cyfra 3 jest powtarzana w nieskończoność. Tak, że ekspresja dziesiętna rozwinięta z figury 7/3 zawsze będzie przybliżonym wyrażeniem:
Może ci służyć: czworobok: elementy, właściwości, klasyfikacja, przykłady7/3 = 2 + 1/3 ≃ 2 + 0,333 = 2 + 3 × 10^-1 + 3 × 10^-2 + 3 × 10^-3.
Ćwiczenie 6
Napisz w notacji standardowej, a następnie opracuj numer: Dwadzieścia -trzy miliard dwustu pięćdziesiąt milionów pięćset dwudziestu sześcioretek trzysta dwudziestu pięciu z trzema dwudziestoma trzema tysięcznymi.
Rozwiązanie:
Należy pamiętać, że Millardo jest równoważnym miliardem. Słowo Millardo Został zaakceptowany przez Royal Spanish Academy w 1995 r. Na prośbę zmarłego Prezydenta Wenezuelskiego Rafaela Caldera, członka Wenezuelskiej Akademii Języka. W takim przypadku liczba notacji standardowej jest zapisywana w następujący sposób:
23.2501526.325 023
23 miliardy + 250 milionów + 526 tysięcy + 325 sztuk + 23 tysięcznych.
23 × 10^9 + 250 × 10^6 + 526 × 10^3 + 325 × 10^0 + 23 × 10^-3
Wreszcie postać w rozwiniętej notacji jest napisana:
2 × 10^10 + 3 × 10^9 + 2 × 10^8 + 5 × 10^7 + 0x10^6 + 5 × 10^5 + 2 × 10^4 + 6 × 10^3 + 3 × 10^^ 2 + 2 × 10^1 + 5 × 10^0 + 0x10^-1 + 2 × 10^-2 + 3 × 10^-3.
Bibliografia
- Khan academy. Tabele wartości pozycyjnej. Odzyskane z: jest.Khan academy.org
- Khan academy. Napisz opracowany numer (wideo). Odzyskane z: jest.Khan academy.org
- IFRAH, Geoges (1998): Universal History of Figures. Espasa Calpe s.DO.
- Wikipedia. Notacja pozycyjna. Odzyskane z: jest.Wikipedia.com
- Wikipedia. Millardo. Odzyskane z: jest.Wikipedia.com
- « Struktura tlenku fosforu (V), właściwości, uzyskiwanie, zastosowania, ryzyko
- Struktura fosforanu glinu (alpo4), właściwości, uzyskiwanie, zastosowania »

