Notacja dziesiętna

Frakcja 3/2 napisana w notacji dziesiętnej

Czym jest notacja dziesiętna?

Notacja dziesiętna Polega na napisaniu liczby rzeczywistych przez całą część i części dziesiętną, zarówno oddzielone punktem lub przecinkiem. Cała część jest pozostawiona, a część dziesiętna po prawej stronie tego punktu.

0 może pojawić się zarówno w całej części, jak i po przecinku. Na przykład następujące liczby to liczby dziesiętne:

• 0.25
• 1.5903
• 4 19367

Zauważ, że dziesiętna część tych liczb jest skończona, ale istnieją również liczby z nieskończoną częścią dziesiętną, na przykład 0,33333…, gdzie punkty zawiesinowe są umieszczone jako sposób na wskazanie, że liczba dziesięcioleci trwa w nieskończoność.

Ogólnie rzecz biorąc, skończony numer dziesiętny można zapisać jako:

N.Do₁Do₂Do₃… Do_N

Będąc N Liczbą całkowitą i n ilość dziesiętnych, podczas gdy nieskończona dziesiętna przyjmuje formę:

N.Do₁Do₂Do₃..

W dziesiętnym 0.25 jest zidentyfikowanych:

• N = 0
• Do₁ = 2
• Do₂ = 5

Dziesiętne powstają jako inny sposób wyrażania racjonalnych liczb, które są kształtowane lub złamane. W rzeczywistości każda ułamek można zapisać w notacji dziesiętnej, co będzie widać natychmiast.

Służą również do reprezentowania liczb, które nie pochodzą z ułamka, SO -CALED Irracjonalne liczby, takie jak: π, √2, √3, √5, liczba „e” i wiele innych.

Przykłady liczb dziesiętnych

Liczbę dziesiętną można uzyskać z ułamka w bardzo prosty sposób: obliczanie ilorazu licznika między mianownikiem. Jeśli mianownik jest jednostką, a następnie zeros, jest to bardzo proste:

• 8/10 = 0.8
• - (5/100) = −0.05

W pierwszym przypadku, ponieważ mianownik wynosi 10, punkt dziesiętny jest umieszczony natychmiast po lewej stronie 8 i dziesiętnej 0.8 czyta „8 dziesiątych” lub „zero punktu ósmego”.

W drugim przypadku, ponieważ mianownik wynosi 100, musisz umieścić punkt dziesiętny dwa miejsca po lewej stronie 5, a ponieważ liczba jest ujemna, odczytuje „mniej 5 setnych” lub „mniej zero zerowego punktu pięć”.

Gdy mianownik nie jest jednostką, a następnie 0, używany jest długi podział:

Zauważ, że aby przeprowadzić ten podział, ponieważ licznik jest mniejszy niż mianownik, został on pomnożony najpierw przez 10, a tym samym, 0, a następnie punkt dziesiętny w ilorazie, aby nie zmieniać operacji, tak nie Aby zmienić operację. Następnie przejdź normalnie, aby podzielić 10 przez 2, które wynosi 5, a pozostałość podziału wynosi 0.

Może ci służyć: kwoty wektorowe

Dziesiętna forma ułamka ½ wynosi 0.5, ten „Zero Point Five” jest czytany:

Frakcja 7/8 to kolejny przykład. Ponieważ 7 jest mniej niż 8, mnoży 7 × 10 = 70, A 0 jest umieszczany w ilorazie, a następnie punkt dziesiętny i zwykle jest podzielony:

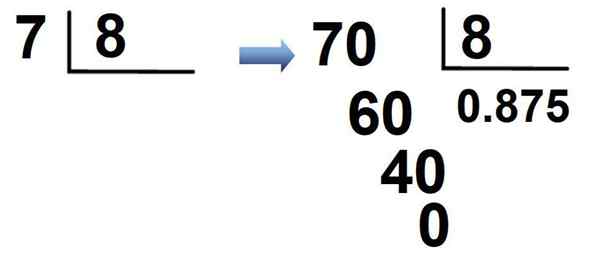
W rezultacie ułamek jest zapisywany w notacji dziesiętnej jako:

7/8 = 0.875

Ta liczba, podobnie jak poprzedni wynik, jest skończoną dziesiętną, a sposobem na odczyt jest: „Zero punktem osiemset siedemdziesiąt lat”. Dzięki tej procedurze następujące ułamki są również zapisane w notacji dziesiętnej:

8/10 = 0.8

5/7 = 0.714285714…

9/20 = 0.Cztery pięć

3/8 = 0.375

Zauważ, że jak we wszystkich tych frakcjach licznik jest mniejszy niż mianownik, cała część powstałych dziesiętnych wynosi 0. Jednak liczba mieszana lub Ułamek niewłaściwy (Ten, którego licznik jest większy niż jego mianownik) ma również reprezentację dziesiętną.

W takim przypadku cała część jest większa lub równa 1, jeśli ułamek jest dodatni i mniej niż -1, jeśli jest ujemny:

9/4 = 2.25

10/3 = 3.333333…

−12/5 = −2.4

1 ½ = 1.5

2 ¾ = 2.75

Cała część i ułamkowa część ujemnych dziesiętnych

W poprzednich przykładach zaobserwowano, że aby znaleźć dziesiętną ekspresję frakcji, licznik i mianownik są po prostu podzielone. Nawet jeśli ułamek jest ujemny, po prostu znak minus jest umieszczony na równoważnym dziesiętnym wyrażeniu.

Jednak cała część i ułamkowa część dziesiętnego różnią się w zależności od znaku, który nosisz.

Kiedy dziesiętne jest pozytywne, jak 2.25, cała jego część to 2, a jej dziesiętna część to 0.25, a liczba może być napisana jako suma całej części i części dziesiętnej, taka:

2.25 = 2 + 0.25

Cała część jest zdefiniowana jako liczba całkowita bezpośrednio niższa niż dziesiętna, a część dziesiętna jest zawsze pozytywna. Dla 2.25, natychmiastowa liczba całkowita wynosi 2.

Ale w przypadku frakcji -12/5, równoważne z dziesiętnym −2.4 Powyższe nie działa.

Może ci służyć: jakie są części płaszczyzny kartezjańskiej?

 Jeśli -2 to była cała część i 0.4 Część dziesiętna, przez dodanie zostanie uzyskane:

−2 + 0.4 = −1.6 ≠ −2.4

Dlatego cała część -2.4 nie może być -2, ale natychmiastowa liczba całkowita: −3. Ale w takim przypadku część ułamkowa nie wynosiłaby 0.4, ponieważ dodając:

−3 + 0.4 = −2.6 ≠ −2.4

Więc jaka jest dziesiętna część liczby ujemnej −2.4? Odejmuje liczbę dziesiętną od całej jego części, a wynik będzie zawsze pozytywny:

−2.4 - ( - 3) = 0.6

Wreszcie, udowodniono, że dodając całą część i część ułamkową, uzyskana jest poszukiwana dziesiętna:

−3 + 0.6 = −2.4

Procedura znalezienia całej części i dziesiętnej części dowolnej liczby, niezależnie od znaku, jest podsumowana w ten sposób:

• Cała część jest liczbą całkowitą bezpośrednio niższą niż liczba dziesiętna.
• Część dziesiętna jest obliczana przez odjęcie dziesiętnego od całej części.

Jednak w celach kalkulacji praktycznych liczba dziesiętna -2.4 można rozbić jako - (2 + 0.4) = - 24/10 lub:

Jak widać, reprezentacja notacji dziesiętnej liczby nie jest wyjątkowa.

Rodzaje dziesiętnych

Istnieją liczby dziesiętne, których część dziesiętna jest skończona lub nieskończona, która jest wykorzystywana jako kryteria klasyfikacji:

Skończone lub dokładne dziesiętne

Kiedy dziesiętne są skończone, na przykład 0.125, mówi się również, że są Dokładne dziesiętne.

Nieskończone dziesiętne

Nieskończona dziesiętna jest uzyskiwana, gdy pozostałość podziału między licznikiem a mianownikiem nigdy nie jest wykonana 0.

Pod warunkiem, że dziesiętna pochodzi z ilorazu dwóch liczb całkowitych, ta dziesiętna część jest okresowa, to znaczy składa się z jednej lub kilku postaci, które są powtarzane w nieskończoność, nazywane okres.

Na przykład numer 3.333333… powstały przez niewłaściwą frakcję 10/3, jest to okresowa dziesiętna: cała część to 3, a po punkcie dziesiętnym liczba 3 jest powtarzana w nieskończoność. Można to symbolizować, umieszczając krzywą lub czapkę na powtarzanej liczbie:

Okres może być większą liczbą, jak w ułamku 5/7, którego reprezentacja w notacji dziesiętnej wynosi 0.71428571428571428… i jest napisane jako:

Może ci służyć: proporcjonalna różnica

Te dziesiętne, w których okres pojawia się natychmiast po wywołaniu punktu dziesiętnego Czyste okresowe dziesiętne. Jednak w tym drugim:

Okres, który wynosi 45, jest poprzedzony dwoma cyframi, które nie są już powtarzane w części dziesiętnej: 23. Ta liczba jest nazywana Ante-okres, Ponieważ poprzedza okres. W tym przypadku jest to Mieszana gazeta dziesiętna.

Wreszcie istnieją nieskończone dziesiętne dziesiętne, które nie są gazetami, które nie pochodzą z ilorazu między dwiema liczbami. Jak wspomniano na początku, te dziesiętne należą do całości Irracjonalne liczby, Na przykład podobnie jak numer PI.

Rozwiązane ćwiczenia

Ćwiczenie 1

Napisz numeryczne następujące liczby dziesiętne:

a) Zero punktu czterysta czterdzieści lat
b) pięć tysięcznych
c) dwie jednostki i pięć setnych
d) Trzy punkty dwadzieścia -siedem negatywnych
e) Jeden punkt osiemset dwadzieścia tysięcy pięćset sześćdziesiąt -trzy

• Rozwiązanie

a) 0.447

b) 0.005

c) 2.05

d) −3.27

e) 1.824563

Ćwiczenie 2

Klasyfikuj następujące liczby dziesiętne w dokładnej dziesiętnej, czyste gazety, mieszane gazety lub liczby irracjonalne. We wszystkich przypadkach wskaż wartość całej części, a jeśli są to gazety lub gazety mieszane, wskaż również wartość okresu i przednie, odpowiednio:

a) 0.35627

b) 1.21212121…

c) −1.32

d) 1.414213562… = √2

• Rozwiązanie

a) 35627 jest dokładnym dziesiętnym. Cała jego część to 0, a część dziesiętna wynosi 0.35627.

b) 1.21212121… jest nieskończoną gazetą dziesiętną i czystą, cała część to 1, a okres to 21.

c) −1.32 jest dokładnym i ujemnym dziesiętnym, którego cała część wynosi -2. Część dziesiętna jest obliczana przez odjęcie liczby dziesiętnej od całej części:

−1.32 - (−2) = 0.68

d) dziesiętna ekspresja √2 jest nieskończona i nie okresowa, ponieważ jest to liczba irracjonalna.

Jest to mieszana gazeta, cała część to 3, przednia wynosi 1, a okres to 89.

Bibliografia

1. Wkład pedagogiczny i materiał dydaktyczny. Notacja dziesiętna. Odzyskane z: tecdigital.Tec.AC.Cr.
2. Baldor, a. 2007. Praktyczna arytmetyka teoretyczna. Grupa redakcyjna Patria S.DO. c.V.
3. Matematyka dla transakcji. Zrozumienie notacji dziesiętnej. Źródło: openTextBC.AC.
4. Unam. Liczby racjonalne: znaczenia i reprezentacje. Odzyskane z: Redi.Kodeks.Unam.MX.