Matematyka

Kąty i trójkąty

Kąty i trójkąty
Kąty i trójkąty są częścią płaskiej geometrii. Shuttersock

Jakie są kąty i trójkąty?

A kąt Jest to region samolotu wyznaczony przez dwa półprzestrzenne z punktem pochodzenia wspólnego. Ten punkt jest znany jako wierzchołek, podczas gdy nazywane są półstaight boki. Z drugiej strony a trójkąt Jest to liczba trzech kąty i trzech stron, z trzema wierzchołkami.

Najpierw porozmawiamy o kątach.

Kąty

Istnieje kilka sposobów oznaczenia kątów: poprzez greckie litery, takie jak α, β, γ, do których można dodać akcent obwodowy; z literami kapitałowymi tapicerowanymi lub małymi literami, A, B, C, A, B, C; Liczby, takie jak 1, 2, 3 ... lub za pomocą symbolu kątowego ∠.

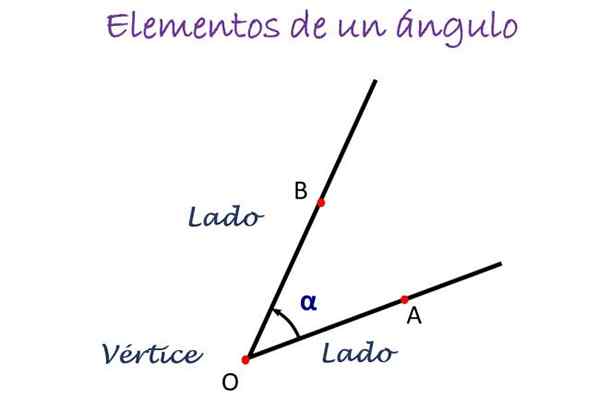Główne elementy kąta. Źródło: f. Zapata

Na powyższym rysunku kąt jest mierzony z boku A do B, wskazany przez kierunek strzałki, a na środku litera oznaczająca wierzchołek jest umieszczany, który jest normalnie lub. Kąt jest następnie oznaczony jako ∠ AOB.

Gdy kąt jest mierzony w sensie przeciwhorarium, znak A +jest dowolnie przypisywany, a jeśli jest mierzony w harmonogramie, znak -aby je rozróżnić.

Miara kątów jest przeprowadzana za pomocą transportera, który składa się z półkolistego arkusza z tworzywa sztucznego, takiego jak ten pokazany poniżej. Półkola jest podzielona na 180 równych części, każde połączenie stopień.

Aby zmierzyć, wierzchołek kąta jest zbieżny z centralnym punktem transportera, wskazanego z strzałką, a początkową stroną z jedną z krawędzi, wewnętrznych lub zewnętrznych. Ostateczna strona przecina niektóre znaki transportera, a miara ta jest kątem.

Może ci służyć: reguła empiryczna: jak to zastosować, po co to jest rozwiązane ćwiczenia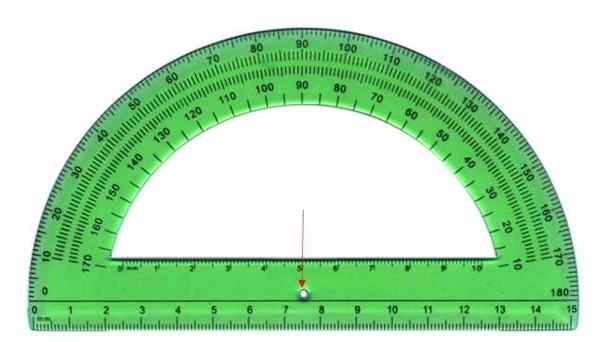Przenośnik jest instrumentem do pomiaru kąta. Źródło: Wikimedia Commons

Rodzaje kątów

Jednym z najczęściej używanych kryteriów do klasyfikacji kątów jest zgodnie z jego miarą. Dlatego kąt może być:

  • Zero, mierzy 0º.
  • Ostry, którego miara wynosi od 0 do 90º.
  • Prosty, Mierzy dokładnie 90º.
  • Rozwarty, Jest większy niż 90º i mniej niż 180º.
  • Płaski, Jego miara wynosi 180º.
  • Kompletny, reprezentuje całkowity obrót i mierzy 360º.
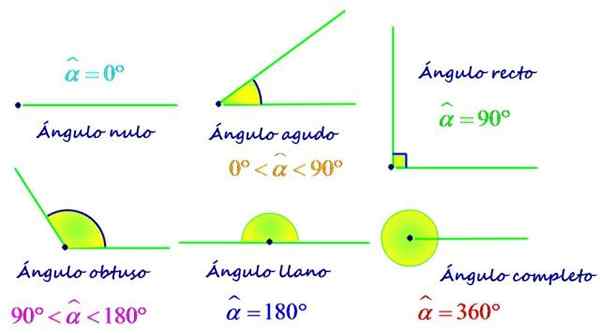Rodzaje kątów zgodnie z twoją miarą. Źródło: f. Zapata.

Zgodnie z związek między jej miarą a płaskim kątem, który wynosi 180º, kąty można również sklasyfikować jako:

  • Wklęsły, Jeśli mierzy mniej niż 180º. Dlatego ostre, proste i tępe kąty są wklęsłe, ponieważ jego miara jest zawsze mniejsza niż 180º (patrz powyższy rysunek).
  • Wypukły, Jeśli twoja miara jest większa niż 180º, ponieważ kąty 270º i 360º.

Kąty zgodnie z sumą ich miar i zgodnie z pozycją ich boków

Dwa kąty ∠ A i ∠ B mogą być:

  • Uzupełniający, Jeśli suma jego miar jest równa 90º.
  • Uzupełniający, Podczas dodawania odpowiednich miar uzyskuje się 180º.
  • Skoniugowany, Jeśli ta suma jest równa 360º.
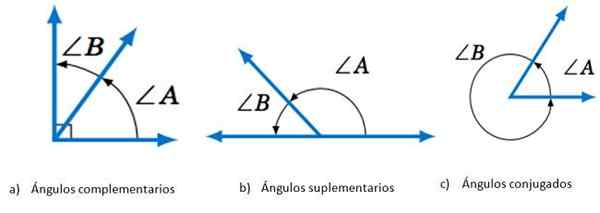Kąty zgodnie z sumą jego miar. Źródło: Mathematics Librettexts.

Jeśli chodzi o pozycję ich boków, mogą być dwa kąty:

  • Z rzędu, Kiedy wierzchołek i jedna z boków ma wspólnego.
  • Przylegający, Jeśli są one kolejne, ale niezgodne strony są przeciwne, więc są również uzupełniające.
  • Przeciwnie przez wierzchołek, Kiedy mają wspólny wierzchołek, a boki kąta są przedłużone w przeciwnym kierunku.
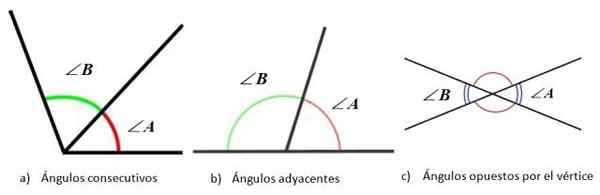Kąty zgodnie z względną pozycją między jej stronami. Źródło: f. Zapata

Trójkąty

Trójkąt jest płaską i zamkniętą postacią geometryczną, należącą do rodziny wielokątów, z trzema bokami składającymi się z linii, które są wycięte od dwóch do dwóch, generując trzy kąty.

Może ci służyć: funkcja bijkłowców: co to jest, jak to się dzieje, przykłady, ćwiczenia

Jego podstawowe elementy to:

  • Wierzchołki, które są punktami przecięcia wyżej wymienionych linii.
  • boki, w sumie 3 i które składają się z segmentów linii łączących się z wierzchołkami.
  • Kąty wewnętrzne, Również w liczbie 3, których suma jest zawsze równa 180º.

Zasadniczo boki są oznaczone małymi literami łacińskimi, wierzchołki z literami kapitałowymi i kątami z małymi literami grrieous, ale inne notacje są również możliwe.

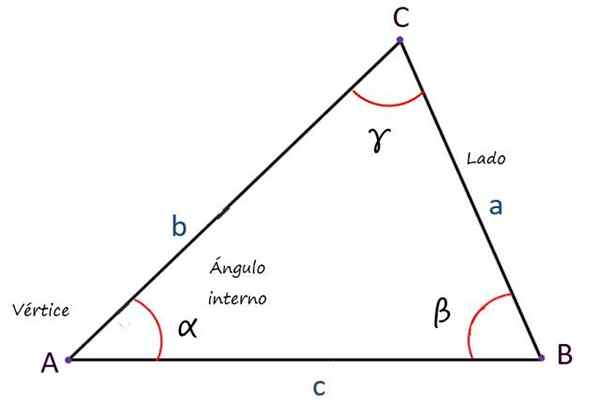Główne elementy trójkąta. Źródło: f. Zapata

Rodzaje trójkątów

Trójkąty zgodnie z kształtem jego boków

Zgodnie z tym kryterium trójkąty mogą być:

  • Równoboje, Jeśli jego trzy strony mają tę samą miarę.
  • Równoramienny, Gdy tylko dwie strony mają równą miarę, podczas gdy trzecia jest inna.
  • Różnoboczny, Jeśli trzy boki mają inny rozmiar.
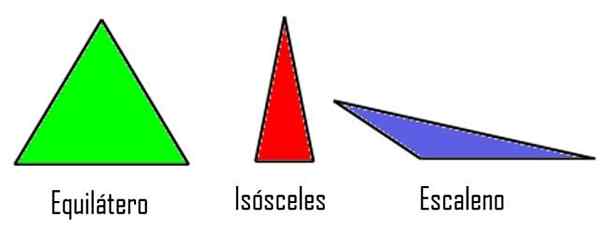Trójkąty według ich boków. Zmodyfikowana wikimedia Commons

Trójkąty zgodnie z jego wewnętrznymi kątami

Kryterium to oparte jest na wewnętrznych typach kątów trójkąta. Zgodnie z tym może być trójkąt:

  • Acutangle, Gdy trzy wewnętrzne kąty trójkąta są ostre.
  • Prostokąt, Jeśli trójkąt ma wewnętrzny kąt miary równy 90º.
  • Rozwarty, Jeden z wewnętrznych kątów trójkąta jest tępy.
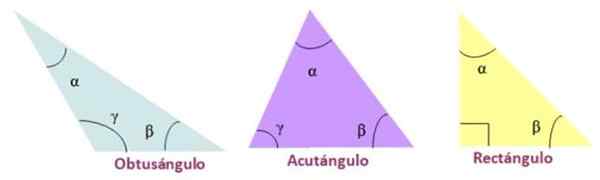Rodzaje trójkąta zgodnie z jego wewnętrznymi kątami. Źródło: f. Zapata

Godne uwagi segmenty trójkąta

Wśród godnych uwagi segmentów każdego trójkąta mają:

  • Mediana, segment skierowany z wierzchołka, bezpośrednio na przeciwną stronę.
  • Pośredniczka, Jest to segment należący do linii prostopadłej do boku, który przecina się do punktu środkowego tej strony.
  • Dwusieczna, segment, który dzieli kąt wewnętrzny na dwie równe części i rozciąga się na przeciwną stronę do kąta.
  • Wysokość, segment prostopadły do ​​boku, który rozciąga się na przeciwny wierzchołek.
Może ci służyć: interpolacja Lagrange

Trzy średnie, trzy mediary można prześledzić i tak dalej.

Centra trójkąta

W każdym trójkącie wyróżniają się następujące punkty (patrz następujący rysunek):

  • Barcentro g, czasami nazywane Centroid trójkąta jest to punkt przecięcia median i zawsze jest wewnętrzny wobec trójkąta.
  • Ortocenter h, punkt, w którym przecinają się trzy wysokości.
  • Circcentro lub, Jest to punkt przecięcia mediów. Można go znaleźć poza trójkątem, jeśli jest to tępe, podczas gdy w trójkącie prostokąta lub pokrywa się z punktem środkowym hipotenu.
  • W centrum, punkt przecięcia dla trójkątnych bisektorów.
  • Euler prosto, prosto, który łączy barycenter, ortocenter i obwód, w każdym trójkącie, który nie jest równoboczny. Zawsze spełnia się, że długość segmentu HG jest dwukrotnie więcej niż w segmencie Go.
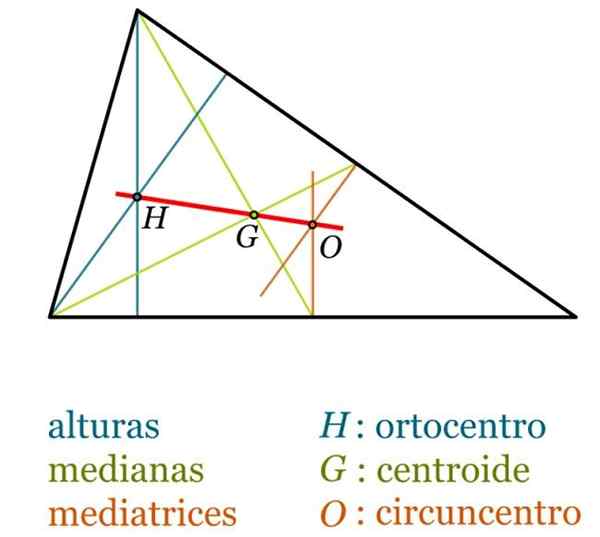Godne uwagi punkty i segmenty trójkąta. Źródło: Wikimedia Commons

Obszar trójkąta

Aby obliczyć obszar A trójkąta, stosuje się następujący formuła o charakterze ogólnym:

A = podstawa × wysokość / 2

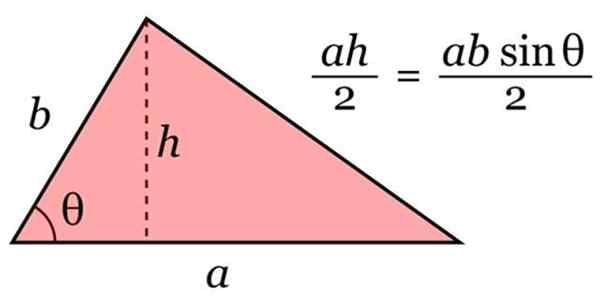Obszar trójkąta. Źródło: Wikimedia Commons

Formuła Herón

Znając długość wszystkich stron trójkąta, następująca formuła, znana jako Formuła Herón, Pozwala znaleźć obszar A:

Tutaj boki trójkąta to A, B i C, podczas gdy SP czy on jest Perymetr półprzewodnikowy, to znaczy połowa obwodu p = a + b + c.

Bibliografia

  1. Alexander, zm. 2013. Geometria. 5. Wydanie. Cengage Learning.
  2. Kąty. Mathematics Librettexts. Odzyskane z: matematyki.Librettexts.org.
  3. Jiménez, René. 2010. Matematyka II (geometria i trygonometria). 2. Wydanie. osoba.
  4. Formuły wszechświata. Trójkąt. Odzyskane z: Universoformulas.com.
  5. Zapata, f. Trójkąty: historia, elementy, klasyfikacja, właściwości. Pobrano z: Lifer.com.